二叉树

约 1485 个字 240 行代码 5 张图片预计阅读时间 8 分钟总阅读量次

101 对称二叉树

二叉树｜迭代 + 递归

🔑🔑 难度：Easy 简单

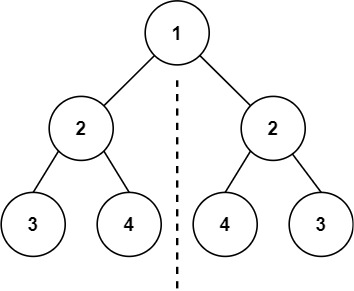
示例1: 给你一个二叉树的根节点 root ，检查它是否轴对称。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import deque
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        queue = deque()
        queue.append(root)
        while queue:
            length = len(queue)
            cur_num = []
            for i in range(length):
                cur = queue.popleft()

                if cur.left:
                    queue.append(cur.left)
                    cur_num.append(cur.left.val)
                else:
                    cur_num.append(-101)
                if cur.right:
                    queue.append(cur.right)
                    cur_num.append(cur.right.val)
                else:
                    cur_num.append(-101)
            # print(cur_num)
            if cur_num != list(reversed(cur_num)):
                return False
        return True

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import deque
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:

        def check(p, q):
            if p == None and q == None:
                return True
            if p == None or q == None:
                return False
            return p.val == q.val and check(p.left, q.right) and check(p.right, q.left)
        return check(root.left, root.right)

迭代的做法，每一层看看是否对称，需要一个队列；

递归的做法，：它们的两个根结点具有相同的值，每个树的右子树都与另一个树的左子树镜像对称

我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树，\(p\) 指针和 \(q\) 指针一开始都指向这棵树的根，随后 \(p\) 右移时，\(q\) 左移，\(p\) 左移时，\(q\) 右移。每次检查当前 \(p\) 和 \(q\) 节点的值是否相等，如果相等再判断左右子树是否对称。

437. 路径总和 III

定义子函数

🔑🔑 难度：Medium 中等

示例1: 给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出：3 解释：和等于 8 的路径有 3 条，如图所示。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:

        def rootSum(root, target):
            if root == None:
                return 0
            cnt = 0
            if root.val == target:
                cnt += 1
            cnt += rootSum(root.left, target - root.val)
            cnt += rootSum(root.right, target - root.val)
            return cnt

        if root is None:
            return 0
        rv = rootSum(root, targetSum)
        riv = self.pathSum(root.right, targetSum)
        lev = self.pathSum(root.left, targetSum)
        return rv + riv + lev

注意，最终结果的来源具体有：包含root，同时从root向右；包含root，同时从root向左；不包含root，此时就是递归了，分别检查左右各有几个。所以有一个函数要单独实现：包含root的路径搜寻。（对应上面的rootSum函数）

124. 二叉树的最大路径和

🔑🔑 难度：High 困难

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.maxValue = float('-inf')

        def dfs(head):
            if not head:
                return 0
            max_l = max(0, dfs(head.left))
            max_r = max(0, dfs(head.right))
            self.maxValue = max(self.maxValue,  max_l + max_r + head.val)
            return max(max_l, max_r) + head.val

        dfs(root)
        return self.maxValue

dfs(head) 返回的结果是“包含head的路径的最大值，因此，由两部分组成：左边的最大，右边的最大，加上自己。而每次递归的时候，都去判断一下，是否可以更新当前的value。而正因为是包含head的路径的最大值，所以这个函数本身返回的值，必须包括自己，剩下的，捡左右两边最大的（没有的话就都不选）。

105. 从先序和中序遍历构造二叉树

十分经典的递归：截断位置。

🔑🔑 难度：Medium 中等

示例1: 给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

输出: [3,9,20,null,null,15,7]

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if len(inorder) == 0:
            return None
        cut = 0
        for i in range(len(inorder)):
            if inorder[i] == preorder[0]:
                cut = i


        root = TreeNode(preorder[0])
        root.left = self.buildTree(preorder[1: cut + 1], inorder[:cut])
        root.right = self.buildTree(preorder[cut + 1: ], inorder[cut + 1: ])
        return root

226. 翻转二叉树

🔑🔑 难度：Easy 简单

示例1:

输入：root = [4,2,7,1,3,6,9]

输出：[4,7,2,9,6,3,1]

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if root == None:
            return None
        right = self.invertTree(root.right)
        left = self.invertTree(root.left)
        root.left = right
        root.right = left
        return root

208. 实现前缀树

🔑🔑 难度：Medium 中等

Trie（发音类似 "try"）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补全和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入 "Trie", "insert", "search", "search", "startsWith", "insert", "search"] [], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]] 输出 null, null, true, false, true, null, true]

解释 rie trie = new Trie(); rie.insert("apple"); rie.search("apple"); // 返回 True rie.search("app"); // 返回 False rie.startsWith("app"); // 返回 True rie.insert("app"); rie.search("app"); // 返回 True

class Trie:

    def __init__(self):
        self.children = [None] * 26
        self.isEnd = False

    def insert(self, word: str) -> None:
        node = self
        for ch in word:
            ch_ = ord(ch) - ord('a')
            if not node.children[ch_]:
                node.children[ch_] = Trie()
            node = node.children[ch_]
        node.isEnd = True

    def searchPrefix(self, prefix):
        node = self
        for ch in prefix:
            ch_  = ord(ch) - ord('a')
            if node.children[ch_] == None:
                return None 
            node = node.children[ch_]
        return node 

    def search(self, word: str) -> bool:
        node = self.searchPrefix(word)
        return node is not None and node.isEnd

    def startsWith(self, prefix: str) -> bool:
        return self.searchPrefix(prefix) is not None
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)

这里注意，我们的每个children 都是一个Trie类，构成一个大树。还需要注意，由于需要查找特定结尾的字符串是否在这个树中，所以需要添加 isEnd 属性，不然插入 'apple'，会发现 'app' 这个词也能查找到，但是实际上这只是一个前缀；第三，注意我们自己实现了 searchPrefix 这个方法用来查找前缀。

543. 二叉树的直径

🔑🔑 难度：Medium 中等

输入：root = [1,2,3,4,5]

输出：3

解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:

        self.maxVal = 0
        def dfs(head):
            if not head:
                return -1
            L = dfs(head.left) + 1
            R = dfs(head.right) + 1
            self.maxVal = max(self.maxVal, L + R )
            return max(L, R) 
        dfs(root)
        return self.maxVal

可以记模板：到当前节点为止，其直径是其左侧的链条长 + 右侧的链条长，左侧链条如果为None，则需要返回0，而以该节点为孩子的父节点，其长度为该节点左右最长链条里选择一个。

230. 二叉搜索树中的第K小元素

🔑🔑 难度：Medium 中等

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        self.K = k 
        self.result = 0

        def dfs(head):
            if not head:
                return 

            if self.K == 0:
                return 

            dfs(head.left)
            self.K -= 1
            if self.K == 0:
                self.result = head.val 
                return 
            dfs(head.right)

        dfs(root)
        return self.result

模板题：二叉搜索树的中序遍历就是一个排序的数组，所以直接中序遍历，但是记录当前是“倒数第几个”，直到某次减为0

114. 二叉树展开为链表

🔑🔑 难度：Medium 中等

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。展开后的单链表应该与二叉树先序遍历顺序相同。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        result = []
        def preorder(head):
            if not head:
                return 
            result.append(head)
            preorder(head.left)
            preorder(head.right)
        preorder(root)
        for idx, node in enumerate(result):
            if idx == len(result) - 1:
                node.left = None 
                node.right = None 
            else:
                node.left = None 
                node.right = result[idx + 1]

先过一遍先序遍历，然后根据这个顺序，重新连接二叉树的节点。