双指针 / 滑动窗口

约 1875 个字 181 行代码 1 张图片 预计阅读时间 9 分钟 总阅读量 次

11. 盛最多水的容器

两边向中间夹逼

🔑🔑 难度：Medium 中等

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例1: 输入：[1,8,6,2,5,4,8,3,7]

输出：49

解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area = 0
        l , r = 0, len(height) - 1
        while l < r:
            max_area = max(max_area , min(height[l], height[r]) * (r - l))
            if height[l] <= height[r]:
                l += 1
            else:
                r -= 1
        return max_area

为什么可以两边向中间夹，每次只需要移动更小的指针 ：因为随着指针移动，能用来装水的范围只会越来越小，所以，就算移动最大的指针，找到的结果不会比现在的这个解更大的。

---

15. 三数之和

双指针

🔑🔑 难度：Medium 中等

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例1: 示例 1： 输入：nums = [-1,0,1,2,-1,-4]

输出：[[-1,-1,2],[-1,0,1]]

解释： nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0

nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0

nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。

不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。

注意，输出的顺序和三元组的顺序并不重要。

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        result = []
        nums = sorted(nums)
        for i in range(len(nums) - 2):
            if i > 0 and nums[i] == nums[i - 1]:
                continue
            l , r = i + 1, len(nums) - 1
            while l < r:
                if nums[i] + nums[l] + nums[r] > 0:
                    r -= 1
                elif nums[i] + nums[l] + nums[r] < 0:
                    l += 1
                else:
                    result.append([nums[i] , nums[l],  nums[r]])
                    l += 1
                    r -= 1
                    while l < r and nums[l] == nums[l - 1]:
                        l += 1
                    while r > l and nums[r] == nums[r + 1]:
                        r -= 1

        return result

官方做法：

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        nums.sort()
        result = []

        for first in range(n):
            if first > 0 and nums[first] == nums[first - 1]:
                continue
            third = n - 1
            target = -nums[first]
            for second in range(first + 1, n):
                if second > first + 1 and nums[second] == nums[second - 1]:
                    continue
                while third > second and nums[second] + nums[third] > target:
                    third -= 1
                if third == second:
                    break
                if nums[second] + nums[third] == target:
                    result.append([nums[first], nums[second], nums[third]])
        return result

官方做法这里注意了，第一个first从头开始走，第二个second从first的下一个开始走，第三个third从尾部开始走。需要处理重复的元素

思路要清楚：先排序，然后双指针。双指针写的时候有个小技巧。就是用一个for循环充当第一个指针，然后在遍历过程中用另外的变量记录另一个（或另外几个）变量的位置。这个问题因为不允许重复，所以必须要对相同的元素进行消重。消重的时候为了避免不知道怎么处理，可以每次都把指针自增/自减1，然后判断加了之后是否会和加了之前的重复。见6～7行，见16～17行。也就是，消重的时候尽量按照 i != i - 1 的思路来写。

---

56. 合并区间

🔑🔑 难度：Medium 中等

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]

输出：[[1,6],[8,10],[15,18]]

解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key = lambda x: x[0])
        l = intervals[0][0]
        r = intervals[0][1]
        result = []
        n = len(intervals)
        for idx, (a,b) in enumerate(intervals):
            if a > r:
                result.append([l, r])
                l = a
                r = b
            else:
                r = max(r, b)

            if idx == n - 1:
                result.append([l, r])
        return result

先排序，后合并，始终维护“当前的最左边”和“当前的最右边”。注意右侧项变化的逻辑：max(r, b)

---

283. 移动0

双指针的典型题

🔑🔑 难度：Easy 简单

示例1: 给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1

输入: nums = [0,1,0,3,12] 输出: [1,3,12,0,0]

示例 2: 输入: nums = [0]

输出: [0]

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        left = right = 0
        n = len(nums)
        while right < n:
            if nums[right] != 0:
                nums[left] , nums[right]  = nums[right], nums[left] 
                left += 1
            right += 1

动得更快的是right，检测哪边是非0的，left是保证“在我之前的数字都是非0了”。

---

🌟42. 接雨水

🔑🔑 难度：High 困难

示例1: 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出：6

解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0
        n = len(height)
        leftMax = [0 for _ in range(n)]
        rightMax = [0 for _ in range(n)]
        for i in range(n ):
            if i == 0:
                leftMax[i] = height[i]
            else:
                leftMax[i] = max(height[i], leftMax[i - 1])
        for i in range(n - 1, - 1, -1):
            if i == n - 1:
                rightMax[i] = height[i]
            else:
                rightMax[i] = max(height[i], rightMax[i + 1])
        # print(rightMax, leftMax)
        res = 0
        for i in range(n):
            res += (min(leftMax[i], rightMax[i]) - height[i])
        return res

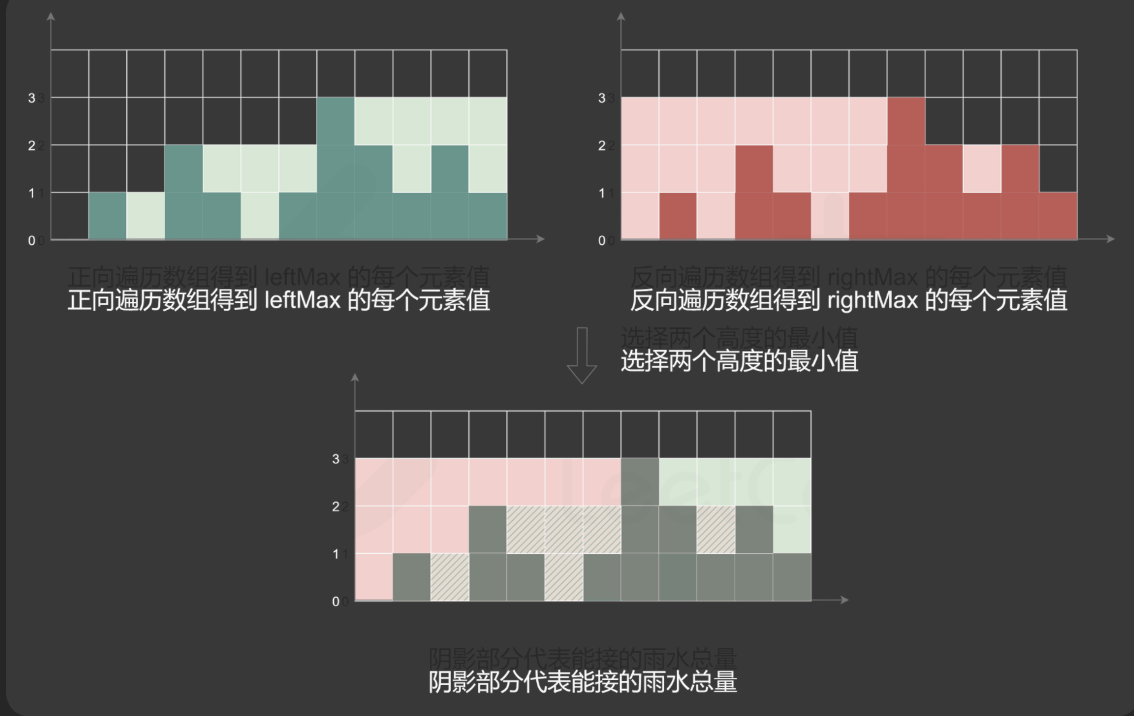
分别记录左边最高的位置和右边最高的位置，取最小值，减去当前位置原本的高度即可。

---

以下为滑动窗口部分的题目

438. 找到字符串中所有字母异位词

🔑🔑 难度：Medium 中等

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

示例 1:

输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。 示例 2:

输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

class Solution:
    def findAnagrams(self, s: str, p: str) -> List[int]:

        result = []
        m = len(s)
        n = len(p)
        if m < n:
            return result
        cnt_s = [0 for _ in range(26)]
        cnt_p = [0 for _ in range(26)]
        for i in range(n):
            cnt_s[ord(s[i]) - ord('a')] += 1
            cnt_p[ord(p[i]) - ord('a')] += 1

        if cnt_s == cnt_p:
            result.append(0)
        for i in range(n, m):
            cnt_s[ord(s[i]) - ord('a')] += 1
            cnt_s[ord(s[i - n]) - ord('a')] -= 1
            if cnt_s == cnt_p:
                result.append(i - n + 1)
        return result

注意，判别两个列表是否完全相同，可以直接用等于号！同时，每次动一个字母，删去前面的，新增保留后面的，与目标做对比。

209. 长度最小的子数组

🔑🔑 难度：Medium 中等

给定一个含有 n 个正整数的数组和一个正整数target` 。

找出该数组中满足其总和大于等于 target 的长度最小的 子数组[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]

输出：2

解释：子数组 [4,3] 是该条件下的长度最小的子数组。

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        l = 0
        r = 0
        sum_inside = 0
        res = len(nums)
        for i in range(len(nums)):
            sum_inside += nums[i]
            if sum_inside < target:
                if i == len(nums) - 1:
                    return 0
                continue
            while l < i and sum_inside - nums[l] >= target:
                sum_inside -= nums[l]
                l += 1
            res = min(res, i - l + 1)


        return res

滑动窗口：始终滑动那个能够满足“ >= target ”的窗口! for循环记录最右侧的位置。

🌟239. 滑动窗口最大值

🔑🔑 难度：High 困难

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3

输出：[3,3,5,5,6,7]

解释：

滑动窗口的位置 最大值 --------------- -----

[1 3 -1] -3 5 3 6 7 -> 3 1 [3 -1 -3] 5 3 6 7 -> 3 1 3 [-1 -3 5] 3 6 7 -> 5 1 3 -1 [-3 5 3] 6 7 -> 5 1 3 -1 -3 [5 3 6] 7 -> 6 1 3 -1 -3 5 [3 6 7] -> 7 示例 2：

输入：nums = [1], k = 1 输出：[1]

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        queue = deque()
        result = []
        for idx, num in enumerate(nums):
            if queue and idx - k == queue[0]:
                queue.popleft()

            while queue and num > nums[queue[-1]]:
                queue.pop()
            queue.append(idx)
            if idx >= k - 1: 
                result.append(nums[queue[0]])
        return result

用一个优先队列进行处理：每当我们向右移动窗口时，我们就可以把一个新的元素放入优先队列中，并保证最上层的元素是所有元素的最大值。如果这个值足够大，那么前面那些小的值就永远不可能出现在滑动窗口中了，我们可以将其永久地从优先队列中移除。以此类推，如果一个新加入的比前面的某些大，那么可以直接取代这些前面的。同样，如果这个元素足够老，那么它会被剔除。

前缀和

🌟560. 和为 K 的子数组

🔑🔑 难度：Medium 中等

示例1:

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        n = len(nums)
        prevSum = [0 for _ in range(n + 1)]
        for i in range(n):
            prevSum[i + 1] = prevSum[i] + nums[i]
        record = defaultdict(int)
        result = 0
        for i in range(n + 1):
            result += record[prevSum[i] - k]
            record[prevSum[i]] += 1
        return result