激活函数⚓︎
约 1705 个字 1 张图片 预计阅读时间 6 分钟 总阅读量 次
首先,回答一个根本问题:为什么需要激活函数?
因为激活函数为神经网络引入了非线性 (non-linearity)。如果没有激活函数,一个无论多深的神经网络,本质上都只是一个复杂的线性变换,其表达能力等同于一个单层网络,无法学习复杂的数据模式。
Why not Sigmoid ?⚓︎
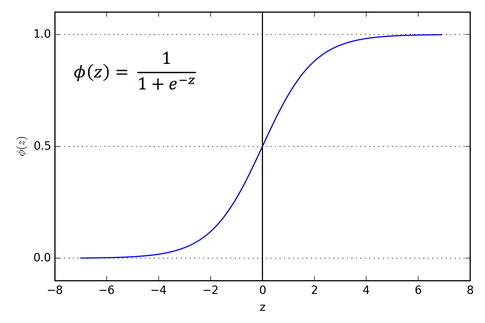
Sigmoid 函数,数学形式为 \(f(x) = \frac{1}{1+e^{-x}}\),曾是神经网络的标配。但它有几个致命的缺陷,导致它在现代深度网络的隐藏层中几乎被完全弃用。
-
梯度消失 (Vanishing Gradients):这是最主要的原因。从上图可以看到,当输入值非常大或非常小时,Sigmoid 函数的曲线变得非常平坦,其导数(梯度)趋近于0。在反向传播过程中,梯度会通过链式法则连乘。如果网络很深,很多层的梯度都小于1,连乘之后梯度会迅速缩小,导致靠近输入层的网络几乎无法得到更新,这就是梯度消失。
-
输出不是零中心 (Not Zero-centered):Sigmoid 的输出恒在 (0, 1) 之间,永远是正数。这意味着传递给下一层的梯度也永远是同号的(要么全为正,要么全为负)。这会导致权重更新时出现“Z字形”的低效更新路径,影响收敛速度。
-
计算成本高:其表达式中包含指数函数
exp(-x),相对于后来简单的 ReLU 函数,计算上更加耗时。
注意:尽管 Sigmoid 不再用于隐藏层,但它仍在特定场景发光发热: * 输出层:在二元分类任务中,用它将输出值转换为一个 (0, 1) 之间的概率。 * 门控机制:在 GRU、LSTM 或 SwiGLU 等结构的“门”中,用它来生成一个 0 到 1 之间的控制信号,决定信息的通过程度。
1. ReLU (Rectified Linear Unit)⚓︎
- 公式: \(f(x) = \max(0, x)\)
- 核心思想: 简单粗暴的“阈值激活”。输入大于0,则原样输出;输入小于等于0,则直接归零。
- 优势:
- 解决梯度消失:在正数区,ReLU 的导数恒为1。这为梯度创造了一条完美的“高速公路”,梯度可以无衰减地向后传播,从而允许训练非常深的网络。
- 计算极其高效: 只需要一个简单的比较操作,比 Sigmoid 和 tanh 快得多。
- 引入稀疏性: 它会使一部分神经元的输出为0,这导致了网络的稀疏性,在一定程度上起到了正则化的作用,减少了参数间的依赖。
- 缺点:
- Dying ReLU 问题: 如果一个神经元的权重在更新后,使得它对于所有训练样本的输入都为负,那么这个神经元将永远输出0,其梯度也永远为0,它就“死亡”了,再也无法被激活和学习。
- 输出不是零中心: 和 Sigmoid 类似,输出也是非负的。
2. GELU (Gaussian Error Linear Unit)⚓︎
- 公式: \(f(x) = x \cdot \Phi(x)\),其中 \(\Phi(x)\) 是标准正态分布的累积分布函数 (CDF)。
- 核心思想: 这是 BERT、GPT-2/3 等早期 Transformer 模型中广泛使用的激活函数。它不是像 ReLU 那样硬性地“门控”(gate),而是根据输入值的符号和大小,对其进行概率性的随机门控。可以直观地理解为,它给 ReLU 增加了一个平滑的、符合高斯分布的随机门。
- 优势:
- 平滑的 ReLU: GELU 是 ReLU 的一个平滑近似,处处可微,这使得训练过程更加稳定。
- 避免 Dying ReLU: 由于其曲线在负值区不是完全为0,而是有一个平滑的过渡,神经元不容易“死亡”。
- 性能优越: 大量实验表明,在 Transformer 架构中,GELU 的性能通常优于 ReLU。
3. SwiGLU (Swish-Gated Linear Unit)⚓︎
这是目前最前沿、效果最好的激活函数之一,被 PaLM、LLaMA 等顶尖大模型采用。理解它需要分两步:
- Swish: 首先有一个叫 Swish (或 SiLU) 的函数,公式为 \(f(x) = x \cdot \text{sigmoid}(\beta x)\)。它和 GELU 非常相似,也是一个平滑、非单调的函数。
- GLU (Gated Linear Unit): GLU 不是一个简单的激活函数,而是一种激活结构。它将前馈网络层的线性变换分成两个部分,一部分作为“内容”,另一部分通过 Sigmoid 激活后作为“门控”,然后将两者逐元素相乘。
\[\text{GLU}(x, W, V, b, c) = \text{sigmoid}(xW+b) \odot (xV+c)\]
SwiGLU 就是将 GLU 中的门控激活函数从 Sigmoid 换成了 Swish。在 LLaMA 等模型的 FFN (前馈网络) 中,其结构变为:
- 输入 \(x\)
- 计算门控值: \(\text{Swish}(x W_1)\)
- 计算内容值: \(x W_2\)
-
最终输出: \(\text{Swish}(x W_1) \odot (x W_2)\) (\(\odot\) 表示逐元素相乘)
-
核心思想: SwiGLU 引入了一个数据驱动的门控机制。传统的激活函数(如ReLU/GELU)是对每个神经元应用一个固定的非线性变换。而 SwiGLU 使用输入 \(x\) 的一部分 (\(x W_2\)) 来动态地、逐元素地决定另一部分 (\(x W_1\)) 中哪些信息应该通过。这个“门”是动态学习的,而不是固定的。
- 优势:
- 表达能力更强: 动态门控机制使得网络可以根据输入内容,自适应地调整激活的强度,具有更强的表达和建模能力。
- 性能登顶: 在众多大模型实验中,基于 SwiGLU 的 FFN 结构显著优于使用 ReLU 或 GELU 的 FFN。
- 缺点:
- 参数量增加: 标准的 FFN 只有一个权重矩阵。而 SwiGLU 结构需要两个(
W1和W2),这会增加 FFN 层的参数量。为了保持总参数量不变,LLaMA 等模型选择将 FFN 的隐藏层维度减少了约 1/3 (从4d降为(2/3)*4d)。
- 参数量增加: 标准的 FFN 只有一个权重矩阵。而 SwiGLU 结构需要两个(
总结对比⚓︎
| 激活函数 | 核心思想 | 优势 | 主要缺点 | 典型应用 |
|---|---|---|---|---|
| Sigmoid | 将值压缩到 (0,1) | 用于概率输出和门控 | 梯度消失、非零中心、计算昂贵 | Logistic 回归输出层、LSTM/GRU门 |
| ReLU | 简单阈值激活 (x > 0) | 无梯度消失(正区)、计算快、引入稀疏性 | Dying ReLU、非零中心 | 经典 CNN、早期深度网络 |
| GELU | 平滑的、概率性的门控 | 平滑、避免Dying ReLU、性能优于ReLU | 计算比ReLU复杂 | BERT, GPT-2, GPT-3 |
| SwiGLU | 数据驱动的动态门控结构 | 表达能力强、性能优异 | 增加FFN层的参数量 | PaLM, LLaMA, Mixtral |
这个演进路径清晰地展示了激活函数从“固定非线性变换”到“动态自适应门控”的发展趋势,这使得模型能够更智能、更灵活地处理和传递信息。