注意力机制:More!⚓︎
约 2765 个字 1 张图片 预计阅读时间 9 分钟 总阅读量 次
因为过于重要所以必须单开一节。不同于 Transformer 一节中大刀阔斧地对整个模型组建的梳理和若干知识点的回答,这一节更加专注于Attention的复杂度、变体以及分析。
自注意力机制的复杂度⚓︎
简单直接的答案是:对于一个长度为 \(n\)、维度为 \(d\) 的输入序列,标准自注意力层的算法复杂度是
\[O(n^2 \cdot d)\]
这个复杂度主要来自于两个矩阵乘法步骤。下面我们来详细分解一下这个计算过程。
为了计算复杂度,我们首先定义几个关键变量:
\(n\):输入序列的长度(即 Token 的数量)。 * \(d\):模型的隐藏层维度(\(d_model\)),也即每个 Token 的 embedding 维度。 * \(d_k\):Query 和 Key 向量的维度。 * \(d_v\):Value 向量的维度。
在经典的 Transformer 实现中,通常有 \(d_k = d_v = d / h\),其中 \(h\) 是注意力头的数量。为了简化分析,我们先假设只有一个头(\(h=1\)),此时 \(d_k = d_v = d\)。
分析⚓︎
我们来回顾一下自注意力的计算公式并分析每一步的计算量。
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]
假设输入矩阵为 \(X\),其维度为 \([n, d]\)。
1. 生成 Q, K, V 矩阵⚓︎
- 操作: 通过将输入矩阵 \(X\) 与三个独立的权重矩阵 \(W_Q\), \(W_K\), \(W_V\) 相乘来生成 \(Q\), \(K\), \(V\)。
- \(Q = X \times W_Q\)
- \(K = X \times W_K\)
- \(V = X \times W_V\)
- 维度分析:
- \(X\): \([n, d]\)
- \(W_Q\), \(W_K\), \(W_V\): \([d, d_k]\) (这里我们假设 \(d_k=d\)) 即 \([d, d]\)
- \(Q\), \(K\), \(V\): \([n, d]\)
- 复杂度: 一次 \([n, d] \times [d, d]\) 矩阵乘法的复杂度是 \(O(n \cdot d \cdot d) = O(n \cdot d^2)\)。由于需要计算三次,总复杂度仍为 \(O(n \cdot d^2)\)。
2. 计算注意力分数 (Scores)⚓︎
- 操作: 计算 \(Q\) 和 \(K\) 的转置的点积。
- \(Scores = Q \times K.T\)
- 维度分析:
- \(Q\): \([n, d]\)
- \(K.T\): \([d, n]\)
- \(Scores\): \([n, n]\)
- 复杂度: \([n, d] \times [d, n]\) 矩阵乘法的复杂度是 \(O(n \cdot d \cdot n) = O(n^2 \cdot d)\)。
- 注意: 后续的缩放操作(除以 \(\sqrt{d_k}\))是逐元素的,其复杂度为 \(O(n^2)\),远小于矩阵乘法,可以忽略不计。
3. Softmax 计算注意力权重⚓︎
- 操作: 对 \(Scores\) 矩阵的每一行应用 Softmax 函数。
- 维度分析:
- \(Scores\): \([n, n]\)
- 复杂度: 对一行 \(n\) 个元素计算 Softmax 的复杂度是 \(O(n)\)。因为有 \(n\) 行,所以总复杂度是 \(O(n^2)\)。
4. 加权求和 V⚓︎
- 操作: 将 Softmax 得到的注意力权重矩阵与 \(V\) 矩阵相乘。
- \(Output = AttentionWeights \times V\)
- 维度分析:
- \(AttentionWeights\): \([n, n]\)
- \(V\): \([n, d]\) (这里我们假设 \(d_v = d\))
- \(Output\): \([n, d]\)
- 复杂度: \([n, n] \times [n, d]\) 矩阵乘法的复杂度是
\[O(n^2 \cdot d)\]
抓大放小⚓︎
现在我们将所有步骤的复杂度放在一起:
- Q,K,V 生成:\(O(n \cdot d^2)\)
- 注意力分数计算:\(O(n^2 \cdot d)\)
- Softmax:\(O(n^2)\)
- 加权求和V:\(O(n^2 \cdot d)\)
在典型的 Transformer 模型中,序列长度 \(n\) (如 512, 1024) 和维度 \(d\) (如 768, 1024) 通常是同一数量级或者 \(d > n\)。但是,序列长度 \(n\) 是可变的,而维度 \(d\) 是固定的超参数。 算法复杂度的分析主要关注随输入规模(即 \(n\))变化的趋势。
最耗时的步骤是第 2 步和第 4 步,它们的复杂度都是 \(O(n^2 \cdot d)\)。因此,整个注意力层的复杂度由这些主导项决定:
总复杂度 = \(O(n \cdot d^2 + n^2 \cdot d)\)
- 当 \(d > n\) 时(例如在处理短文本时),\(n \cdot d^2\) 项可能更大。
- 当 \(n > d\) 时(例如在处理长文档时),\(n^2 \cdot d\) 项会成为绝对的瓶颈。
然而,在算法复杂度的标准表示中,我们通常将这两个维度都视为变量,因此保留这两个项。但在讨论 Transformer 的主要瓶颈时,我们通常特指其对于序列长度 \(n\) 的二次方依赖性,即 \(O(n^2)\) 这一部分。这是因为 \(d\) 是一个固定的模型设计参数,而 \(n\) 是我们希望能够灵活处理的输入长度。
多头注意力 (Multi-Head Attention) 的影响⚓︎
在多头注意力中,维度 \(d\) 被切分成 \(h\) 个头,每个头的维度为 \(d_k = d/h\)。
- 单个头的注意力计算复杂度变为 \(O(n^2 \cdot (d/h))\)。
- 因为 \(h\) 个头是并行计算的,所以总的计算量是 \(h \times O(n^2 \cdot d/h) = O(n^2 \cdot d)\)。
结论:多头注意力机制并不改变整体的渐进复杂度,但它将大的矩阵乘法分解为多个小的矩阵乘法,这种方式更适合现代 GPU 的并行计算,因此在实践中通常更快。
注意力机制的核心瓶颈在于它需要计算一个 \(n \times n\) 大小的注意力分数矩阵。这意味着内存占用和计算量都与序列长度的平方成正比。如果你的输入序列长度翻倍,那么计算和存储注意力矩阵的开销将增长到原来的四倍。这正是限制标准 Transformer 模型处理超长序列(如整本书、高分辨率图像)的主要原因,并催生了如 FlashAttention、稀疏注意力等众多优化算法。
稀疏注意力 (Sparse Attention, GPT-3)⚓︎
Why Sparse?⚓︎
标准的自注意力:
\[
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V
\]
这里的 \(QK^T\) 操作,如果 \(Q\) 和 \(K\) 的维度都是 \((n, d_k)\),\(QK^T\) 的结果就是一个 \((n, n)\) 的矩阵。这就是 \(O(n^2)\) 复杂度的来源。当 \(n\) 很大时(比如,GPT-3 处理的 \(n=2048\) 的序列),这个计算量和内存占用会变得极其巨大。
稀疏注意力的核心思想是:没有必要让每个 token 都去关注(attend to)序列中的其他所有 token。语意信息可能来自于局部的上下文,或者一些具有代表性的、距离较远的 token。因此,我们可以通过==预定义一个稀疏的连接模式,让每个 Query 只与一小部分 Key 进行交互,从而将复杂度降低==。 (Generating Long Sequences with Sparse Transformers, arxiv)
How to "Sparse"?⚓︎
Sparse Attention 并非单一的一种模式,而是几种模式的组合,以近似模拟全连接注意力的信息流动。
主要包含以下几种基础模式:
1. 滑动窗口注意力 (Sliding Window Attention / Local Attention)⚓︎
- 特性与思想: 语言中,一个词的含义最可能由其相邻的词决定。这种模式强制每个 token 只关注其周围一个固定大小(窗口大小为 \(w\))的邻域。
- 操作方法: 对于第 \(i\) 个 token,它只计算与第 \(i-w\) 到第 \(i\) 个 token 之间的注意力分数,也就是在计算 \(QK^T\) 时,注意力矩阵不再是全满的,而是一个 带状矩阵 (band matrix)。第 \(i\) 行只有 \(w\) 个元素是非零的(或者说需要计算的)。
- 复杂度: 时间和空间复杂度都从 \(O(n^2)\) 降低到 \(O(n \cdot w)\)。如果 \(w\) 是一个远小于 \(n\) 的常数,那么复杂度近似为线性 \(O(n)\)。
2. 步进式注意力 (Strided Attention / Dilated Attention)⚓︎
- 特性与思想: 滑动窗口注意力善于捕捉局部信息,但难以捕捉长距离依赖。步进式注意力的灵感来源于空洞卷积(Dilated Convolution),它以固定的步长(stride)跳过一些 token 进行关注。
- 操作方法: 对于第 \(i\) 个 token,它会关注第 \(i-s, i-2s, i-3s, \dots\) 等位置的 token(其中 \(s\) 是步长)。也就是注意力矩阵在每个固定间隔的列上才会有需要计算的值。例如,如果步长为 \(s\),那么第 \(i\) 行只计算第 \(j\) 列,其中 \(j \pmod s = i \pmod s\)。这使得模型可以轻松地访问到距离很远的信息。
- 复杂度: 复杂度为 \(O(n \cdot n/s)\)。
3. 固定式注意力 (Fixed Attention)⚓︎
- 特性与思想: 假设序列中存在一些“全局信息汇总点”,所有 token 都需要参考它们。例如,句子的开头、结尾或者一些特殊的标点符号。
- 操作方法: 预先指定一些固定的位置(例如,每 \(c\) 个 token 的最后几个 token),让序列中所有的 token 都去关注这些固定位置的 token,并且以这个 Token 为截断,前面的文本都不去关注;
- 计算流程: 这种模式下,注意力矩阵的某些列(或某些行)是全满的,而其他地方是稀疏的,并且会以Fixed block的形式进行关注。
最常见的组合是 滑动窗口注意力 + 步进式注意力。这样,每个 token * 既能通过 滑动窗口 关注到紧邻的上下文(捕捉局部细节)。 * 又能通过 步进式 关注到遥远的、有代表性的上下文(捕捉全局依赖)。
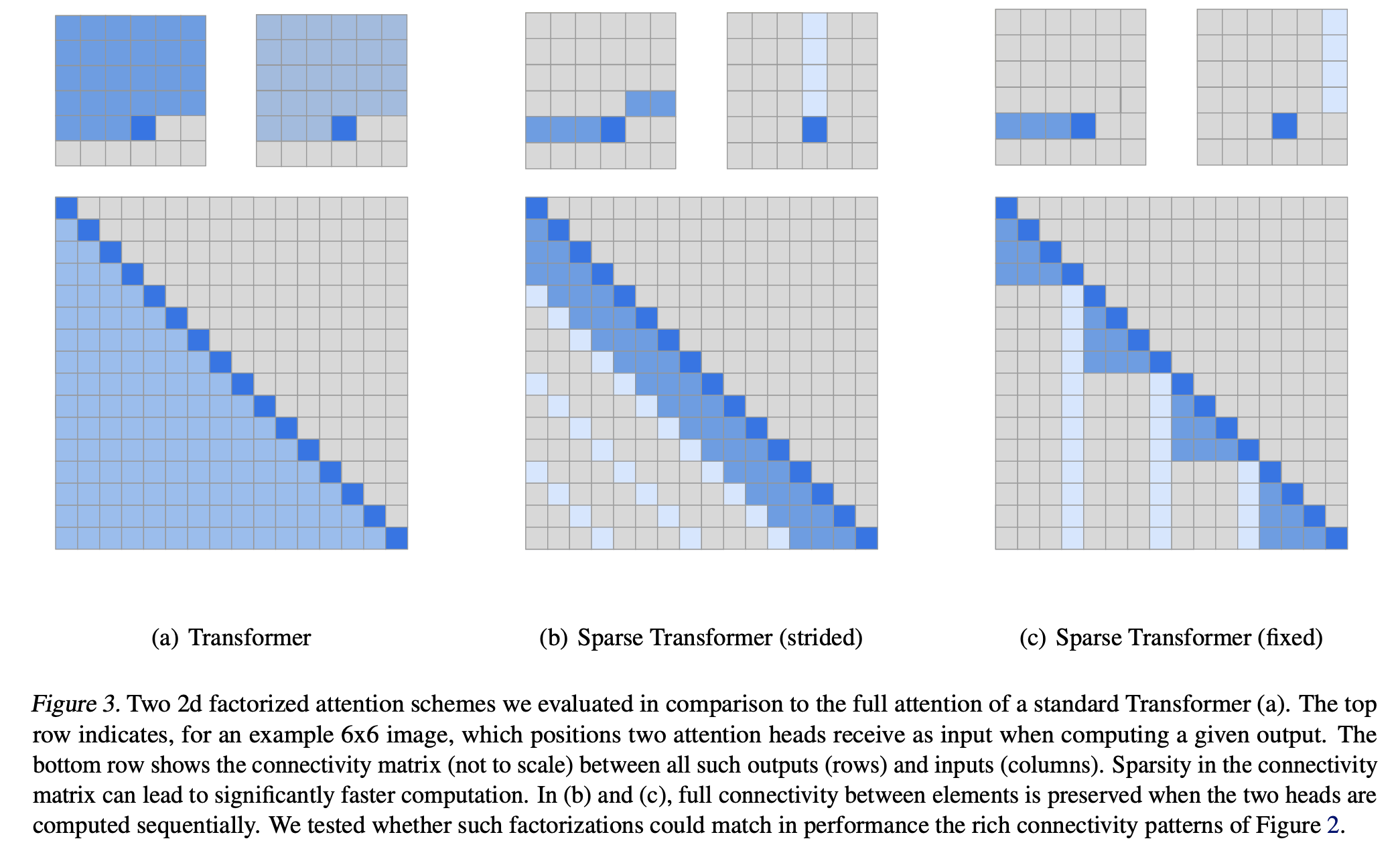
通过组合这些模式,稀疏注意力在保证信息能够有效流动的前提下,使得每个 Query 只需要与 \(O(\sqrt{n})\) 或 \(O(\log n)\) 个 Key 进行计算,从而将总复杂度降低到 \(O(n\sqrt{n})\) 或 \(O(n \log n)\)。
Conclusion⚓︎
| 特性 | 标准自注意力 (Full Attention) | 稀疏注意力 (Sparse Attention) |
|---|---|---|
| 计算/内存复杂度 | \(O(n^2 d_k)\) / \(O(n^2)\) | 通常为 \(O(n \log n)\) |
| 核心特性 | 全局感受野:每个 token 都能直接与序列中任何其他 token 交互。信息流动最充分,表达能力最强。 | 近似全局感受野:通过固定的稀疏模式(如局部+步进)来近似全局连接。是一种权衡效率和性能的方案。 |
| 操作方法 | 计算一个完整的 \(n \times n\) 注意力矩阵,所有 \(Q_i\) 和 \(K_j\) 都进行点积。 | 只计算预定义稀疏模式下的注意力分数。例如,对于 \(Q_i\),只计算它与部分 \(K_j\) 的点积。在实现上,通常通过索引和分块矩阵乘法来高效完成。 |
| 计算流程 | 1. \(S = QK^T\) 2. \(P = \text{softmax}(S / \sqrt{d_k})\) 3. \(O = PV\) |
1. 根据稀疏模式 \(M\) 确定要计算的索引对 \((i,j)\)。 2. 只计算这些索引对的 \(S_{ij} = Q_i K_j^T\)。 3. 在这些计算出的分数上进行 Softmax。 4. 计算输出。 |
| 优点 | 效果最好,能捕捉任意位置的依赖关系。 | 计算和内存效率极高,能够处理非常长的序列。 |
| 缺点 | 复杂度是序列长度的平方,长序列下不可行。 | 1. 是一种近似,可能会丢失部分信息。 2. 稀疏模式是预先固定的,不具备数据驱动的适应性,可能不是最优模式。 |
在计算过程中,与多头、Casual Mask 完美兼容。实际上是把 Mask 的内容变成了原先的下三角阵和一个新的、预定义的Mask矩阵取交集,得到实际参与计算的元素,剩下的全部为 0 了。