CNN 卷积神经网络⚓︎
约 2913 个字 3 张图片 预计阅读时间 10 分钟 总阅读量 次
第一种理解方式⚓︎
我们的任务是图像识别。辨别图像到底属于哪一个物品。也就是输出是一个大小为类别数的向量。 表示为这个物品的概率 (cross entropy)。
对于电脑而言,一张图片可以视为一个3维的 Tensor: \(100 \times 100\) ,有 RGB三个通道 (Channel),也就是说一个图片有 \(100 \times 100 \times 3\) 个pixel,如果我们把这每一个pixel拉直,(因为network的输入必须要变成一个向量),输入全连接层进行训练,输出结果——
这是十分没有必要的。首先,学习一个pixel的属性意义不大(Do we really need "fully connected" in image processing?),其次,pixel数太多,难以训练;更重要的是我们需要考虑图片本身的特性。
Observation 1⚓︎
- Identify some critical patterns
-
比如我们为了识别鸟,可能需要识别鸟嘴、鸟头、鸟的羽毛等,Neuron的作用就是识别这些特征。
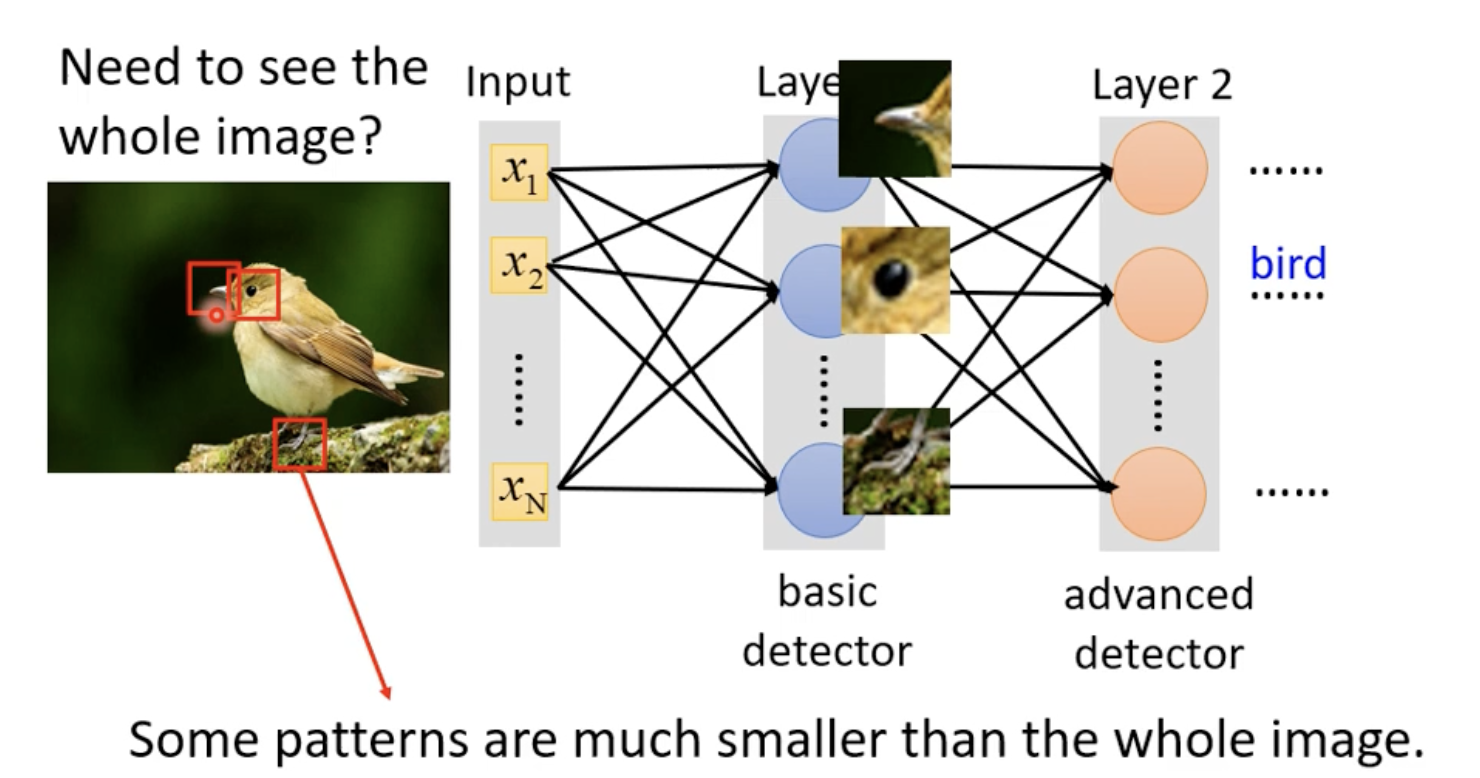
而为了识别这些特征,我们只需要看一小部分输入就可以了,而不需总是看整张图片。
此时我们定义==Receptive Field==,比如一个针对所有Channel建立 \(3 \times 3\) 的小范围,在彩色图片中,也就是 \(3 \times 3 \times 3\) 后拉直的向量,就可以了,这也就是Neuron去“守备”的范围,它的任务就是去识别这小范围内的特征,就好了。
备注: Field 之间是可以重叠的、也可以同个Field有多个Neuron来识别特征;Field甚至也可以有大有小;甚至某个Field只考虑特定的Channel,总之十分灵活;
同时,对于一个 \(3 \times 3 \times 3\) 的 Receptive Field,你肯定希望尽可能多地用 Neuron 去观察它的特征,所以对于每个Field,我们都用多个Neuron去识别模式,比如128个,比如64个,等等。
- Stride
- 我们不希望一个图只有一个Receptive Field,而是需要不断移动这个Field,让Neuron去学习不同区域的特征,所以我们需要移动Receptive Field,这个移动的大小就是
Stride。这个是自己决定的参数,但是一般不会太大。因为我们一般希望这个 Field 是有重叠的。 - Padding
- 随着 Stride ,可能某个 Field 超过了图片边缘,此时就在边缘补 0 / 补均值等等做法。
Observation 2⚓︎
- The same pattern appear in different regions.
-
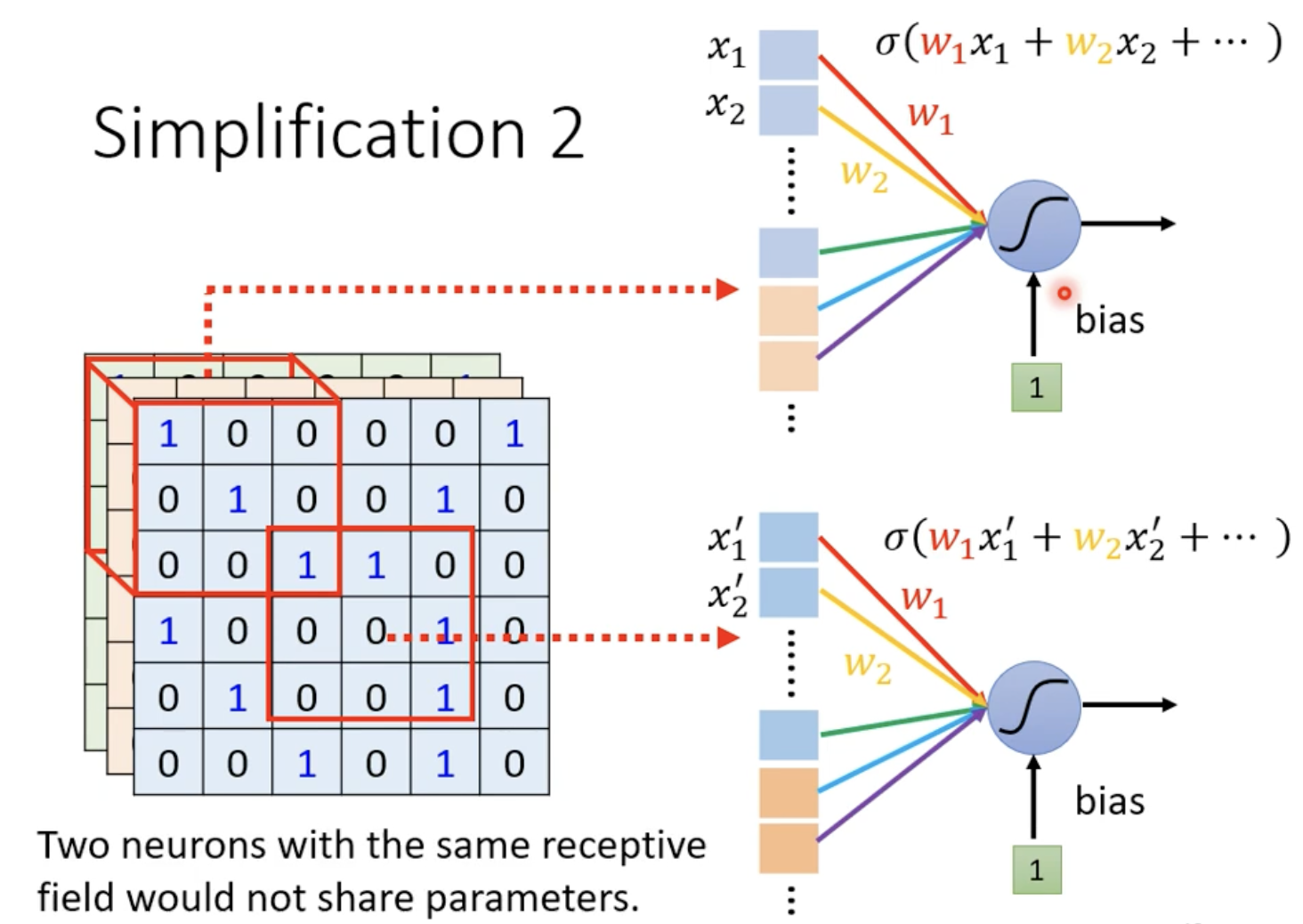
比如,一个鸟嘴可能出现在图片中间、下边、上边 ... 也就是说,对于不同 Receptive Field 的一些Neuron,它们做的事情可能都是一样的(去捕捉的特征就是一样的),只是其 Field 位置不同而已。我们可以省去一些额外的Neuron,而是说,不同位置 Receptive Field 的 Neuron,是共享参数的。 (Parameter sharing)事实上,这个有相同参数的 Neuron 就是一个 Filter .
假如每个Receptive Field有64个 Neuron,那么这 64个 Neuron 的参数是共享的。
Convolutional Layer = Parameter Sharing + Receptive Field
虽然可能带来更大的Bias,但是能在特定任务上做好,比MLP要靠谱很多(表现普通)。
第二种理解方式⚓︎
基于 Filter 的介绍。我们有一些 \(3 \times 3 \times Channel\) 的 filter,这些 filter 的参数是要调的。
我们用每个 Filter,按照 Stride 进行移动,覆盖整个图片,获得一个新的图像,依次类推。你可以认为,每个 Filter 都是具有特定功能的 Detector,比如边缘检测、角点检测等,每个 Filter 都会给我们一些数字,这也就是识别出来的图片的特征情况。一个 Filter 走完整个图,得到的就是一个 Feature Map。也就是一张新的图。但是这个 Map 的 Channel 不再是 RGB了,而是 Filter 的数量。比如我们有 64 个 Filter,那么新的图的 Channel 就是 64。
Filter 这么小,不会随着卷积层深入,能看到的空间越来越小吗?
不是的。正是由于卷积的存在,每个 \(3 \times 3\) 的卷积层都能包含前面更多层操作中汇集的信息,因此,即使 Filter 的尺寸不变,它所覆盖的特征空间实际上是逐渐增大的。这使得深层的卷积层能够捕捉到更大范围内的特征。
而 Filter 是一个一个扫过整张图的过程,就是 “卷积” (Convolution);一个 Filter 扫过整个图,其参数是不变的,也就对应了第一种理解方式中,每个 Receptive Field 的 Neuron,共享参数的过程。
Observation 3⚓︎
- Subsampling the pixels will not change the object
-
我们可以用 Pooling 来实现。Pooling 本身没有参数,没有需要 Learning的东西,只是一种类似激活函数的东西。
MaxPooling: 取一个区域内的最大值,也就是一组里选一个代表。
AveragePooling: 取一个区域内的平均值 ...
类似于 Filter 的移动 、 Receptive Field 的选取,Pooling 的移动也有 Stride,如果发现池化没法完整覆盖所有内容,有一部分多出来了,那么直接把没办法池化的部分删掉就行了。反正下一层还会Padding的。
AlphaGo with CNN⚓︎
首先,下围棋可以视为一个分类的问题:输入是当前的情况,输出就是下一个落子的地方。一个 \(19 \times 19\) 的棋盘,也就是在 \(19 \times 19\) 中分出概率最大的那个类。
CNN的效果被证明比 Fully Connected Network 更好。
我们把当前的棋盘看作是 \(19 \times 19\) 的图片,不过,我们的Channel数更多。我们人为划定了48个不同 Channel,这里每个Channel的数字有不同的含义,比如周围多少子、是否无气等等。总共有48个数字来描述棋盘每个位置的情况。
为什么CNN可以用来下围棋?
- 有些region可能出现在棋盘的不同地方;
- 有些Pattern比整个棋盘盘面要小;
文章的网络介绍
首先,\(19 \times 19 \times 48\) 的原始图片。
首先 Padding 到 \(23 \times 23 \times 48\) ;
然后选择 \(k\) 个 Filter, \(k\) 的数量要调参,最终 选择 192 个;Filter 大小是 \(5 \times 5\), stride = 1;激活函数 ReLU.
第一层输出的结果就是 \(19 \times 19 \times 192\);
从第2层到12层,都是先Zero-Padding 到 \(21 \times 21 \times 192\),再用 \(3 \times 3\) 的 Filter, Stride = 1, 每层都是 192 个 Filter, 激活函数 ReLU;
最后一层用 \(1 \times 1\) 的 Filter,只有1个,但是不同位置设置不同Bias, Stride = 1。得到的结果就是 \(19 \times 19 \times 1\),输入 softmax 进行回归即可。
整个网络没有使用 Pooling 层。
🤔 CNN 没法处理图片旋转、放大、缩小(Scaling, Rotation)的情况。需要数据增强。 (Data Augmentation)
LeNet, 1998⚓︎
手写数字识别。Yann Le Cun. MNIST 数据集。50,000 个训练数据,10,000 个测试数据。
图像大小 \(28 \times 28\), 10 类,一个 Channel;
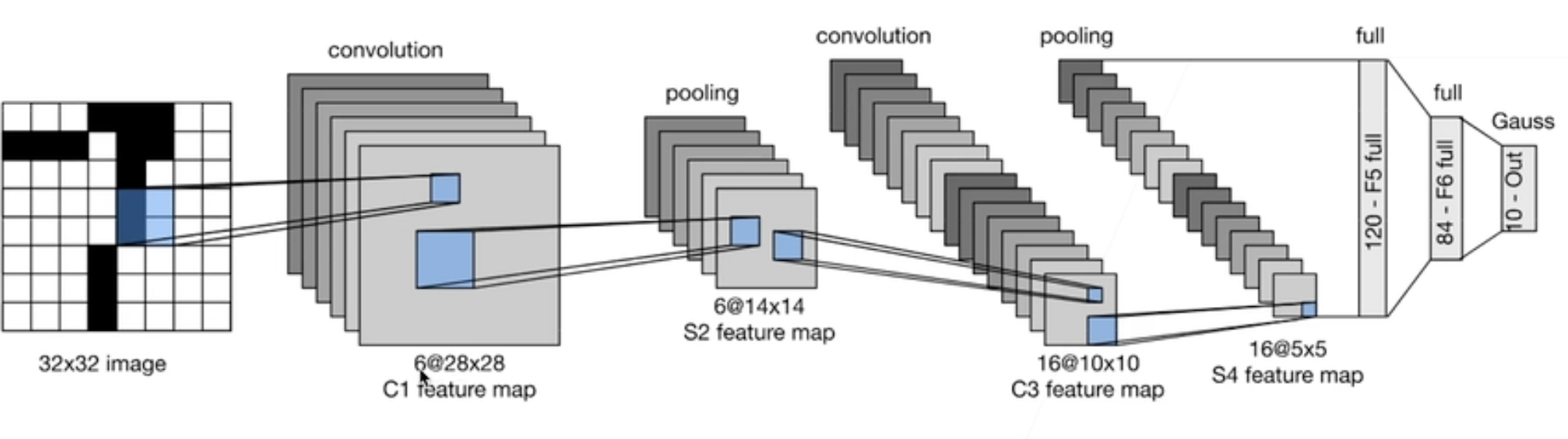
简单来说,两个卷积层,两个Pooling层,最后 SoftMax 回归。
输入是 \(32 \times 32 \times 1\) (After Padding)。
- 第一个卷积层:6 个 Filter,大小 \(5 \times 5\),结果是 \(28 \times 28 \times 6\) 的新图片 (C1)
- 第一个Pooling层:\(2 \times 2\),Stride = 2,用 MeanPooling? 得到 \(14 \times 14 \times 6\)
- 第二个卷积层:16个 filter,大小 \(5 \times 5\),结果是 \(10 \times 10 \times 16\) 的新图片 (C2)
- 第二个Pooling:\(2 \times 2\),Stride = 2,用 MeanPooling? 得到 \(5 \times 5 \times 16\)
- Flatten: \(5 \times 5 \times 16 = 400\)
- 全连接层:400 -> 120 -> 84 -> 10
- SoftMax 回归
AlexNet, 2012⚓︎
2000~2010年的机器学习方法:Kernel Method
- 特征提取、选择核函数来计算相关性、转化凸优化问题;好处是有很好的理论解、显式解、计算证明等。
传统的做法:特征提取 + SVM
AlexNet赢得2012年ImageNet后:通过CNN学习特征;然后进入Softmax回归;
AlexNet:更深更大的 LeNet. 主要改进:
- 隐藏全连接层后加入了Dropout (待补充)
- ReLU激活函数替代Sigmoid,减缓梯度消失;
- MaxPooling
- 数据增强
代表了计算机视觉方法论的转变。
这一部分来自李沐《动手学深度学习》,注意,李宏毅老师讲的 Filter,其实就对应着每一个卷积层用来卷积的通道数,因此下面统一把Filter称为Channel
网络结构与矩阵维度尺寸详解:
- 原始图片
- \(224 \times 224 \times 3\) 的图片。彩色。
- 第一个卷积层 (Conv-1)
- \(11 \times 11\) 的 Channel, 共 96 个,stride = 4. 此时参数量就有 \(11 \times 11 \times 96 \times 3\),因为有 3 个 Channel,并且当前有 96 个 Filter;这一层没有做Padding(所以224只截取断223,所以结果为 \(54 \times 54 \times 96\))
- 第一个池化层 (Pool-1)
- \(3 \times 3\) 的 MaxPooling, Stride = 2,这一层同样没有Padding,所以Stride只截取到53,结果是 \(26 \times 26 \times 96\)
- 第二个卷积层 (Conv-2)
- \(5 \times 5\), 256 个 Channel, Pad 2. Stride 是1,做了Padding,这里可以验证,Padding是要在两端都加,不只是加一端的,相当于加了4,就是 \(30 \times 30 \times 96\),这个图做Stride = 1的 \(5 \times 5\) 卷积,考虑有 256 个 Channel,就是 \(26 \times 26 \times 256\),与试验结果匹配。
- 第二个池化层 (Pool-2)
- \(3 \times 3\) 的 MaxPooling, Stride = 2,相当于是 \(12 \times 12 \times 256\)。同样注意,没有Padding,这里是直接截断多余的部分。所以长度是12)
- 第3 到 5个卷积层 (Conv3-5, 新增的)
-
\(3 \times 3\),Channel = 384,Pad = 1, Stride = 1,考虑到 Padding后 是 \(14 \times 14 \times 256\),此时处理后的结果就是 \(12\times 12 \times 384\)。
注意,Conv-3是把Conv-2的Channel从256拓展到384了,在Conv-4的时候依然是384Channel,但是从Conv-5还要把这个再恢复到256. 所以,第五层输出的依然是 \(12 \times 12 \times 256\).
- 第三个池化层 (Pool-3)
- \(3 \times 3\) MaxPooling, Stride = 2;同样注意,没有Padding,这里是直接截断到 11,多余的部分舍去。所以长度是5)结果是 \(5 \times 5 \times 256\)。这个拉平之后,就是 6400,对应进入MLP的维度。
注意,每一个Conv Layer 都由 ReLU来激活,上面没有写出来。 池化层不需要激活函数。
同时,在MLP中融入dropout。
参数的计算:尺寸 \(\times\) 输入的通道 (Channel,也就是LHY老师的“Filter”) 数 \(\times\) 前的一层的Channel数
VGG, 2013⚓︎
使用块的网络。针对 AlexNet结构不够清晰解决的。“怎么让神经网络更好地变深、变大”。
选项
更多的全连接层:不一定好,因为占用的空间太大;
更多的卷积层?“怎么堆叠?”
VGG的思想:将卷积层堆积成“块”,然后把卷积块不断摞上去。 可以视为AlexNet思路的拓展。比如AlexNet中连续三个卷积层,把它垒起来,三个 Pad = 1,\(3 \times 3, 384\) 个Channel 的卷积层集中在一起。这里需要决定的超参数就是层数 (叠几个),还有通道数,依次决定pading的大小。
尝试用 \(3 \times 3\) 和 \(5 \times 5\) 分别来做这个块的堆叠。比较性能和效果。 发现深+窄的效果更好。 堆得更深效果更好!
VGG 同样修改了池化层的大小。
总之,VGG通过不同次数的重复得到不同的架构 。VGG-16, VGG-19. 最终回到全连接层。更加整洁,更加规则,最终的网络就是 N 块东西串在一起。其核心思路就是使用可重复堆叠的卷积块来构建深度卷积神经网络,不同的卷积块个数和超参数可以获得不同复杂度的变种。