深度学习 | 王树森⚓︎

约 6721 个字 59 张图片预计阅读时间 22 分钟总阅读量次

数据处理基础⚓︎

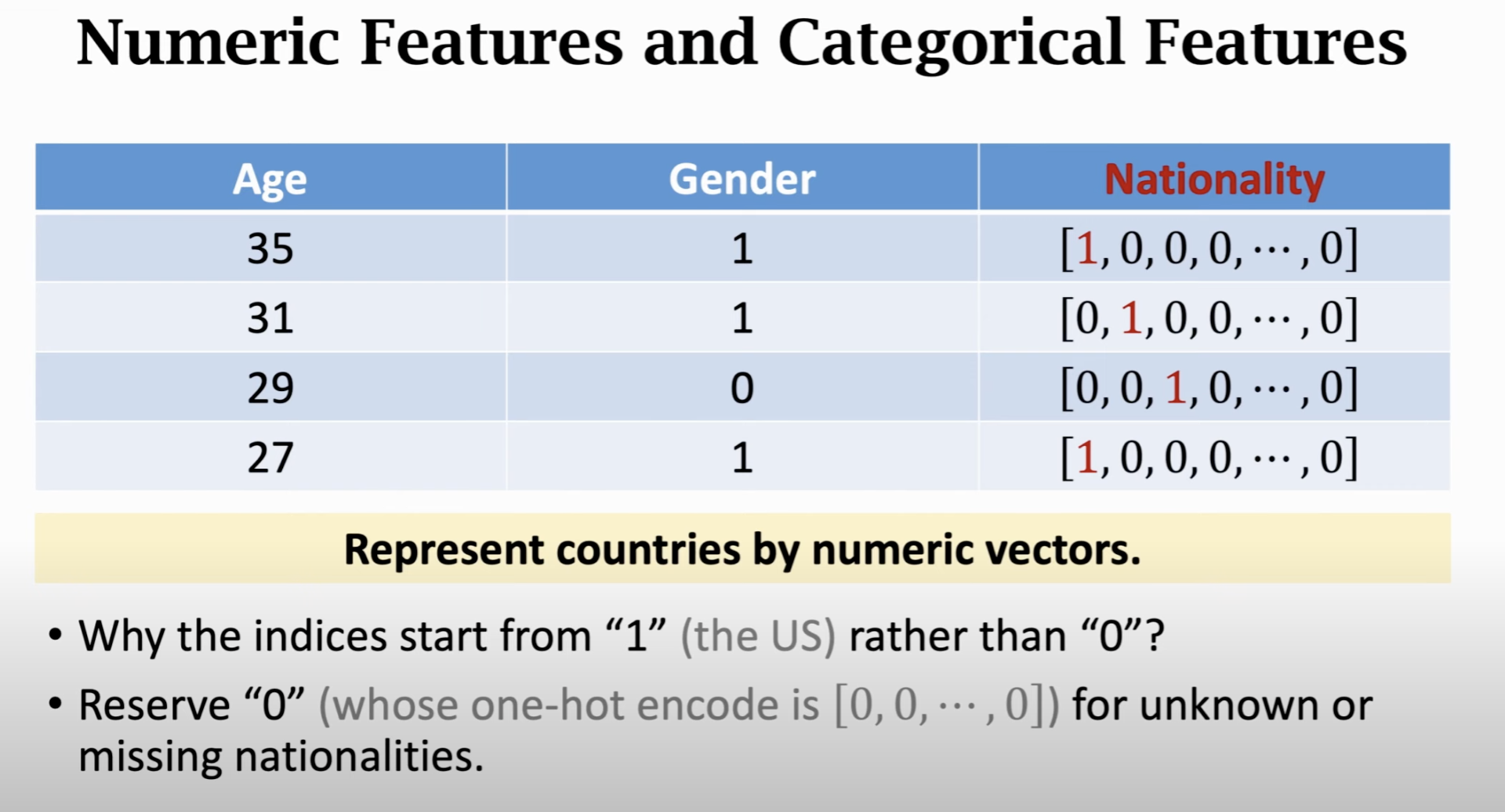
上图展示了几种常见的处理：

数字类型，比如年龄；
二分类，比如性别，用 0/1表示；
Categorical data，比如国籍，这里需要用到 one-hot embedding。比如有197个国家，那么就有一个长 197 维的向量，每个索引对应一个国家。是哪个国家则对应数字为1，其他为0

为什么不用那个国家的数字进行表示呢？

答：这样的话不同国家之间就是可加减的了：1 + 2 = 3，这是不符合情况的。而 One-hot则可以更好地表示: [1,0,0,...,0] + [0,1,....0] = [1,1,0,0,0...,0]

同时，对于没填写这一栏的用户，直接让这个向量每个元素为0即可。

于是，上面的数据可以表示为如下的向量：

对于文本数据，我们首先可以做的就是统计词频，并且按照词频大小从高到低排序，剔除掉频率低的词，仅保留前一部分。这样的好处是：

删除一些无意义的词，比如名字；
删除一些笔误 Typos，比如 prince / prinse；Hamlet, Hemlet

文本处理与 Word Embedding⚓︎

以IMDB文本分类为例：

Tokenization

也就是把句子切分成单词（或者字符）的过程。注意几个细节：

大小写是否转换 (Apple, apple)

停用词 (A, the, of)

对错误拼写的纠正：gooood -> good

Build dictionary

也就是把每个单词映射到一个索引（Index）中。

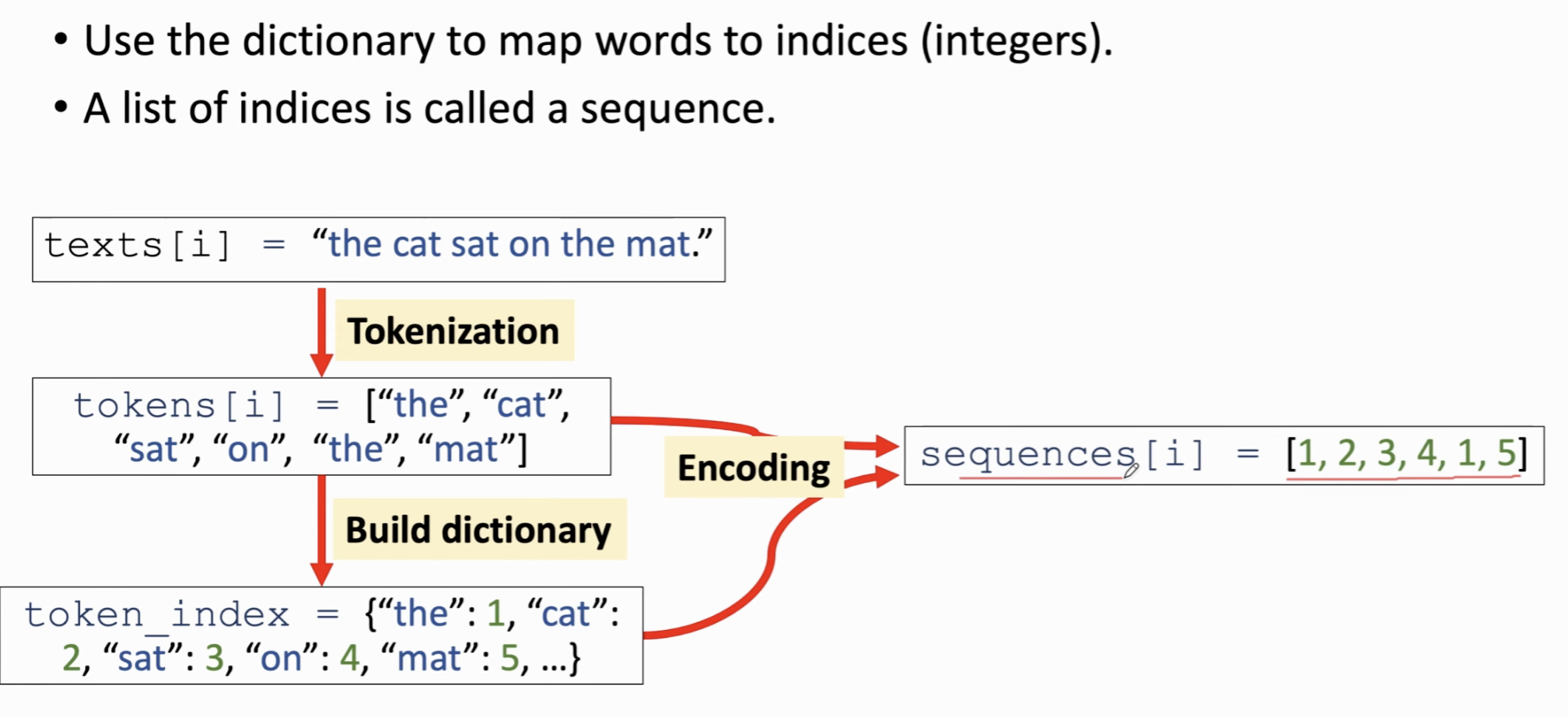
One-hot encoding

对数据里的每一段文本进行encoding，encoding后的向量长度是这段话里的Token数（Tokenization）。此时你会发现每一段文本都不一样长。

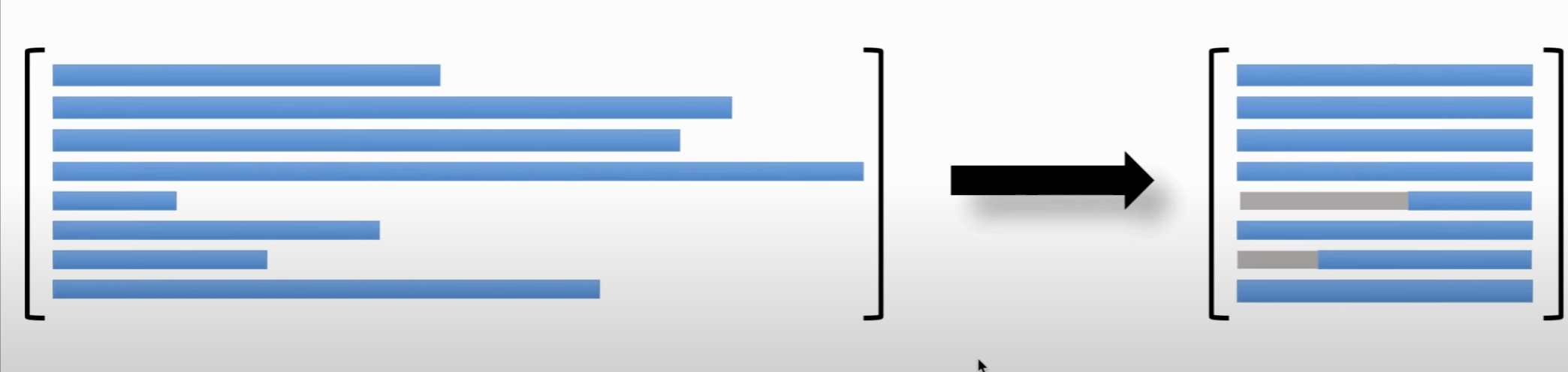
Text Alignment

考虑到每个文本不一样长（Token数不一样），而我们希望把数据存储在矩阵或者向量里面，因此我们希望每一段文本都是一样长的，也就是需要把长的截短（仅保留后 M 个，或者前 M 个 Token），以及把短的变长（zero padding），在前面补上 Null凑成更长的向量。

Word Embedding⚓︎

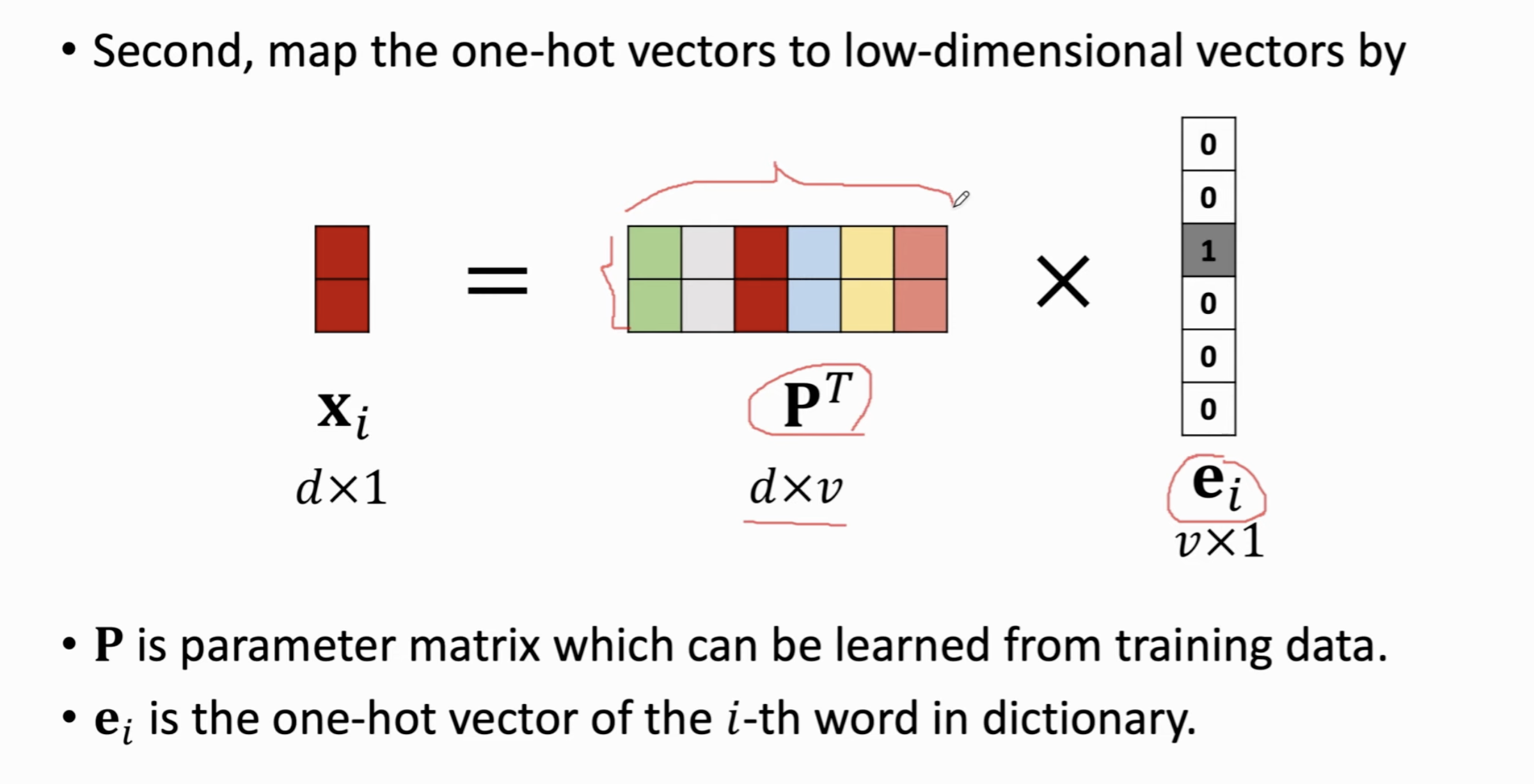
对于文本而言，用One-hot embedding来表示每一个Token太奢侈了，因为字典很长（10K），而句子里又有很多Token。

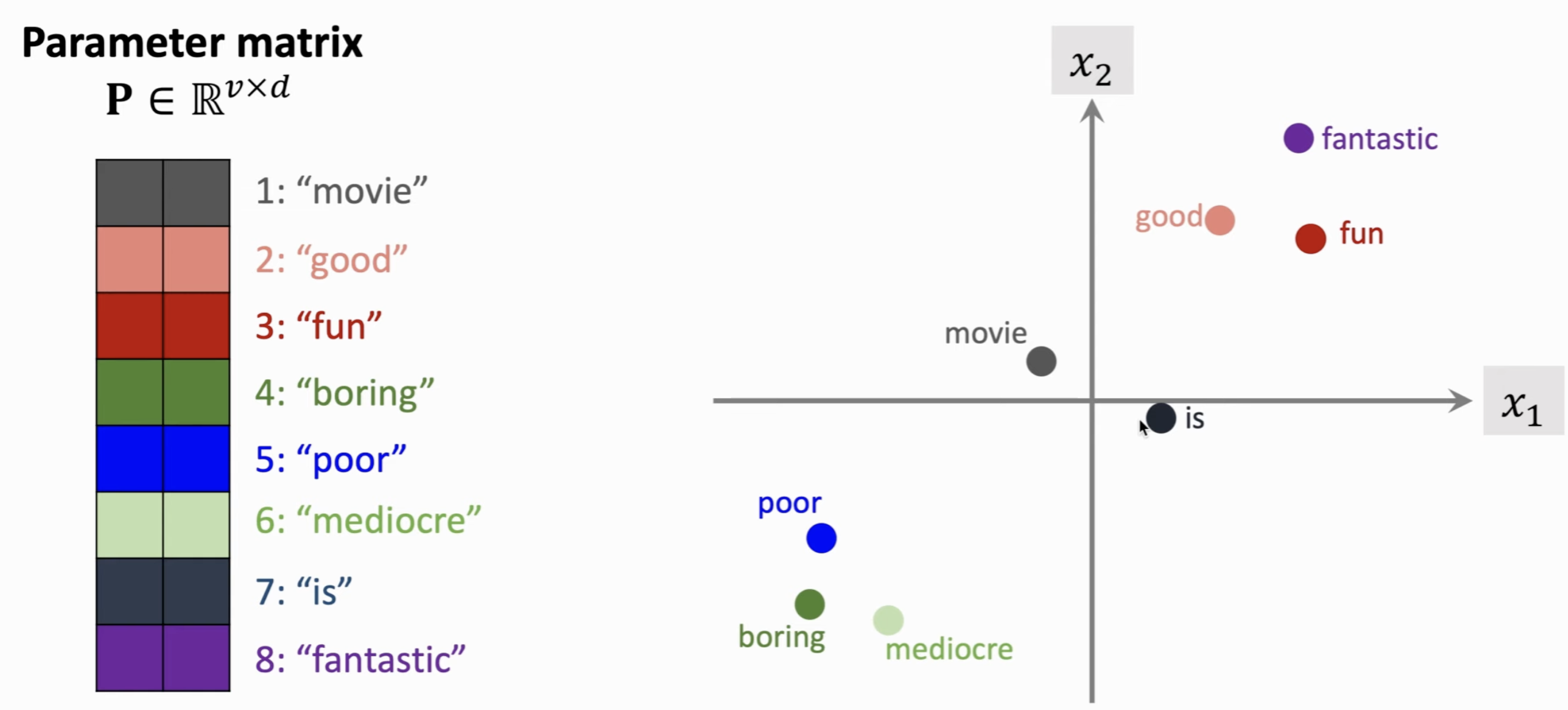
我们如何实现呢？我们可以基于每个Token的One-hot向量，应用一个参数矩阵 \(\mathbf{P}^T\) 和One-hot向量 \(\mathbf{e}_i\) 的乘法，把一个Token映射成一个低维度的向量 \(\mathbf{x}_i\)。这里的 \(d\) 是Token Embedding的维度，需要用户自己指定，\(v\) 是字典里Token的数量。

我们机器学习训练的时候就是在根据训练数据调整这个 \(\mathbf{P}^T\)

可以想象，参数矩阵 \(\mathbf{P}^T\) 的每一列就表示一个Token的感情色彩。

Logistic Regression⚓︎

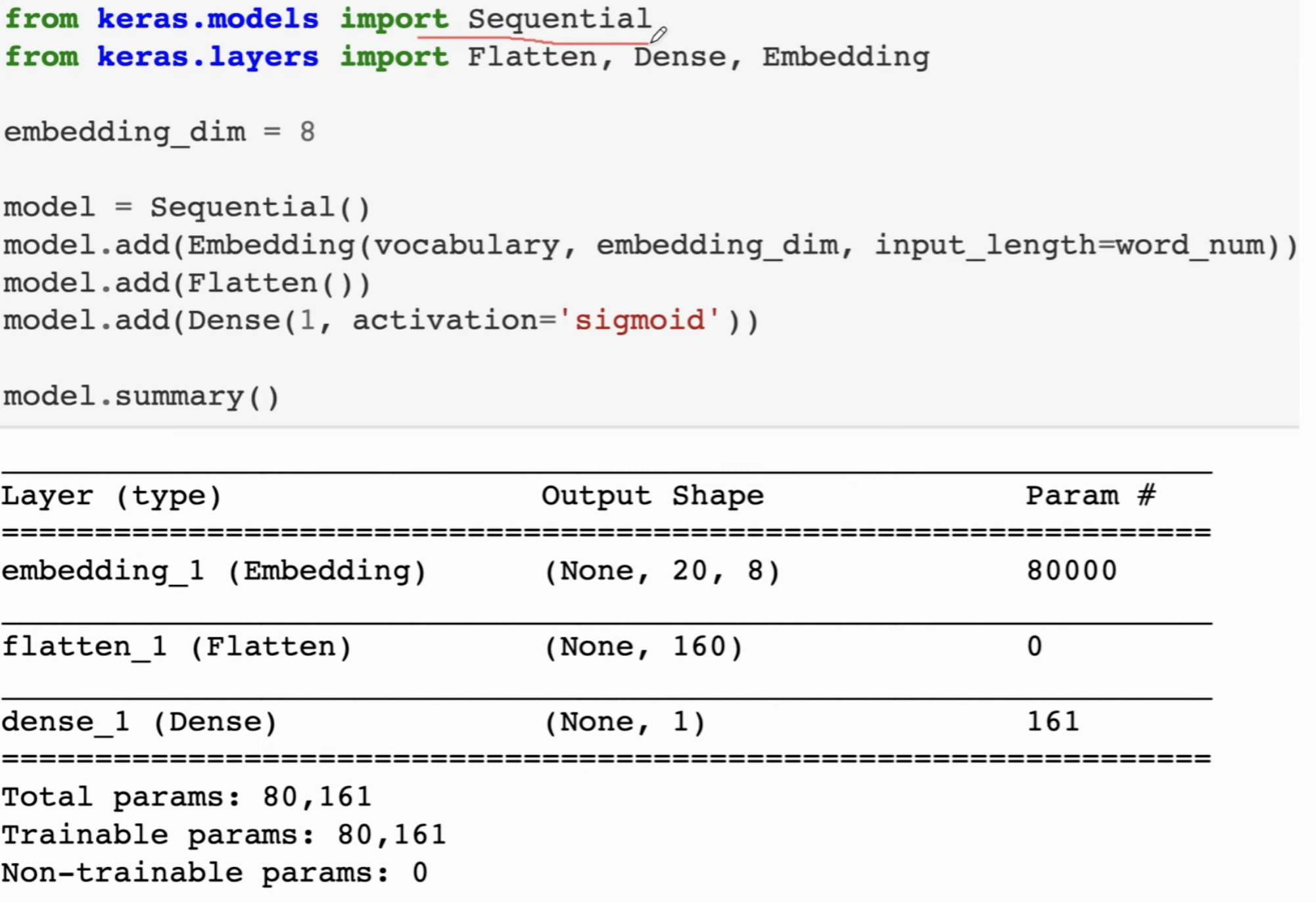
设置词向量的维度是 8 （Cross- Validation确定），同时每一个评论取20个Token。先对它进行Embedding，这样每一个评论就变成了 20 * 8；把它压扁变成 160 的向量；最后一层全连接层，其实就是Logistic Regression，因为我们约束输出在 0~1 之间并且用 sigmoid 函数激活。

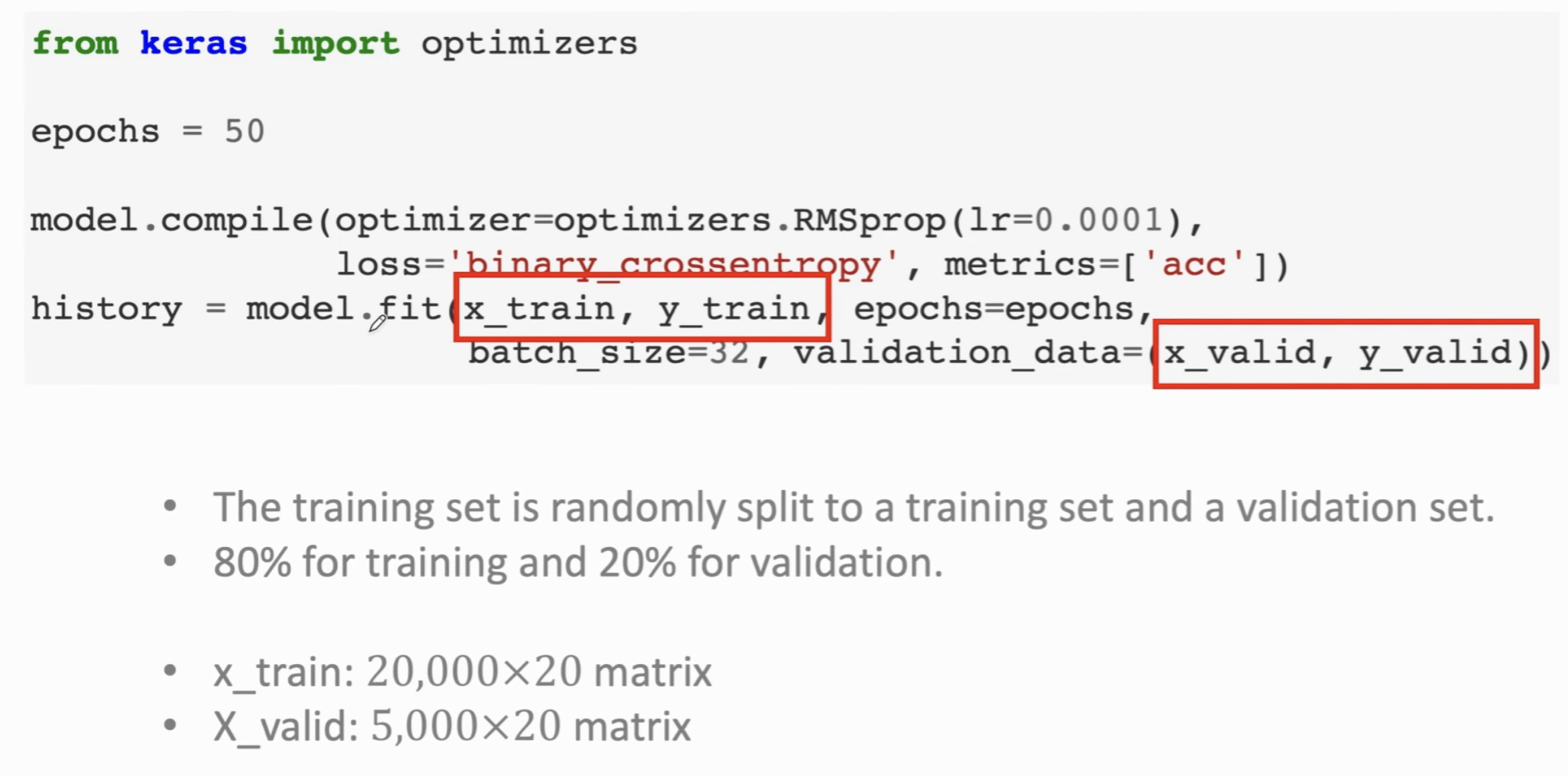
解释一下 Epoch，把所有的训练数据（20000/25000,5000做 Validation）从头到尾扫一遍，就是一个 Epoch。50 Epoch 意思是把训练数据扫50遍；

整个流程如下：

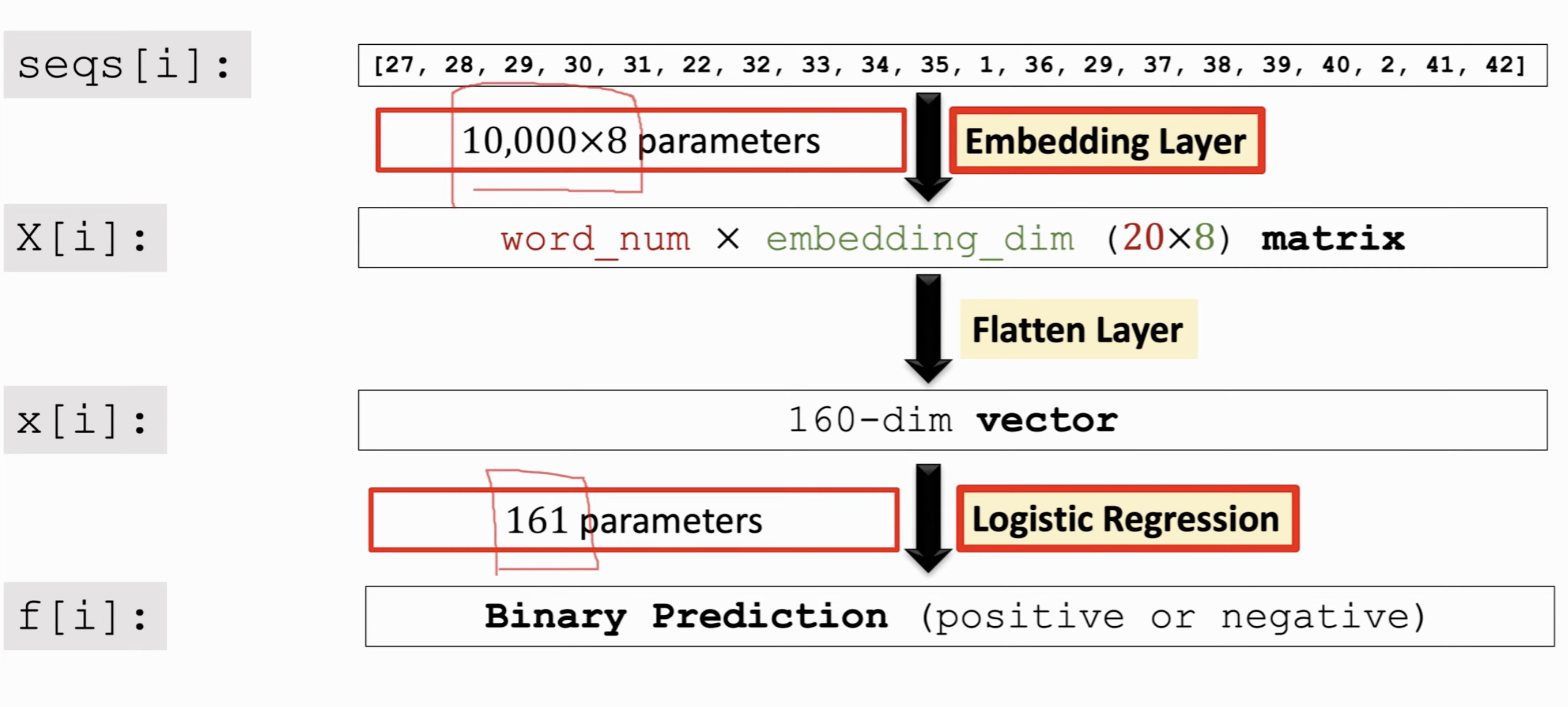
161 Parameter，是因为还有一个偏移量。

RNN⚓︎

与全连接层、CNN不同在于，序列数据不是 One to One的，而是 Many to One/Many的，（比如，CNN的常见任务是给一张图，输出一个结果，分类，概率，这是One-to-One），但是文本/语音翻译/分类，是需要通过句子的若干部分输出一个/一些回复，其长短不一。

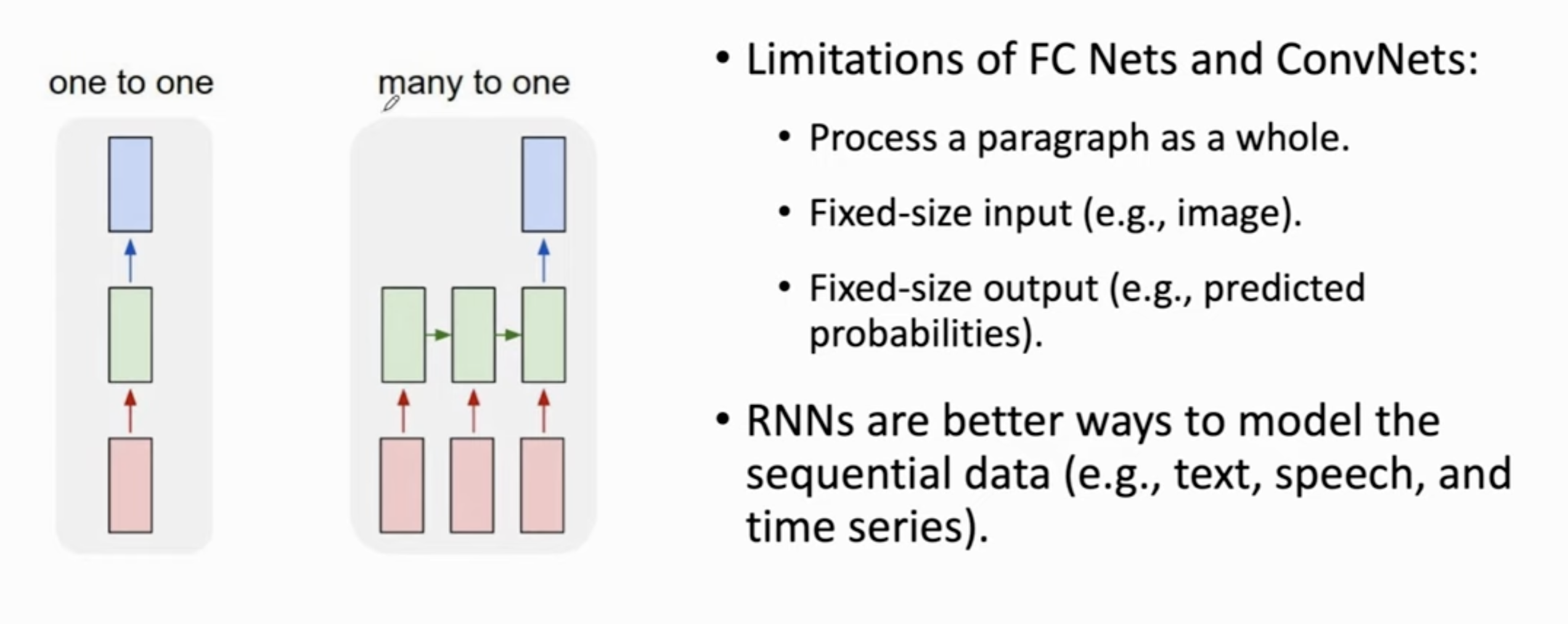
以下是经典的 RNN 的示意图。

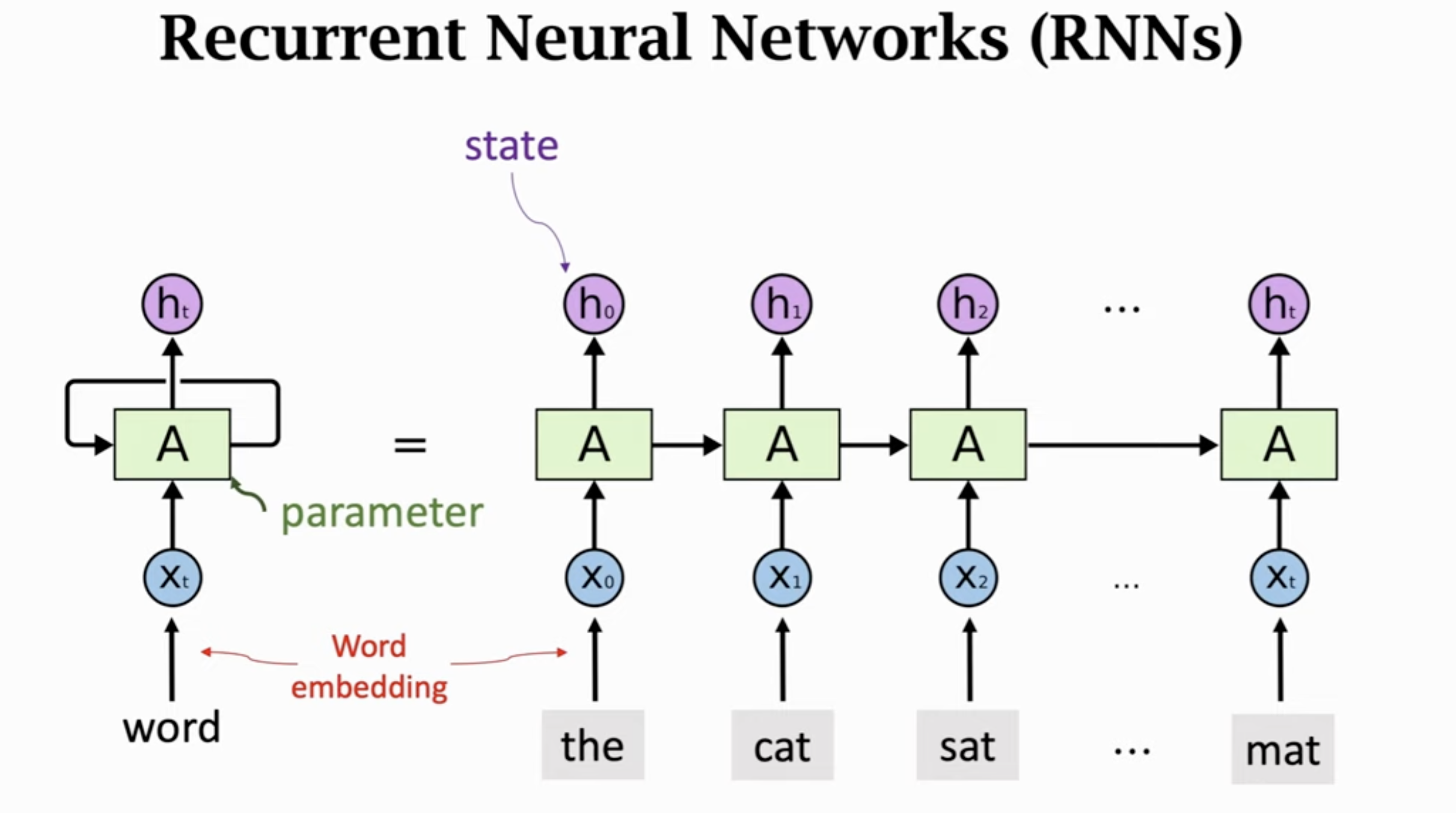
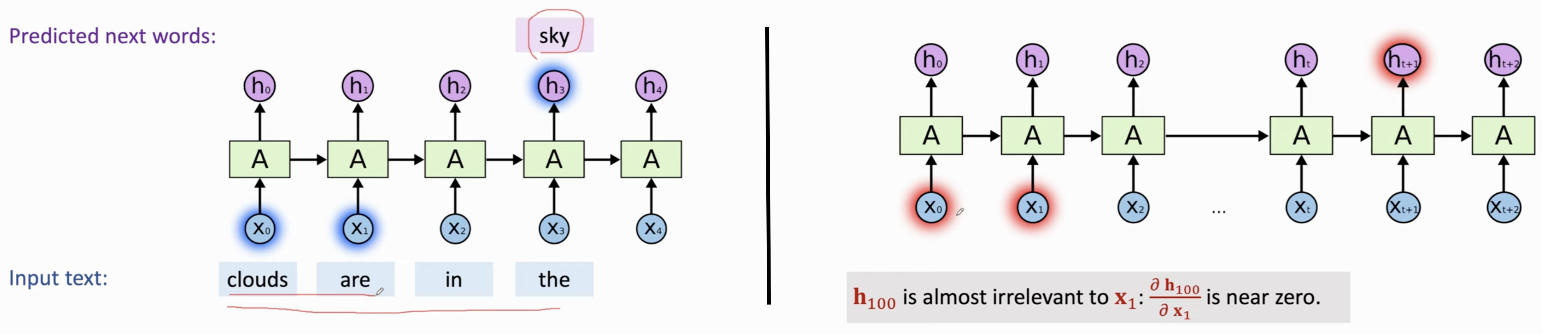
按照句子的阅读顺序，在 The 的时候，对这个词进行Word Embedding，然后产生状态向量 \(h_0\)，到下一个词 cat，对这个词进行Word Embedding，更新状态向量 \(h_1\)，这个向量就包含了 the 和 cat 的信息，以此类推。最后一个状态 \(h_t\) 就是整句话的信息都包含在内的一个向量（它积累了信息！）。

注意在这个过程中，参数矩阵 \(A\) 是一直没有变化的。

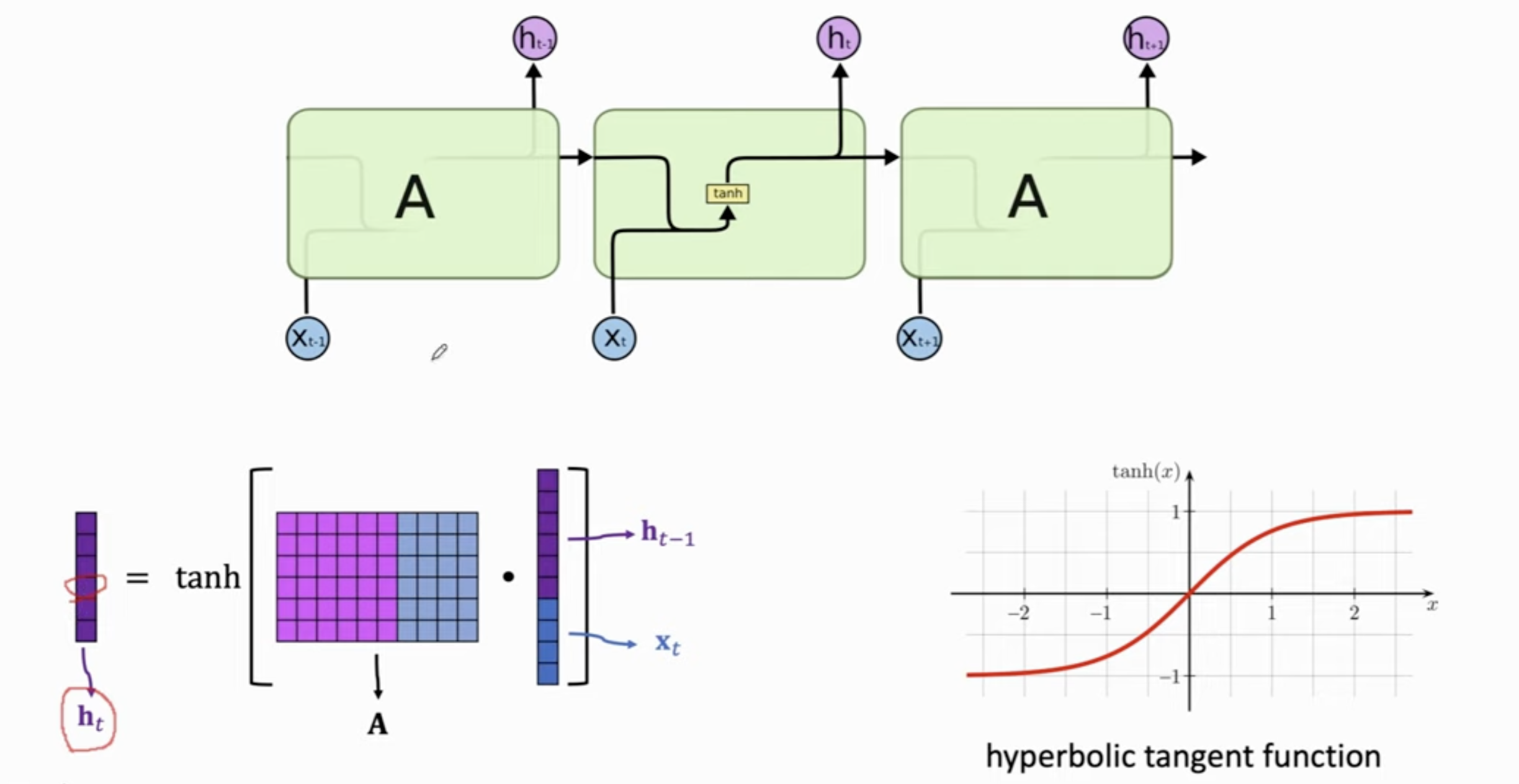
具体而言，我们如何通过 \(h_{t -1}\) （前一个Token的状态向量）和 \(x_{t}\) （Token做embedding后的向量）计算出 \(h_t\) 呢？

做法就是将 \(h_{t -1}\) 和 \(x_{t}\) concat成一个长的向量，和参数矩阵相乘，得到的结果还是一个向量。

对这个向量的每一个元素做 \(\tanh\) 激活函数，将数值压缩到 -1 和 +1 之间。

为什么需要 \(\tanh\)，可否去掉？会发生什么？

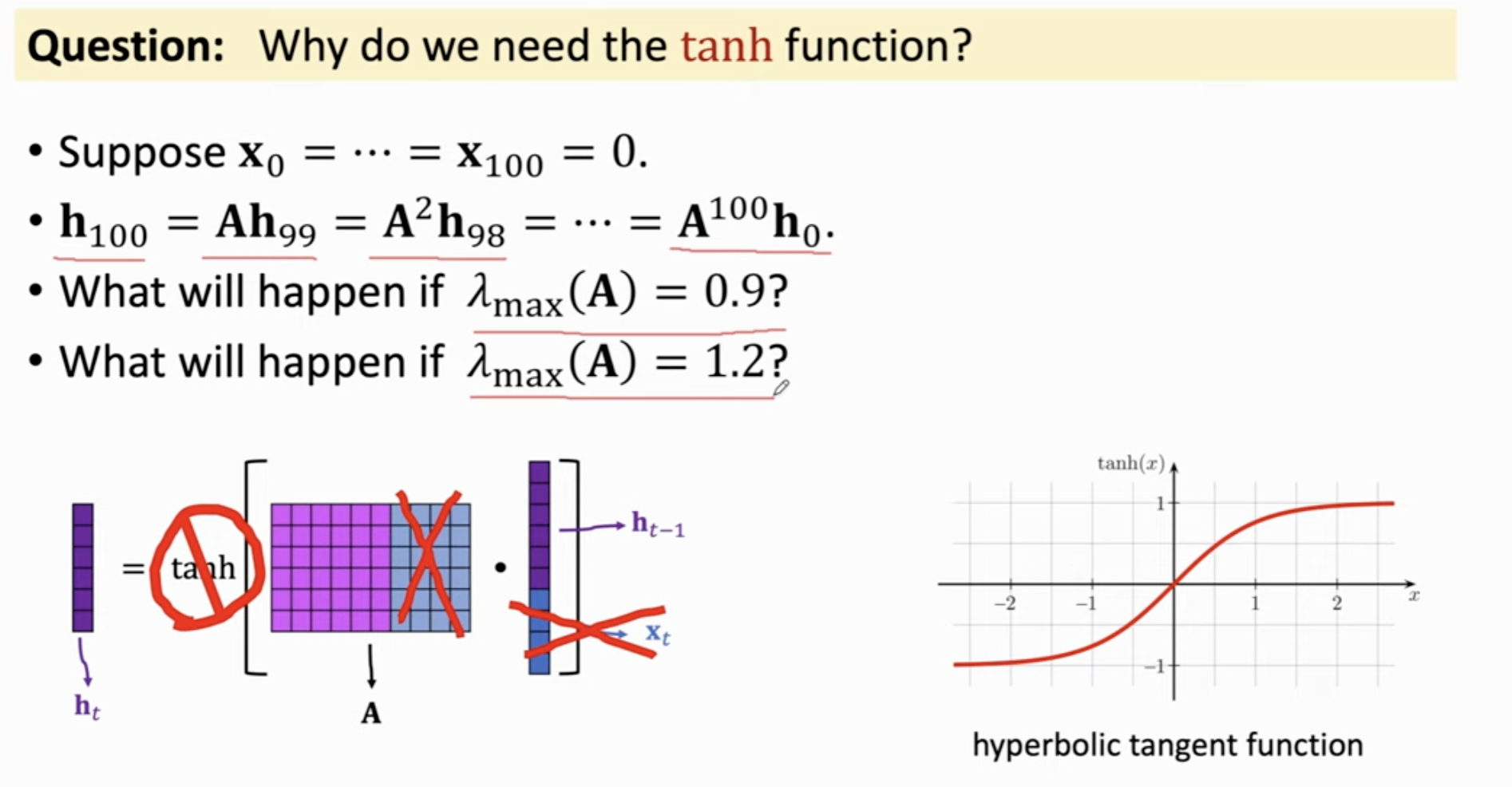
假如某个embedding为0，此时\(h_100\)会退化到 \(A^{100}h_0\)，如果 A 的特征值 0.9，那么此时这个向量会非常小；如果特征值稍大一点，那么这个乘积会超级大。通过 \(\tanh\)，我们成功把每次矩阵乘法得到的结果压缩在一个合理的区间内。

参数量的计算｜结果的计算⚓︎

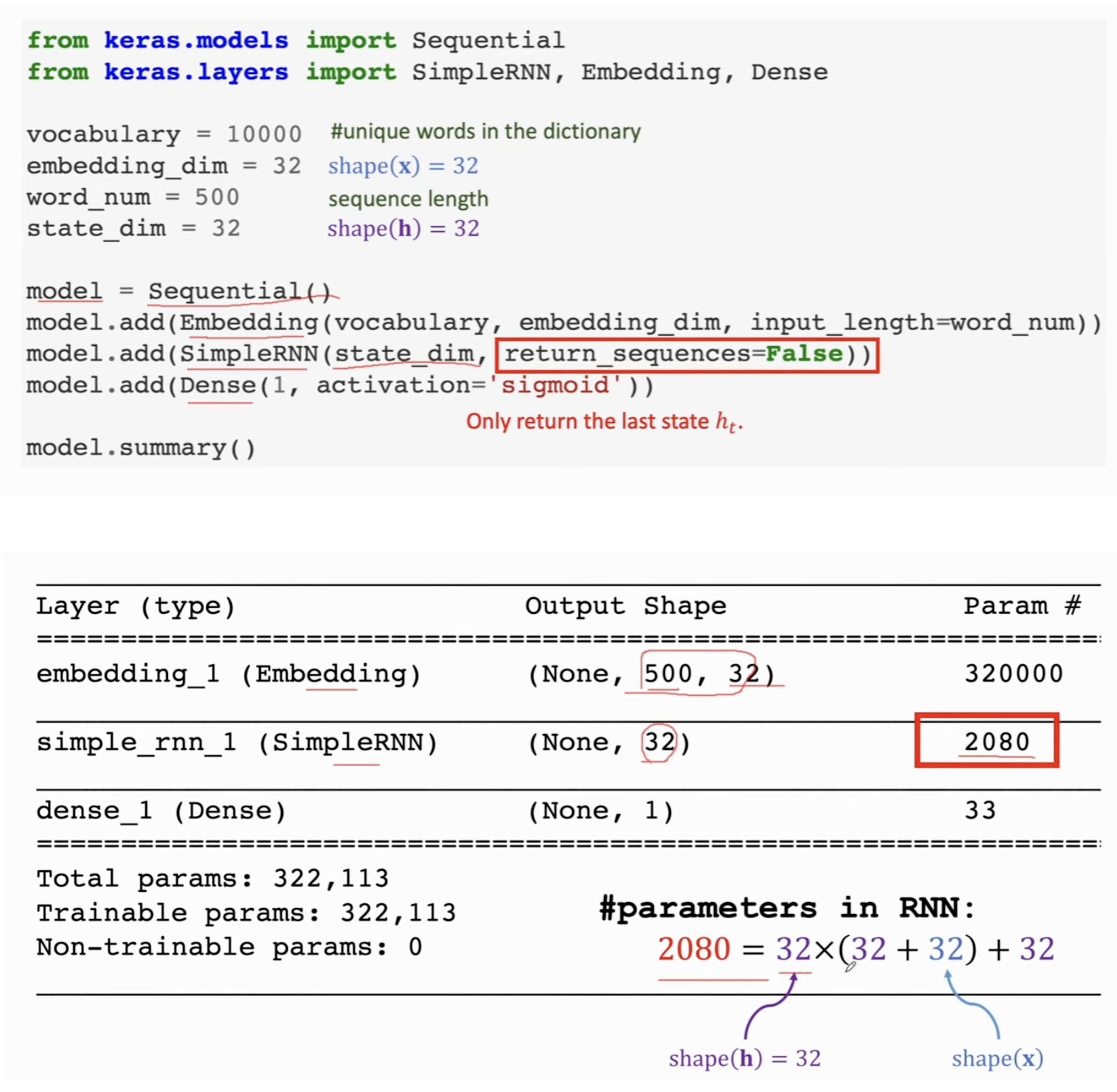
参考上图，\(\mathbf{A}\) 的行数和状态向量的维度是一样的，而列数等于状态向量和embedding向量concat后的向量长度。因此\(\mathbf{A}\) 参数量 = shape (h) \(\times\) [shape(h) + shape(x)]

由于状态向量总是积累了其在之前文本的所有信息，因此我们只需要用最后一个Token的状态向量（相当于一个特征），把它丢入分类器，做sigmoid，也就会输出一个分类的结果了。

比如下图我们就以文本长度500，embedding=32进行对齐，状态向量维度32，每次仅保留最后一个Token的状态向量。此时需要2080个参数（考虑到最后的全连接层）。

存在的问题⚓︎

非常擅长短期预测 (Short Term Prediction)，但是对于很多Token前的，遗忘很严重。如果步长很长，那么它很容易遗忘先前的信息。

LSTM⚓︎

类似RNN的一种循环神经网络，但是要复杂很多。RNN只有一个参数矩阵，LSTM有四个。

传输带 （Conveyer Belt），过去的信息直接通过传输带传送到下一个时刻不会发生太大变化，LSTM就是借助传输带，避免梯度消失的问题。
遗忘门

\(f_t\) 是上一个状态 \(h_{t -1}\) 和当前输入 \(x_t\) 的函数，具体而言是用 \(W_f\) 和二者的concat做矩阵乘法得到一个向量，对这个向量做sigmoid激活函数，得到 \(f_t\)。其大小和状态向量\(h_{t-1}\) 是相同的，每一个元素都在 (0, 1) 之间。

这里有一个遗忘门的参数矩阵 \(W_f\)，需要通过反向传播学习。

输入门

需要计算一个输入向量 \(i_t\)，方式和遗忘门相同（用一个参数矩阵和concat后的状态向量+输入做矩阵乘法，然后sigmoid），这里需要学习一个参数矩阵 \(W_i\)。

New Value 门除了这个输入向量外还要计算一个New Value向量 \(\tilde{C}_t\)，这里做法同上，区别在于激活函数是 \(\tanh\)，这里的向量每个元素都在 \((-1, 1)\) 之间。注意了，这里我们还需要学习一个参数矩阵 \(W_c\)。

现在，我们有了前面几个环节的结果，是时候利用传送带了。如下图所示。我们利用遗忘门输出 \(f_t\)，前一个状态向量 \(C_{t-1}\)，输入门 \(i_t\) 以及Value向量 \(\tilde{C}_t\)，更新传送带上的状态向量 \(C_t\)。由于我们先前保证了 \(C_t\) 和 \(f_t\) 以及 \(i_t\) 的尺寸相同，因此可以做 Element Piecewise Multiplication.

譬如 \(f_t c_{t-1}\) 的结果表示在当前状态选择性地遗忘掉先前状态的东西；\(i_t \tilde{c}_{t}\) 表示向传输带上添加某些新的信息。

输出门

此时我们更新LSTM的输出。此时我们依然是把两部分做concat，然后学习一个参数矩阵 \(W_o\)，经过sigmoid 后输出一个输出向量 \(o_t\)，这个向量的大小，与传送带上涉及的若干向量都是相同的。

这个时候我们需要更新状态向量 \(h_t\)，对于传送带上的信息 \(C_t\)，做 \(\tanh\) 之后与输出向量做Element Piecewise Multiplication即可。这里的 \(h_t\) 既作为下一个状态的状态向量，又可以作为当前的输出结果，因此做2个copy。

综上所述，这里的参数量由4个参数矩阵构成，分别属于：遗忘门、输入门、新值门、输出门。每个参数矩阵的参数规模 shape(h) \(\times\) [shape(h) + shape(x)]，总参数规模 4 \(\times\) shape(h) \(\times\) [shape(h) + shape(x)]

总而言之，LSTM通过一个传送带，让过去信息容易传输到下一时刻，实现了比RNN更好的长期记忆。

提升RNN的若干技巧⚓︎

多层RNN (Stacked RNN)⚓︎

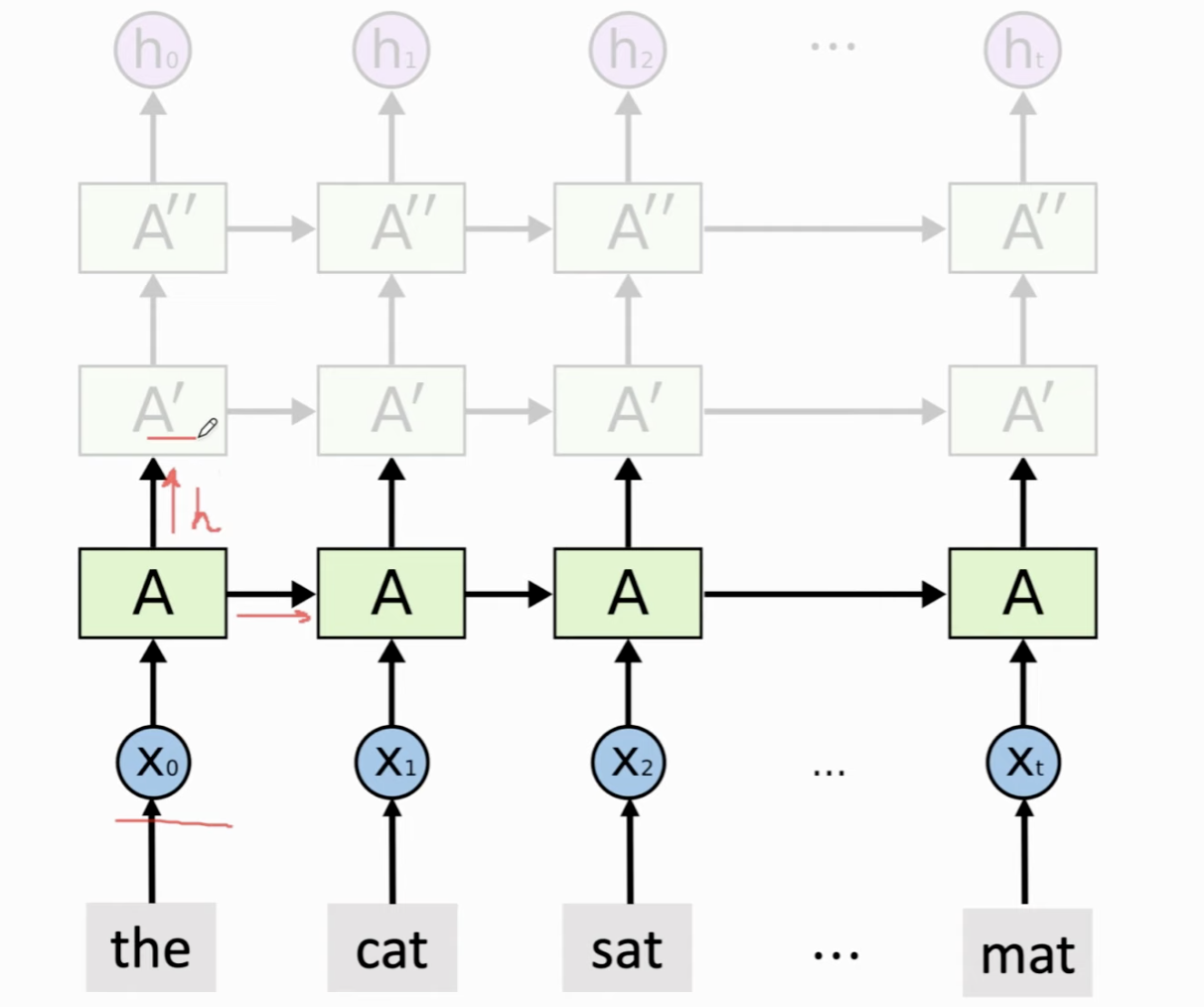
类似于深度卷积神经网络。原先的RNN，每一个输入的状态向量都直接作为输出以及下一个状态向量，而我们可以在此基础上再堆叠一个 RNN，这个RNN的输入不再是embedding了，而是前一个RNN的状态向量，这个第二层RNN有自己的模型参数，会更新和输出自己的状态向量 \(h\)，而这个状态向量又会作为第三层RNN的输入，以此类推，越来越深。

最上层RNN的状态向量就是最终的输出了，可以用最后一个状态 \(h_t\) 可以视为从最底层的数据提取的特征。

我们可以直接上堆叠一个LSTM，效果是类似的：

实现如下，注意保存 return_sequences。最后将最后一层的状态向量丢入MLP中输出分类结果。

计算参数量的时候，4 * 65 * 32，因为concat后有一个偏移项的参数也不能遗忘。

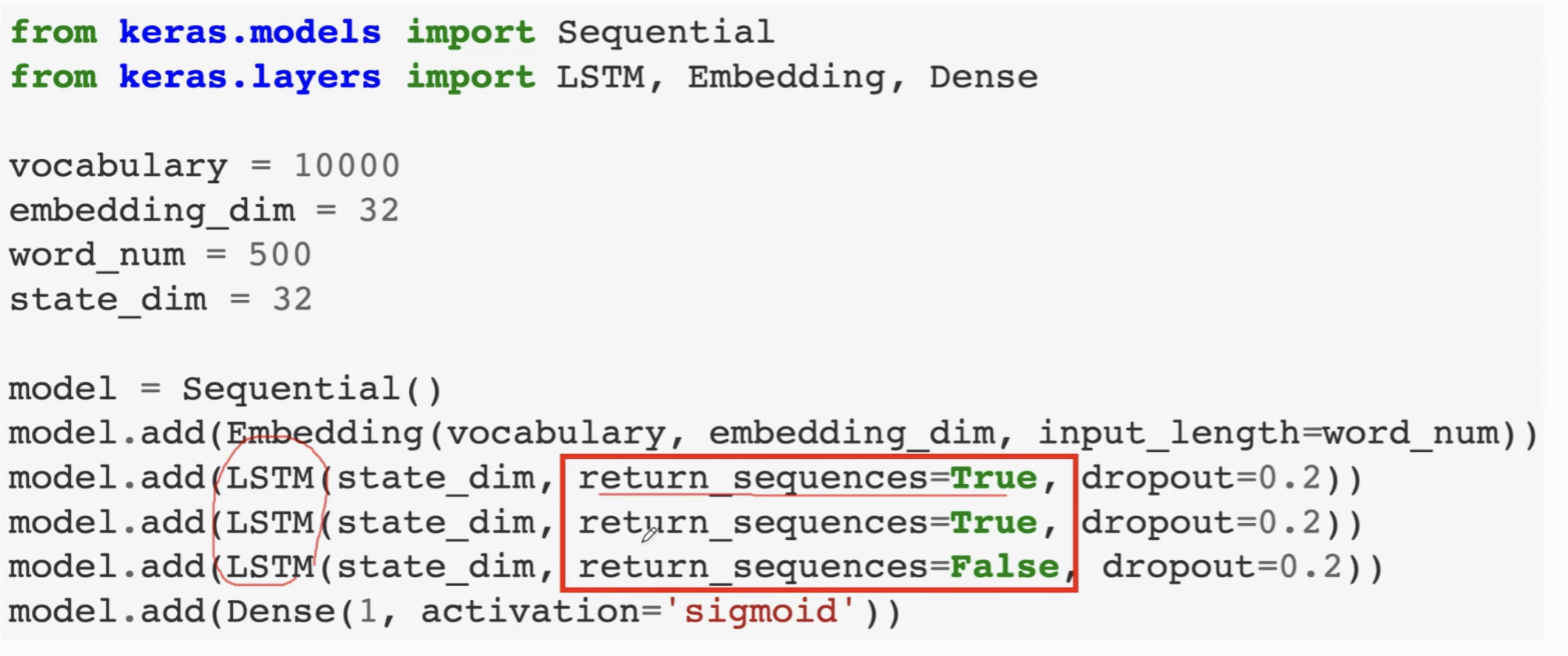
参数统计如下。注意embedding层的参数量很大（缺少足够的数据把这部分训练好，很容易overfitting），同时，在第一和第二层，我们输出了500（文本长度）个状态向量（大小为32），也就是每个状态向量都被我们输出了。

注意，上图中可以让4个阶段的向量尺寸有所不同，不一定都是相同的。

双向 RNN (Bidirectional RNN)⚓︎

人类有阅读习惯从左向右从上倒下，但是从右往左进行阅读同样可以帮助我们对文本进行分类。对RNN而言，阅读顺序变化并么有太大区别。训练一个从后往前的RNN同样会有很好效果。

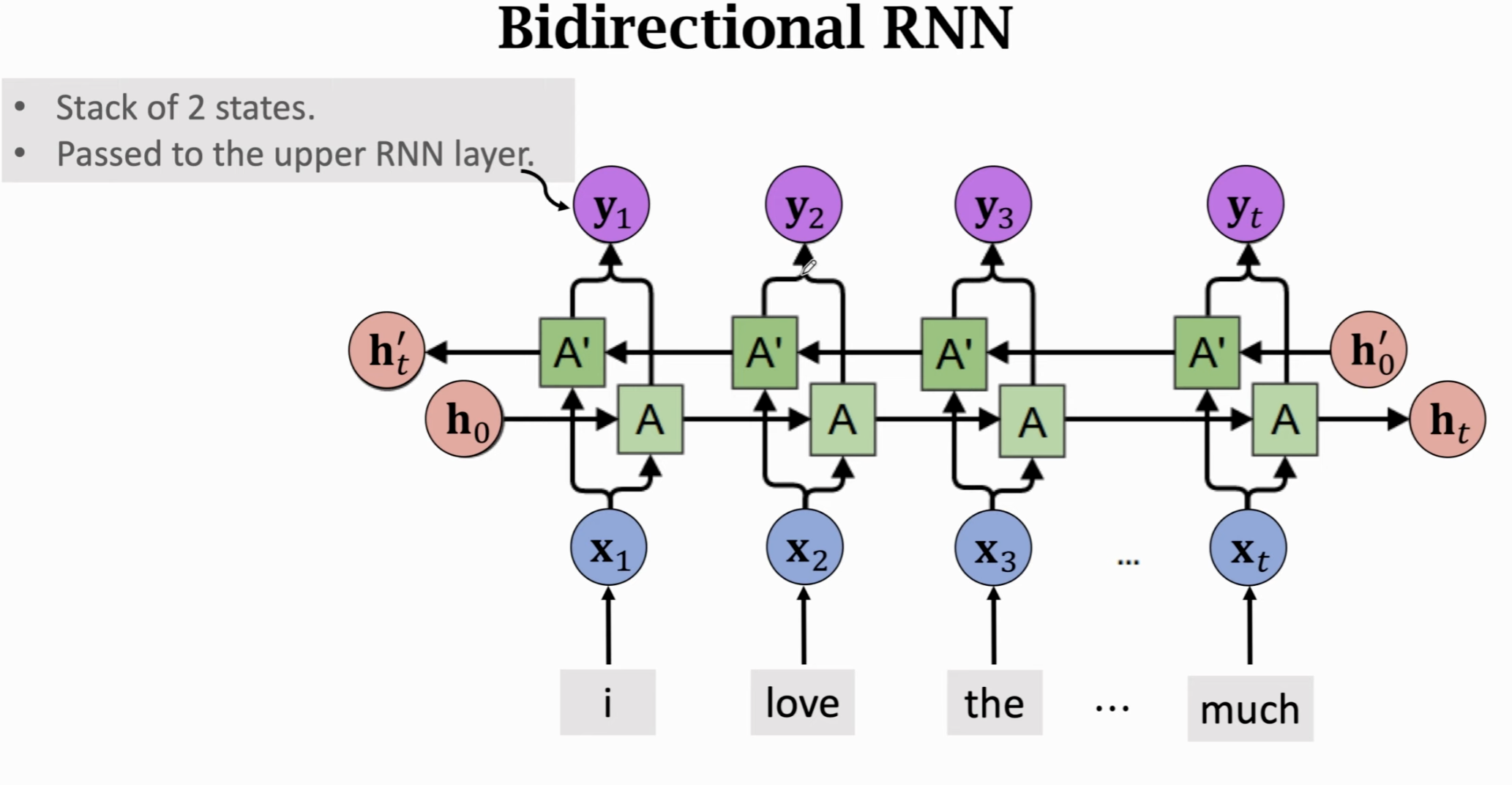
一个简单的想法是训练两条RNN，一个从右往左，一个从左往右。两条RNN互相独立==不共享参数，会各自输出对应的状态向量==，两个状态向量 concat 起来就形成了真正的状态向量 \(y_1, y_2, ... , y_t\)。如果有多层RNN，就把输出的 y 作为上层RNN的输入，以此类推。

这个双向RNN的输出，就是把两条RNN分别走到最后输出的向量 \(h^{'}_t, h_t\) 做一个concat，成为这段文本的特征向量。

一般而言，双向RNN效果比单向的要好很多，因为从一个方向阅读容易忘记前面的，现在可以比原先的特征多记住一些信息了（一个记得更靠左边的，一个记得更靠右边的）。

我们可以发现参数量就是单层的2倍。

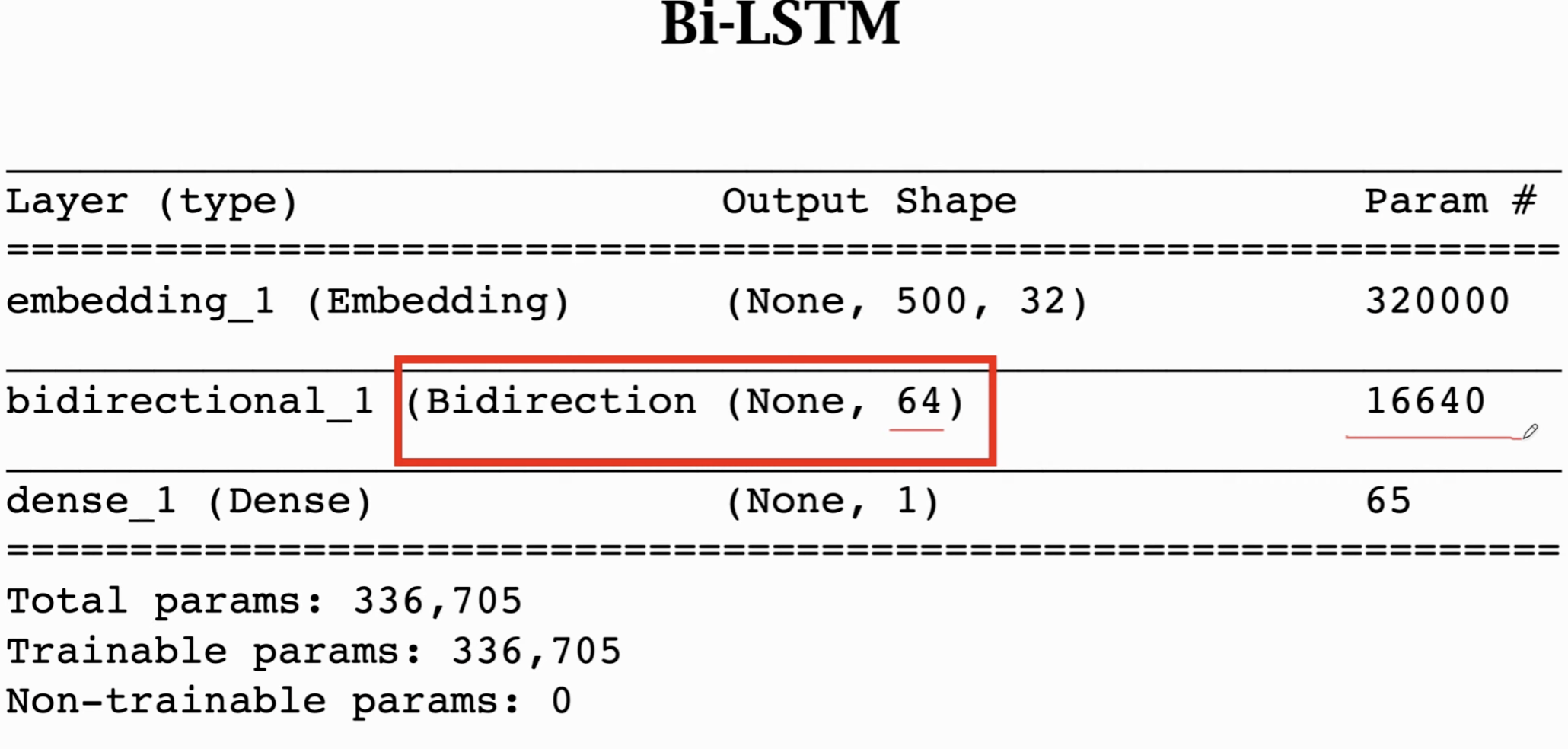
实际做的时候，两种方法都试试（双向+stack）。

预训练⚓︎

Pretrain。一种非常常用的技巧。在CNN里就有涉及。比如你的训练集不够大，但是参数又很多，于是你可以先在一个更大的数据集上训练一个模型，让神经网络有比较好的初始化参数（尤其是embedding），避免overfitting。

具体做法：

找一个更大的数据集（最好是接近原先的任务，比如情感分析）；
搭建并训练一个大的神经网络；
只保留embedding和对应参数，训练上层的参数；embedding这部分的参数固定住不需要训练

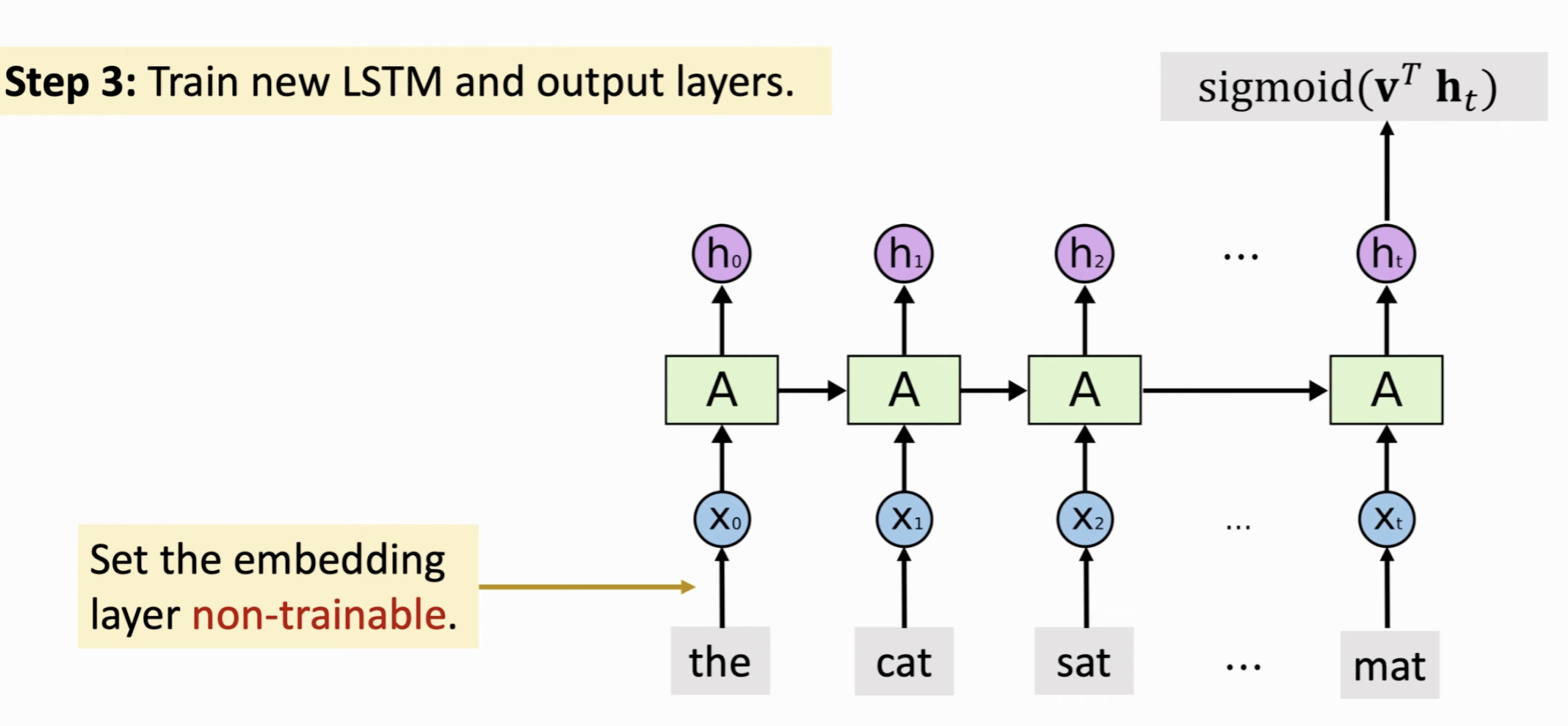
这类问题用LSTM效果往往会好一些，应用时候可以多试试不同的结构，比如Stacked Bi-LSTM等。这几个Idea对所有的RNN都适用。而且LSTM能记住更多信息，不容易遗忘

自动文本生成⚓︎

输入半句话，要求预测下一个字符。可以训练神经网络，用one-hot embedding来表示每个字符，在大量文本上以字符维度进行训练。最终输出一个向量（用softmax做概率分布）。就可以拿到概率最大的那个字符。

如何训练这个RNN？设置步长stride和每个切片的大小。训练时，需要基于每个切片内的文本，正确给出下一个字符（即为这个字符的概率最大）。此时下一个字符就是label，每个segment就是输入的文本，训练数据就是 (segment, char) 的pair。其实质上就是一个多分类问题（类别数是所有的字符数）。

一些应用：生成名字；这说明文本生成器不是记住数据，而是能够生成新的东西。

SCIGen

简单字符生成器的实现⚓︎

生成字符切片。

由于我们是字符生成，因此总共可能也就几十个字符，不需要做低维的embedding了，直接用one-hot embedding即可。

现在假设每个片段有60个字符，而我们需要输出的字符总共有57个（字典大小），那么每一segment就是 60 * 57 的矩阵。需要进行一个有 57 分类的多分类预测。

具体细节：

输出了每个字符的分布之后，如何选择下一个字符呢？

greedy selection，每次都选择概率最高的那个（选择不够多）
从多项式分布（multinomial distribution）中随机抽取；
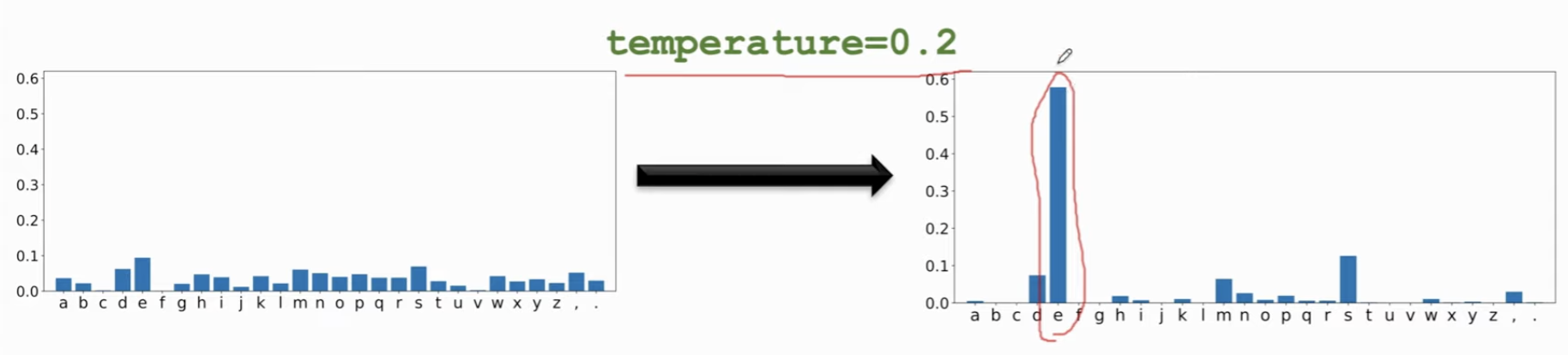
介于前两种之间，有一定随机性，但是不会太大，用temperature （在 0,1之间，对概率值做幂变换，调整概率值，使得大的更大，小的更小）然后再归一化

s既然是文本生成器，必须要先给他说些什么，开个头。让他接着生成。假设固定一个片段长度为 18 字符（Token）。最初的片段称为seed。这个18字符的片段做one-hot embedding，形成矩阵，把这个矩阵输入神经网络，抽样，生成下一个字符；生成之后，把新的字符加入片段，同时删除最开始的第一个字符，这样保证新的片段依然是 18 字符（token）长的。

想要生成文本，首先需要训练一个RNN。

划分片段成 (seg, next_chair) 的二元组；
embedding （one-hot/embedding），此时 char = \(v \times 1\), seg = \(v \times l\), l 为 seg 长度
训练神经网络（matrix - LSTM - Dense - vector）

Seq2Seq 模型（机器翻译）⚓︎

机器翻译是一个多对多的问题，英文长度 > 1，要翻译的语言的长度 > 1，输入输出长度不固定。

Tokenization & Build dictionary⚓︎

要准备两套字典，一套是被翻译的语言，一套是要翻译语言的。又分为 word-level 和char-level，一般是 word-level，把一句话分成很多的单词构成 token。

需要两套词典的原因：

语言有不同的字符表，尤其是word-level tokenization。

One-hot encoding⚓︎

以 char-level 的模型为例，一句话的每个字符都可以被映射到原先字典里的一个数字。这样，每句话就可以用一个矩阵来表示。这个矩阵就是 RNN 的输入。

其实你用词向量在word level进行操作，效果和这个差不多，只不过不是 one-hot的了，而是一个定长向量；

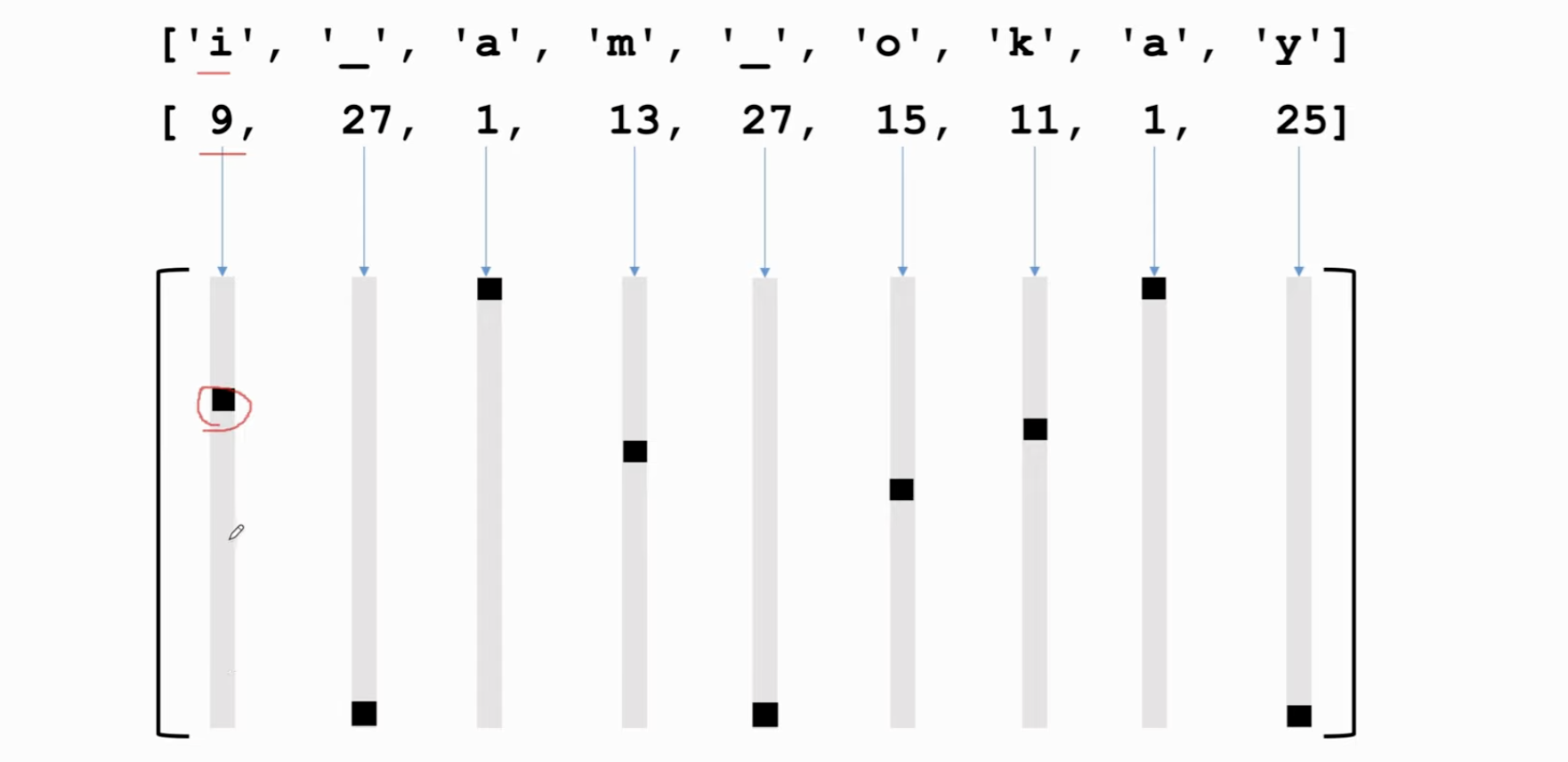
Train seq2seq⚓︎

由一个 Encoder 和一个 Decoder 组成。

Encoder 是一个 LSTM 或者其他 RNN，用于从输入的句子中提取特征，其最后一个状态，就是从输入状态提供的特征，包含这句话的信息，其余的状态没有用。

如果你的 Encoder 是一个 LSTM，那么输出的就是最后一个Token时候的状态向量和传送带。

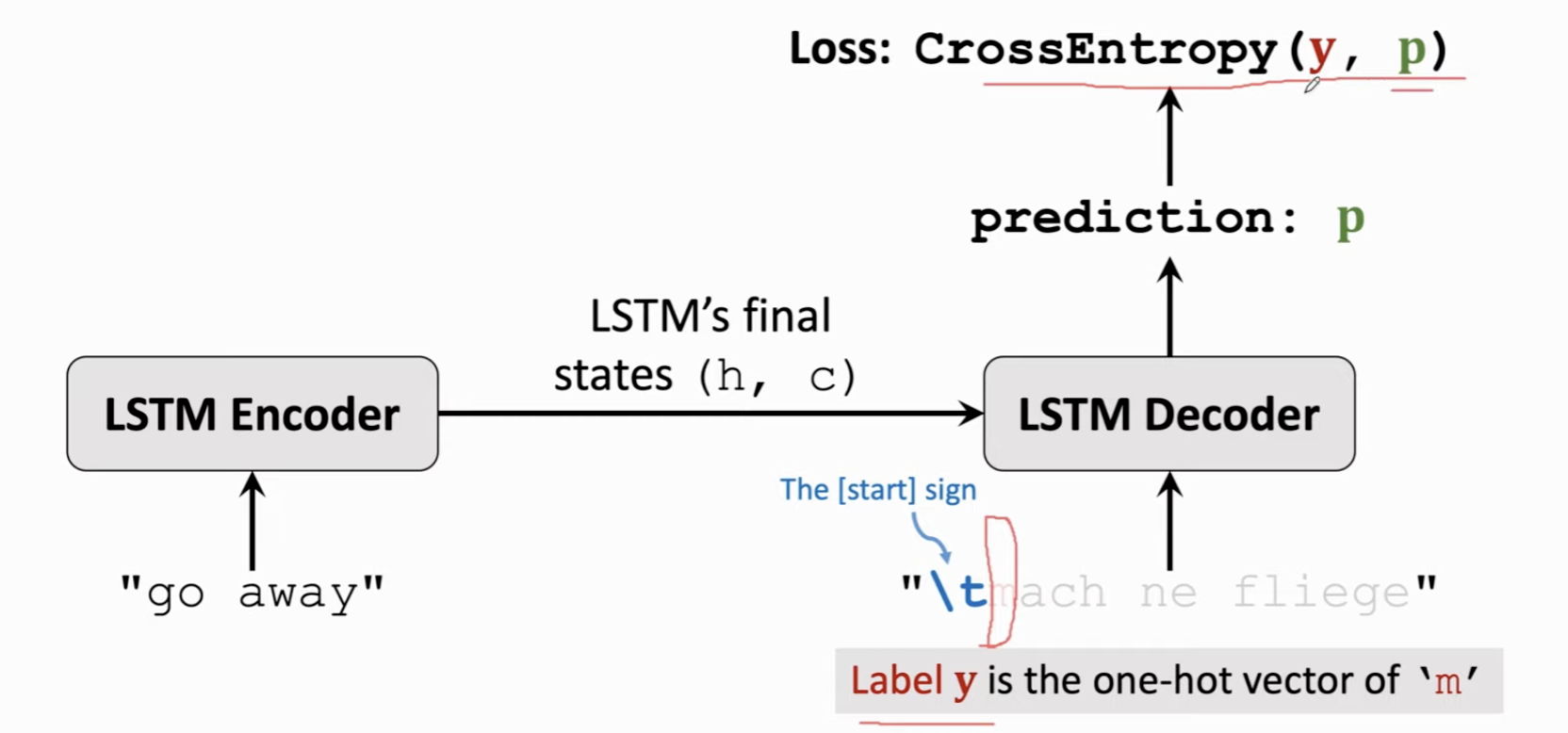
在 Decoder 层（也就是翻译成的语言），首先你需要保证这个字典里有起始符。此时我们给它的单词就是这个起始符。Decoder 会输出一个概率分布 \(p\)。

我们知道这句话正确的下一个字符是 m，所以，我们的损失函数就是代表 m 的那个 one-hot 向量 y 和我们输出概率分布的交叉熵。

通过损失函数反向传播计算梯度，一直传输（decoder-encoder），从而更新模型参数，让模型参数进行调整。

然后的输入是两个字符，我们要做的是预测更下一个字符，同上所述找 one-hot，计算损失函数，反向传播，以此类推，不断重复，直到这句话的最后一个字符（停止符），我们会把整个被翻译好的句子输入，希望模型能输出停止符。

上述这个过程是对一个 英语-德语 二元组进行计算的结果，事实上你的数据集里有非常多的这种二元组，你需要把这些数据丢进来进行训练。你训练的过程实际上就是调整这些参数矩阵，使得输入一个英文句子后，输出的翻译句子与实际正确翻译的句子的差距（交叉熵）尽可能小。

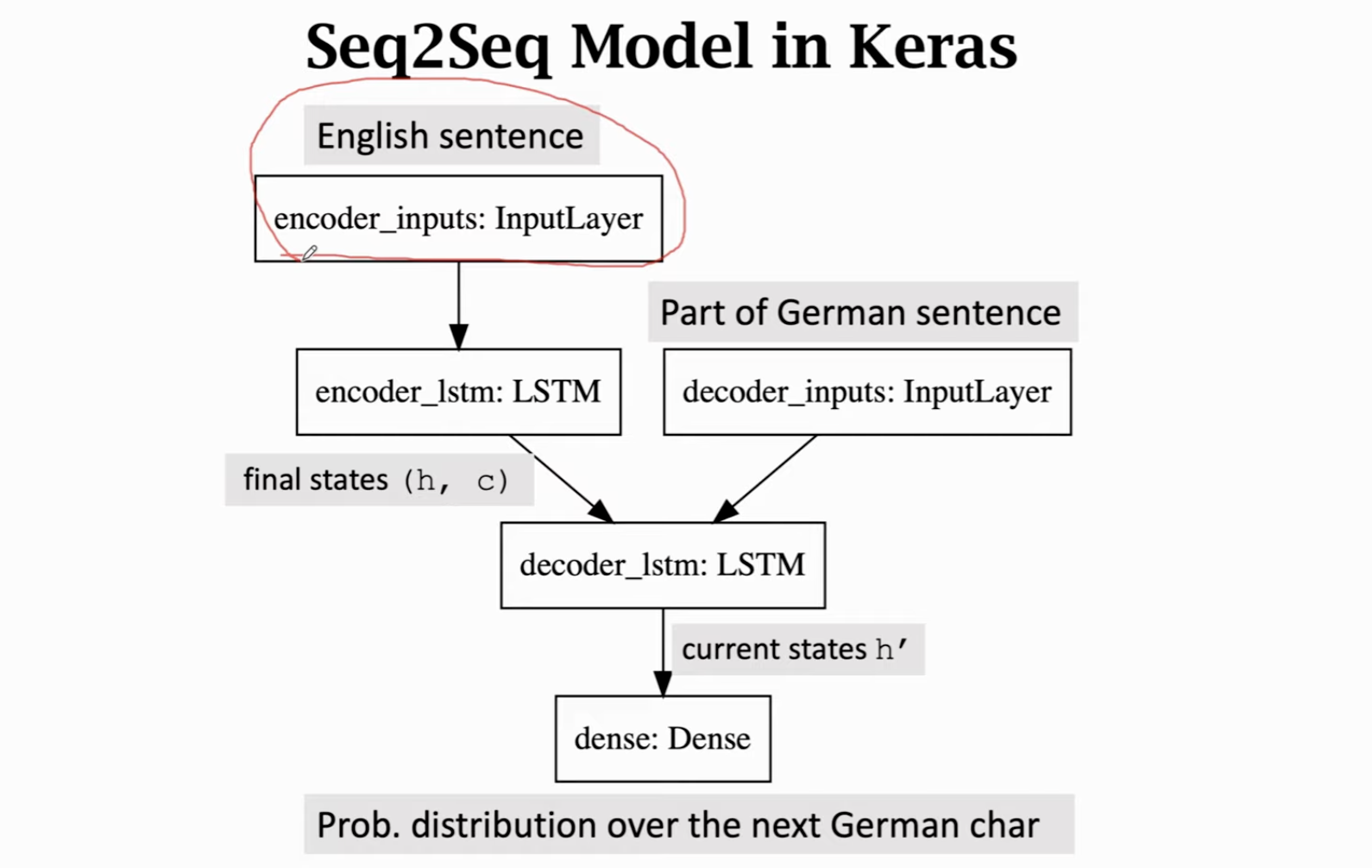
总结⚓︎

Seq2Seq做机器翻译，输入句子的时候，Encoder会在每输入一个词的时候更新状态，把输入信息记录在Encoder状态里，最后一个状态就是提取的特征。最后一个状态作为 Decoder 的初始状态传递给 Decoder，此时 Decoder 就类似一个文本生成器，基于这个 Encoder 开的头，开始继续向下生成就可。

这里的\(A\) 是 RNN Encoder 的参数矩阵； \(B\) 是 Decoder 的参数矩阵，\(s_1\) 就是基于输入生成的状态向量，这个向量输入全连接层输出预测概率 \(p_1\)，对概率分布做抽样，得到下一个 Token \(z_1\)，这个 Token 当作下一个时刻的输入，继续在 Decoder RNN 中生成状态向量 \(s_2\)，按照类似步骤，生成再下一个时刻的 Token \(z_2\) ...

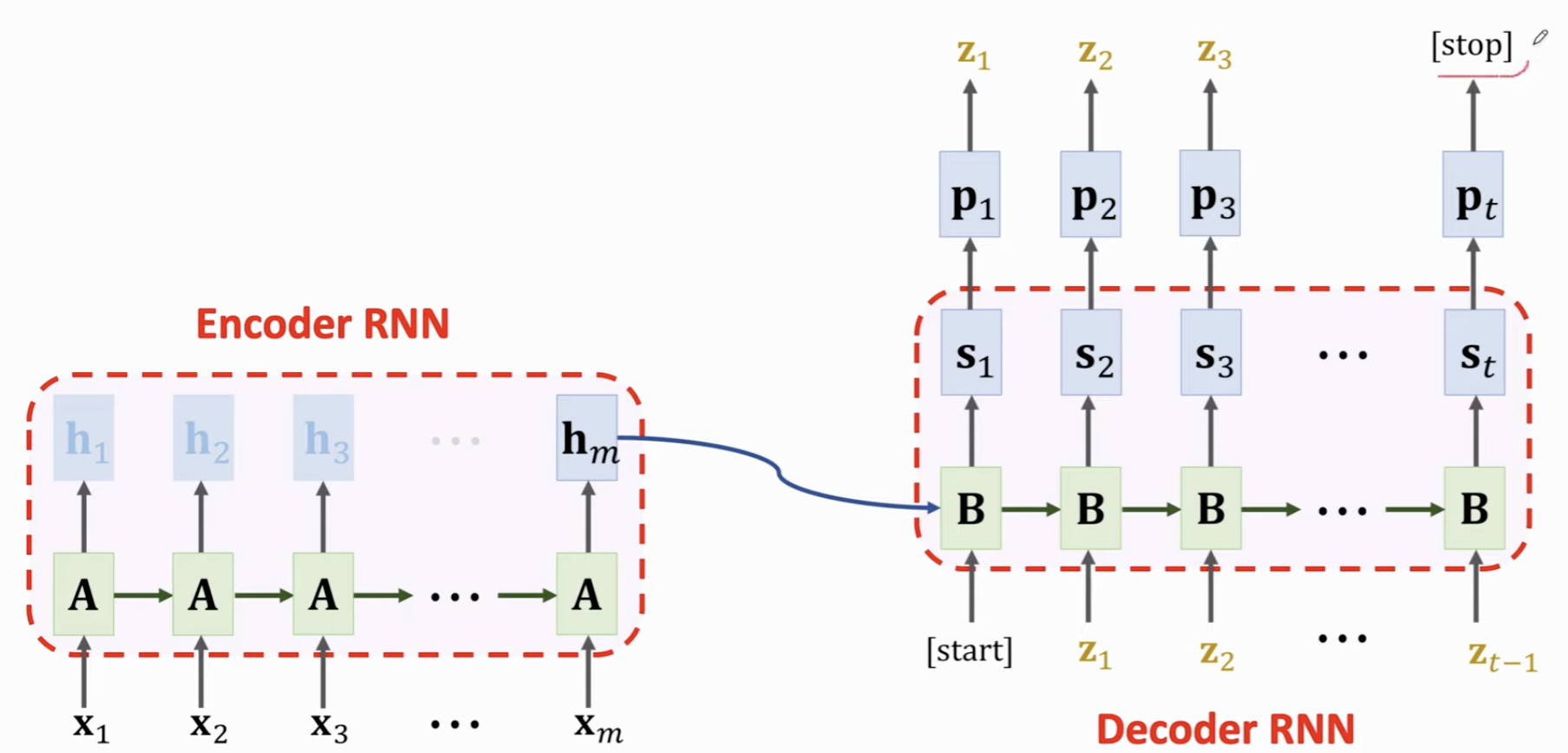
Attention 注意力机制⚓︎

Seq2Seq 模型有一个显而易见的缺陷：无法保证长序列的记忆。 Attention 则可以很好地弥补这个问题。

Attention + Simple RNN⚓︎

在原先的Encoder-Decoder的流程里，总是会丢弃掉Encoder中生成的所有中间状态，而我们现在希望，Decoder 和 Attention同时开始工作，每次Decoder的时候，都会扫一遍原先的文本，去看看有没有哪个（些）Token 与当前的输入的这个 Token 的关联度更高。

这就需要：我们有一种办法来衡量当前这个 Token（向量）和原先那些中间状态（其实就是包含了原先信息的向量）的相似度。

具体做法就是，把每个状态向量用参数矩阵 \(W_k\) 映射到向量 \(k_i\)，每个输入的向量也映射到一个向量 \(q_j\)，计算两个向量的内积 \(\tilde{\alpha_i}\)，然后对输入的句子里的所有内积取softmax映射到 0～1之间。

得到 m 个向量 \(\tilde{\alpha_i}\) 之后，就可以利用这些向量计算每个原先的Token对应的状态向量，其合并起来对当前输入的影响，即计算 Context Vector \(c_j = \alpha_1 h_1 + \alpha_2 h_2 + ... + \alpha_m h_m\)，这个向量长度和状态向量 h 是相同的。

这个 \(c\) 向量记录了encoder中所有Token在当前这个输入Token的完整信息，也就是被这个输入“注意”过后的信息。

此时，我们需要在输出的 RNN 中，计算当前的状态向量 \(s_j\)，此时只需要把原先的最后一个状态向量、Context Vector、当前输入的Token的向量坐concat，然后乘以系数矩阵取tanh，即可得到当前的状态向量了 \(s_j\) 了。

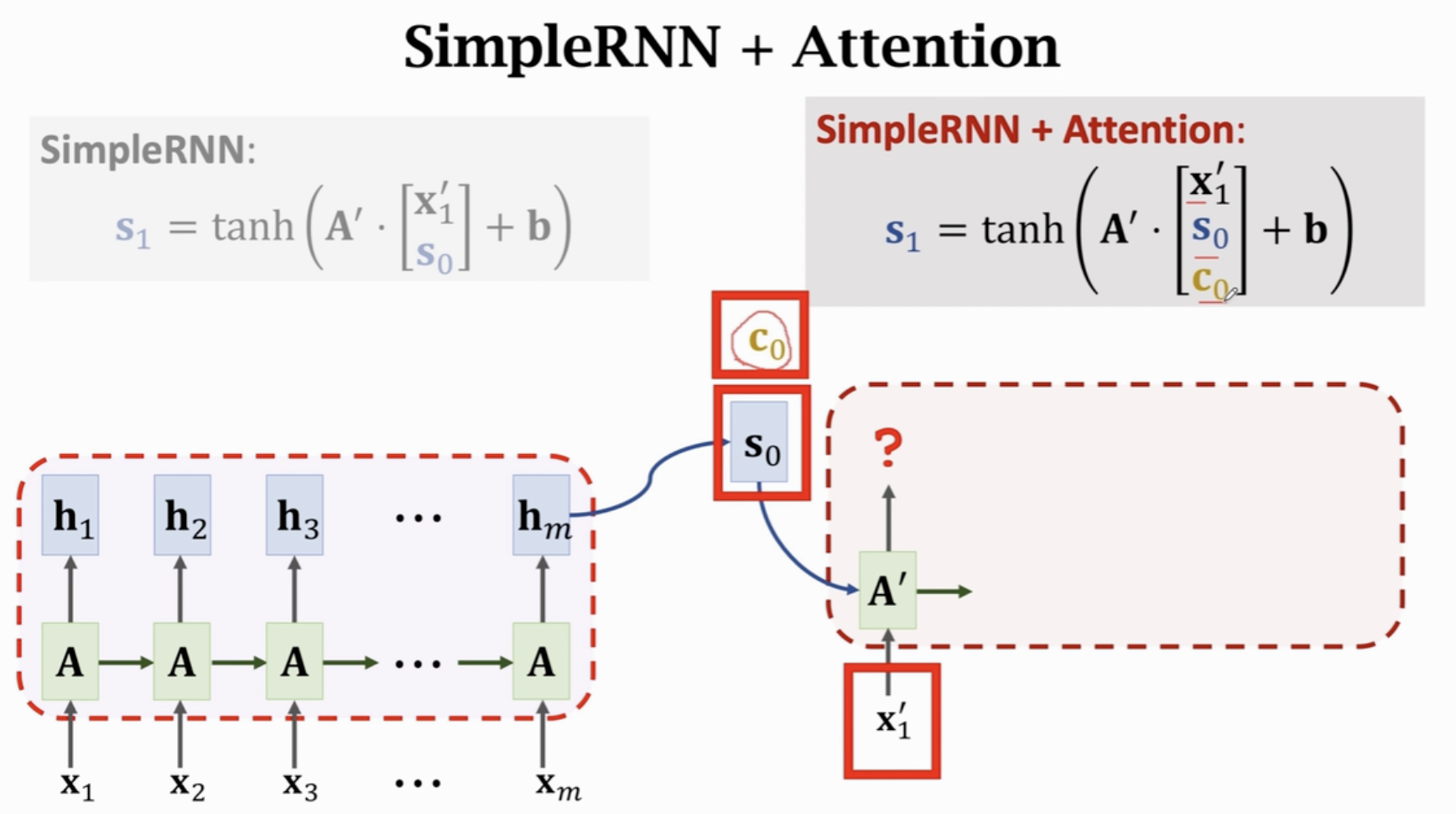
再下一步 \(s_{j+1}\)，只需要将 \(s_j\) 作为前一个状态向量，计算它和 Encoder中每一个 Token 的相似度，构成新的 \(\alpha_i\) ，然后与Encoder中的每个状态向量加权，得到新的 Context Vector \(c_{j+1}\)，拼起来，然后乘以系数矩阵取tanh，即可得到当前的状态向量了 \(s_{j+1}\) 了。

虽然上一轮计算时候有一系列 \(\alpha\)，但是这些 \(\alpha\) 在不同 Decoder 的 Token 下是不同的。

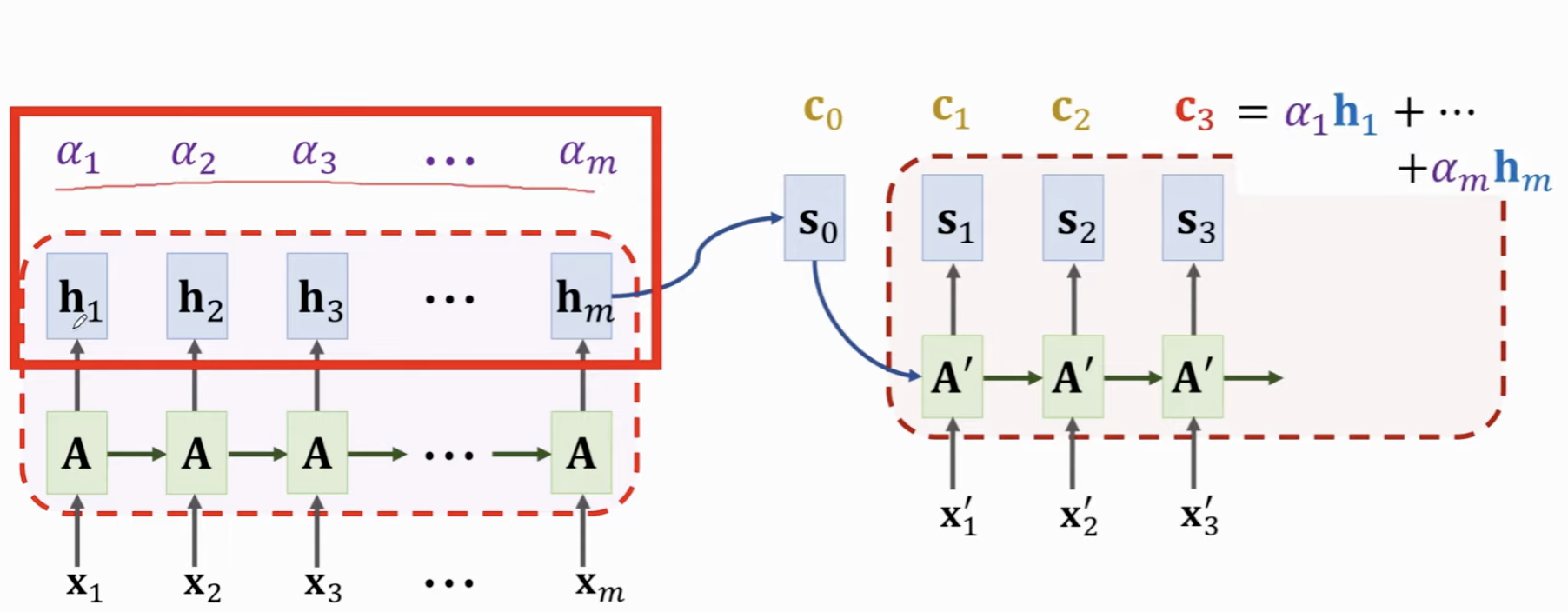
简单来说，要计算 Decoder \(x_4\) 这个 Token 对应的状态向量，需要用到 \(x_4, s_3, c_3\) 这三个部分，分别代表当前 Token 的 Embedding，Decoder 目前最后一个 Token 的状态，以及 Decoder 目前最后一个 Token 在 Encoder 中，经过注意力“注意”后，带有全部 Encoder 信息的 Context Vecotor。

而有了这个 Token 的状态向量后，又可以计算出这个 Token 的 Context Vector，供再后面的使用。

复杂度计算：你可以发现，在每一个 Decoder 的状态下，都需要计算这个状态和 每个 Encoder 状态的 Context Vector，其复杂度 \(O(mt)\)

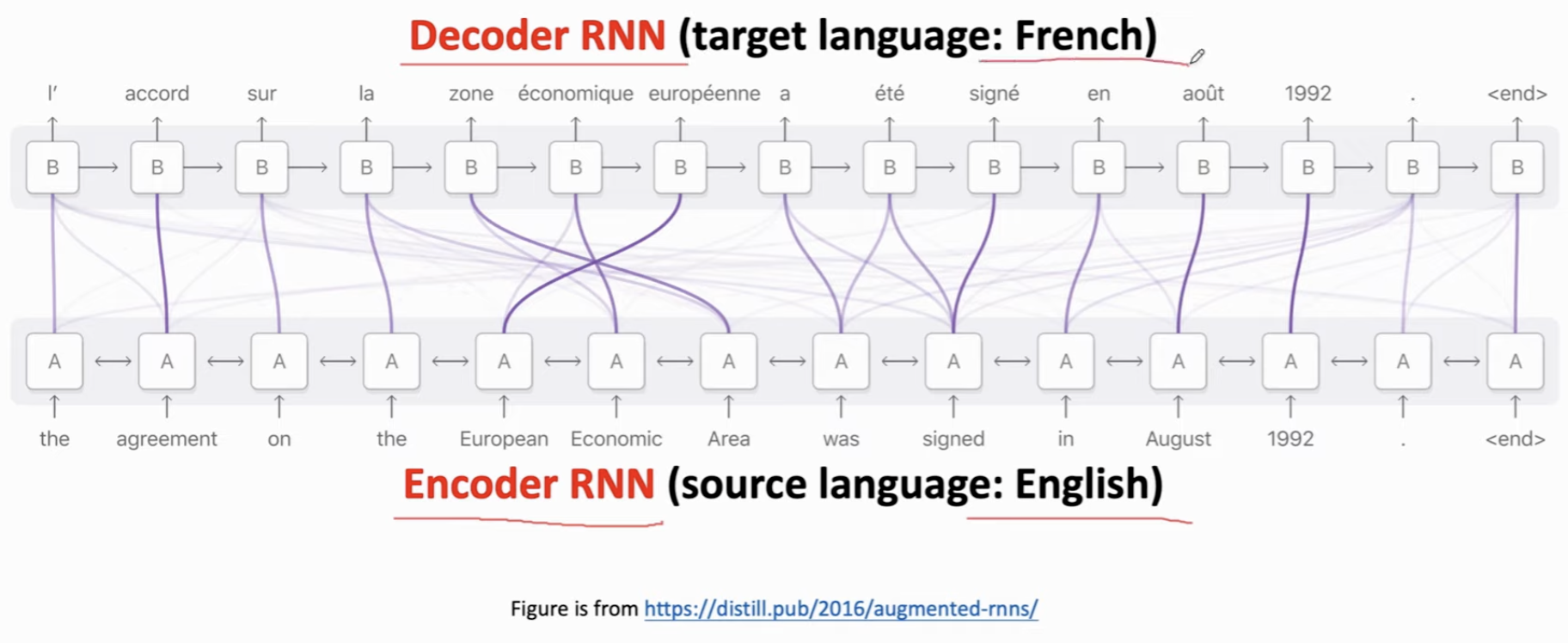
Attention 的可视化，也就是，通过这种 Attention，可以发现某些 Token 之间的相关性（粗表示相关度很高）。

在翻译场景下：Encoder 是英语，Decoder 输出的是法语。每次翻译的时候，遇到一个法语单词，都会看一遍所有的英文单词，看它们和这个法语词的“相关度”，或者重要性。这些权重就告诉了Decoder：你应该看什么地方。

总结：

传统的seq2seq只看当前状态；
Attention可以看到和 Encoder 中所有状态的关联；
Attention通过关联，可以知道重点在哪里；
代价是计算复杂度。

Self-Attention⚓︎

把 Attention 用在一个 RNN，而不是seq2seq的两个 RNN 上。

Step 1.Step. 2Step. 3Step. 4

初始化 \(h_0\) 和 \(c_0\) 均为 0 向量；

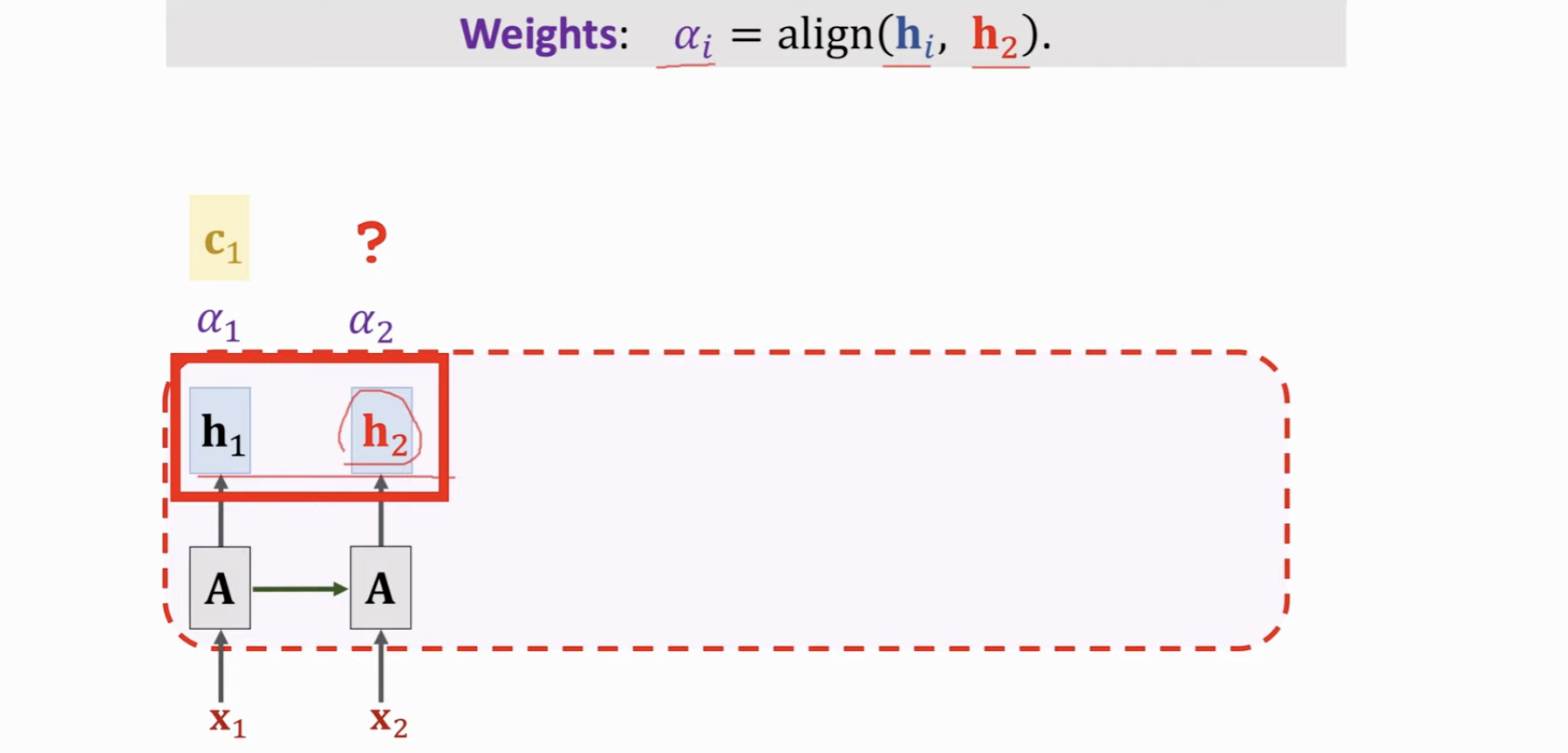
计算当前状态向量时，把原先状态向量替换成 Context vector \(c_{j-1}\)

为了输出 \(x_3\) 的状态向量，我们需要用 \(h_2\) 与包括它自己在内的先前所有状态向量进行 Attention 计算，得到 Context Vector \(c_2\)，基于 \(x_3\), \(c_2\) 得到。

计算顺序是：先有了 \(h_2\)，然后计算 \(c_2\)，结合 \(x_3\) 才能算出 \(h_3\)

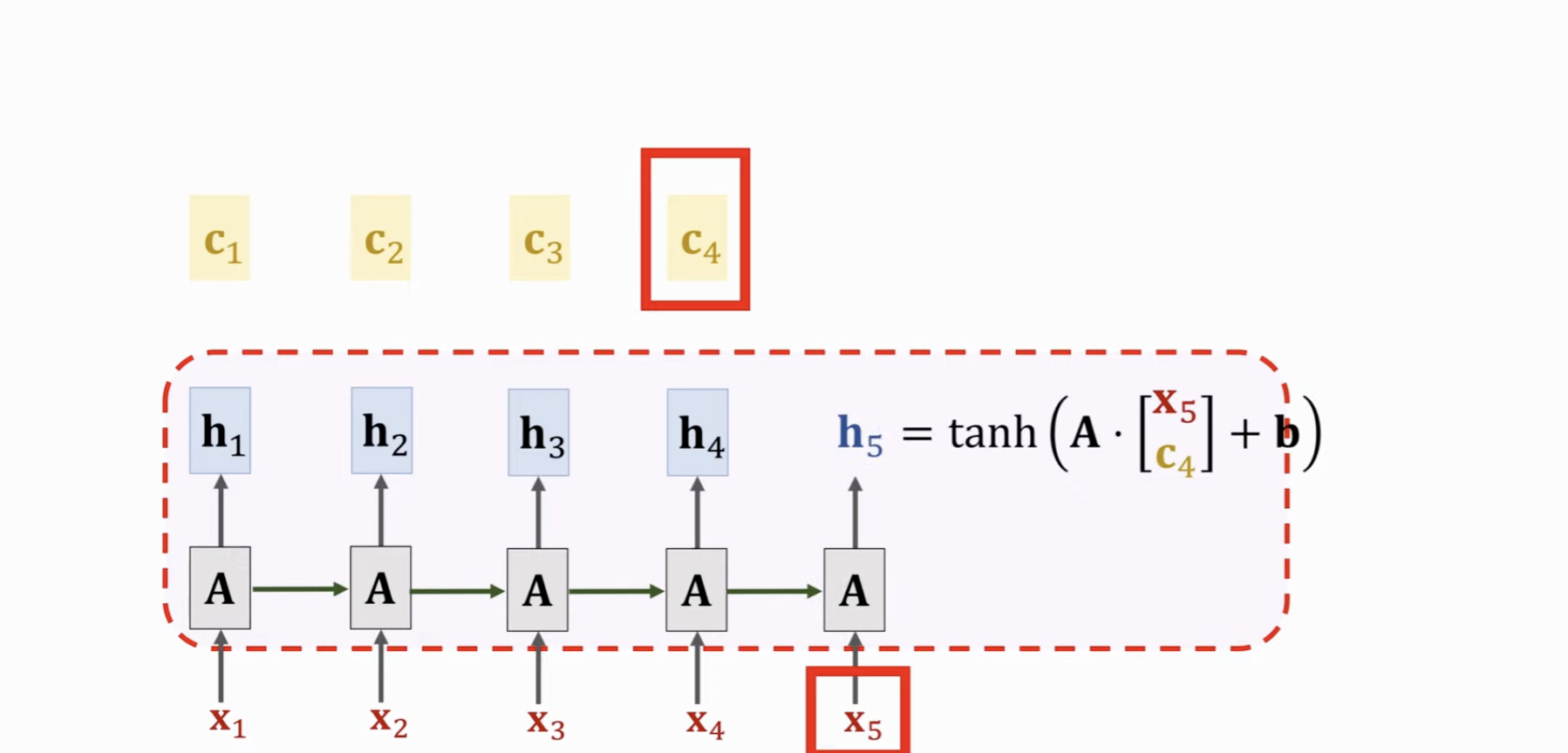
通过 Self- Attention，更加不容易遗忘，同时能够关注最相关的信息。

Transformer⚓︎

Seq2Seq， Encoder + Decoder
不是 RNN，没有循环的结构；
完全基于 Attention 和全连接层。

Attention + Seq2Seq⚓︎

我们首先从保留 RNN + Attention 的模型入手，即Attention + Seq2Seq。这里，我们构造 Context vector 的方式更新了：不再总是用 Encoder 中所有的状态向量和 \(\alpha\) 做加权平均，而是再用一个新的参数矩阵 \(W_V\)，将 Encoder 的每个状态向量都转化成新的 Value 向量 \(v_i\)，对这些 \(v_i\) 向量按照 \(\alpha_i\) 加权平均，得到我们新的 Context Vector。

Attention Layer⚓︎

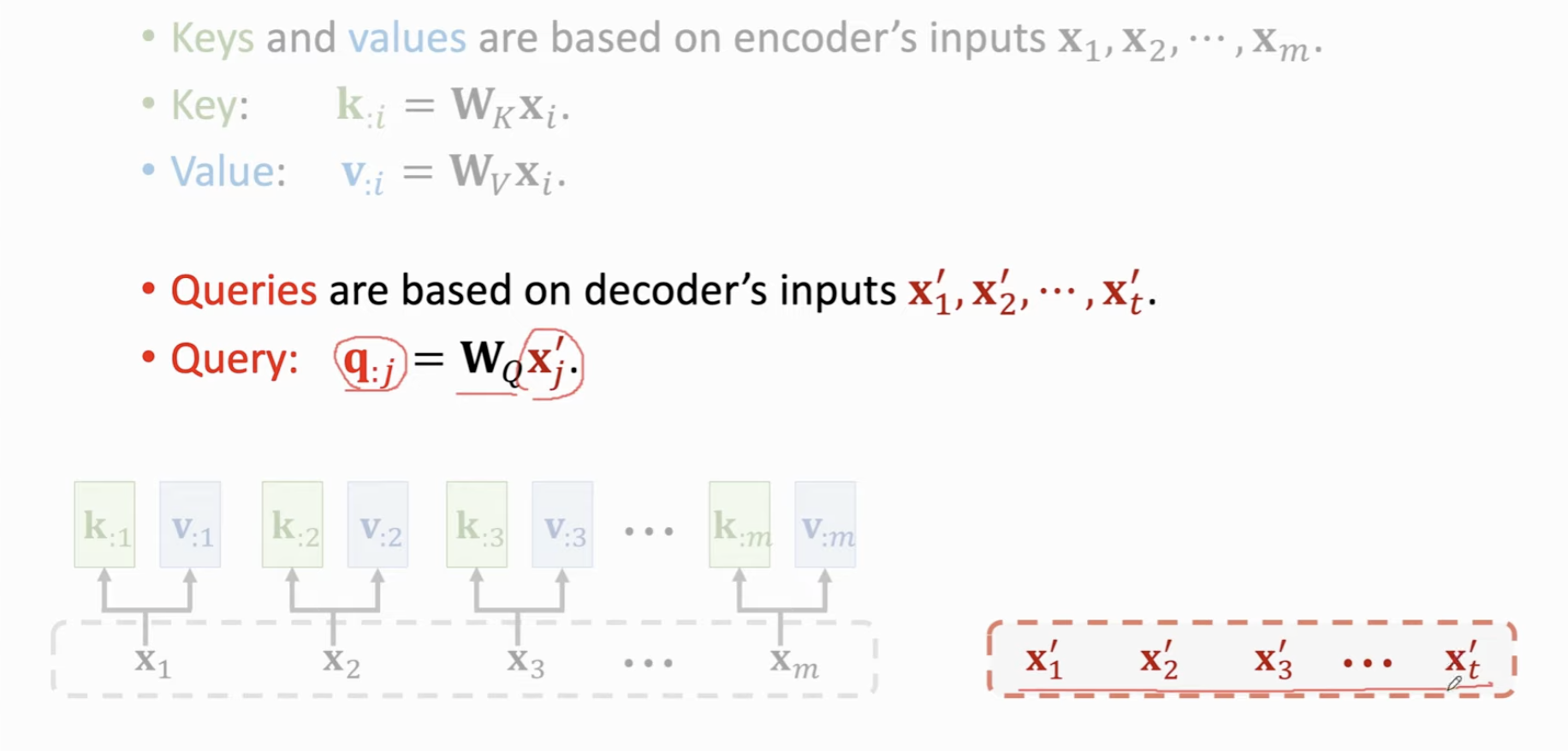
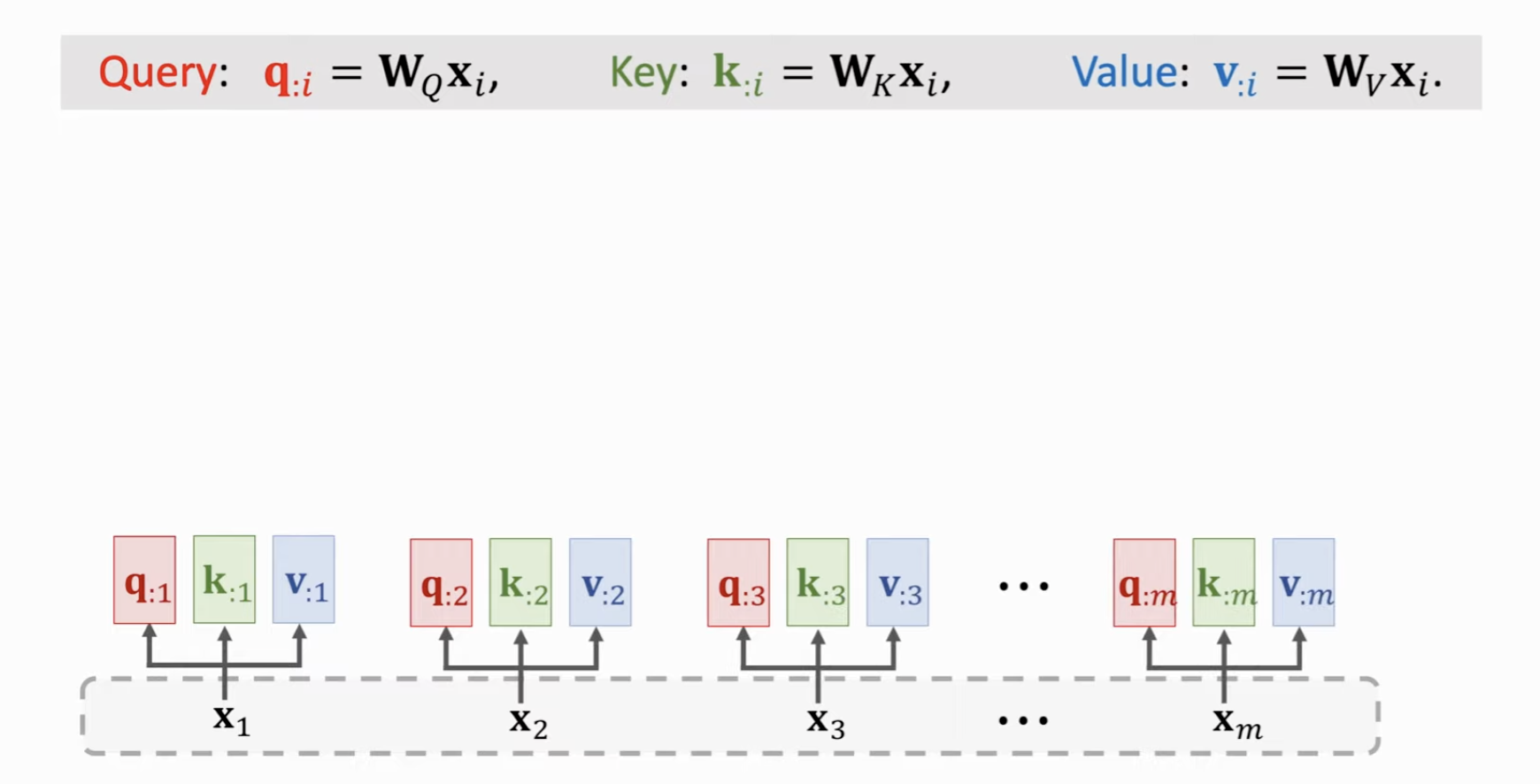
把Encoder的输入计算 Key 和 Value 向量。分别用 \(W_K, W_V\) 进行变换，得到 M 个 \(K\) 向量和 \(V\) 向量，同样地，对于 Decoder 的输入进行类似的线性变换。映射到 \(Q\) 向量。

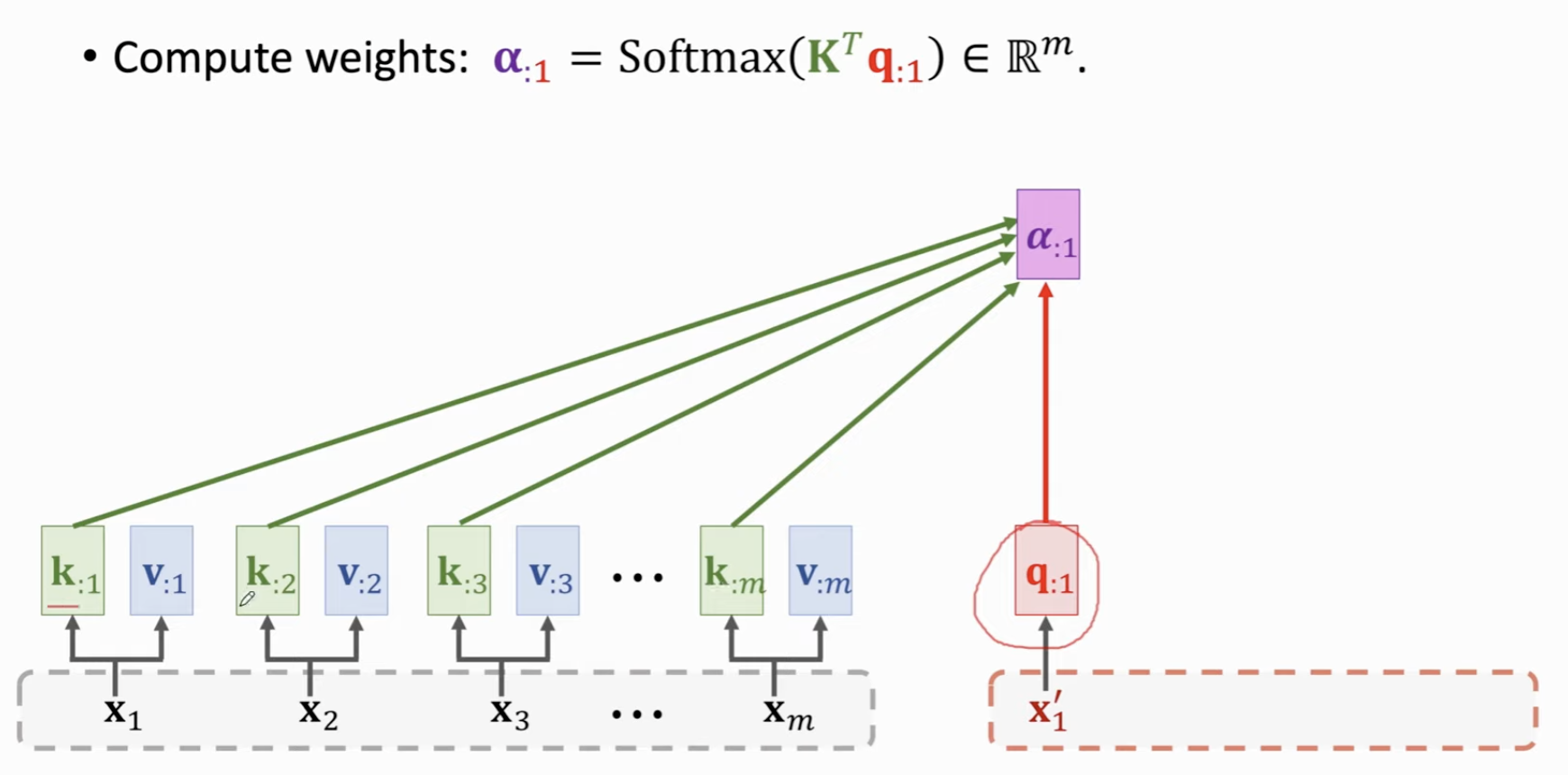
计算权重 \(\alpha\) 时候，用每个 Decoder 的 q 向量与所有的 Encoder 的 k 向量的相关性，计算出 \(m\) 个权重值（经过softmax），得到向量 \(\alpha_1\)。

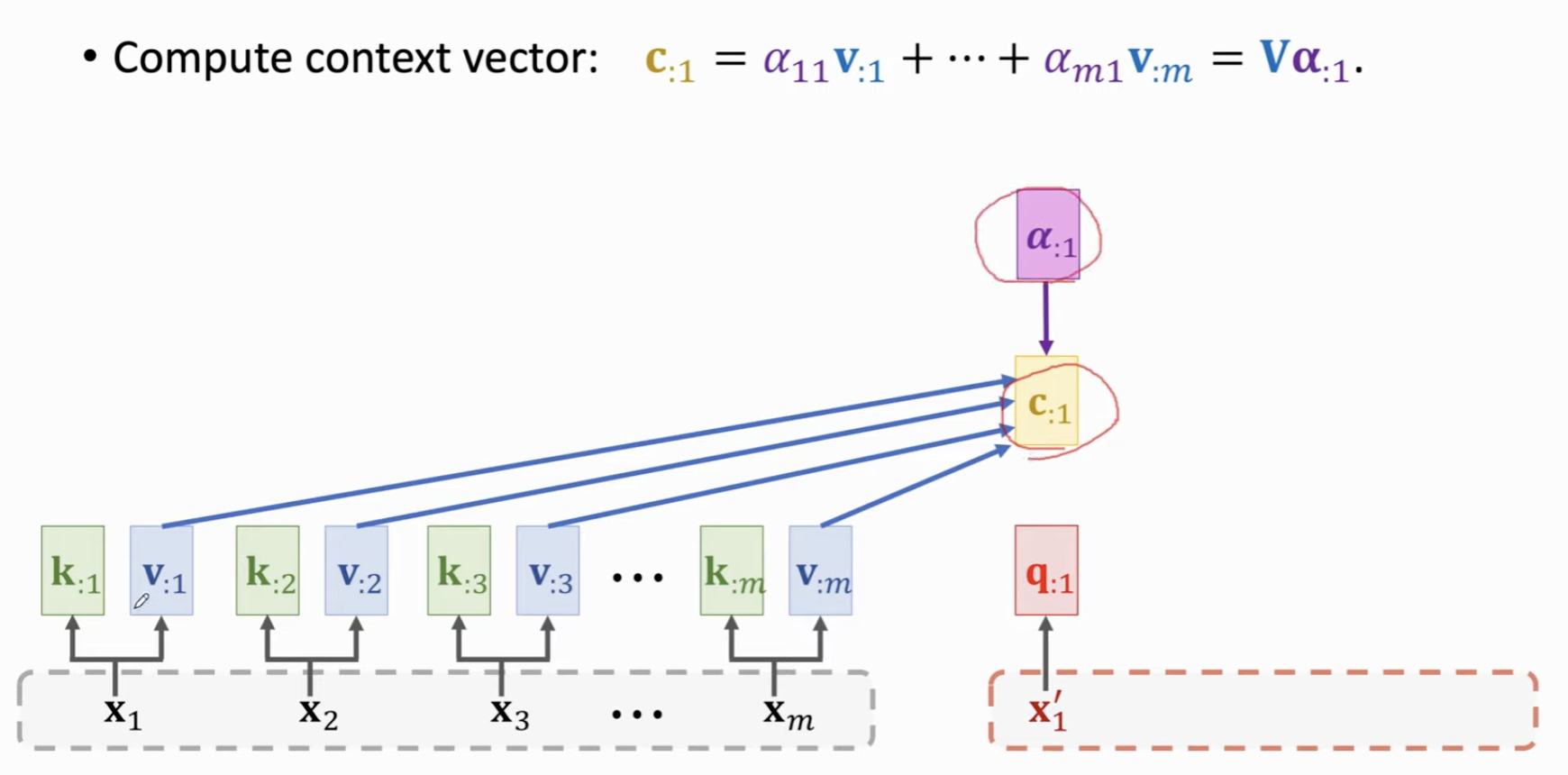
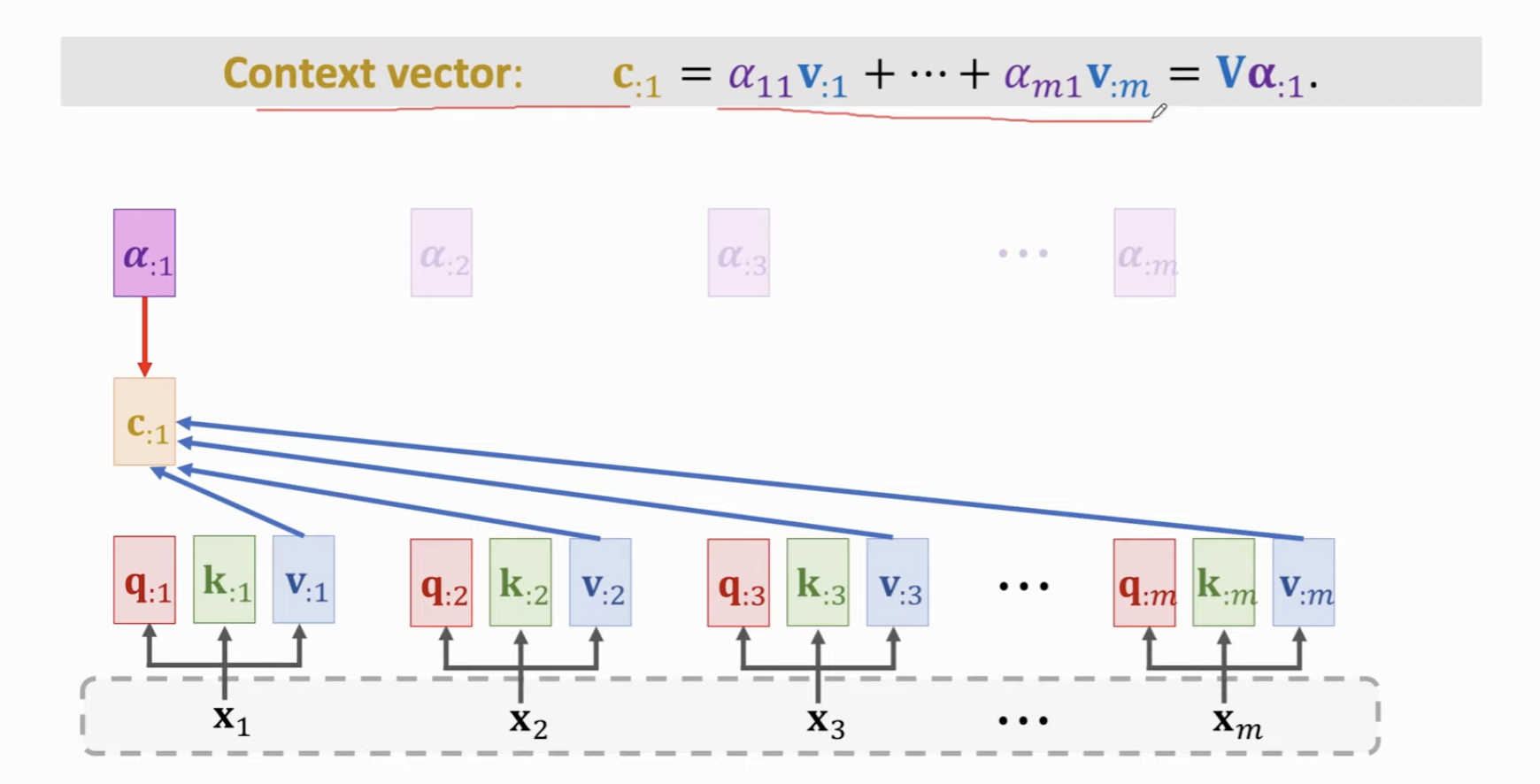
然后计算 Context Vector，做法是用刚刚 \(\alpha\) 向量的每个元素对 Encoder 的每个 \(v\) 向量做加权平均。也就等价于用最大的 \(V\) 矩阵乘以刚刚的 \(\alpha\) 向量。

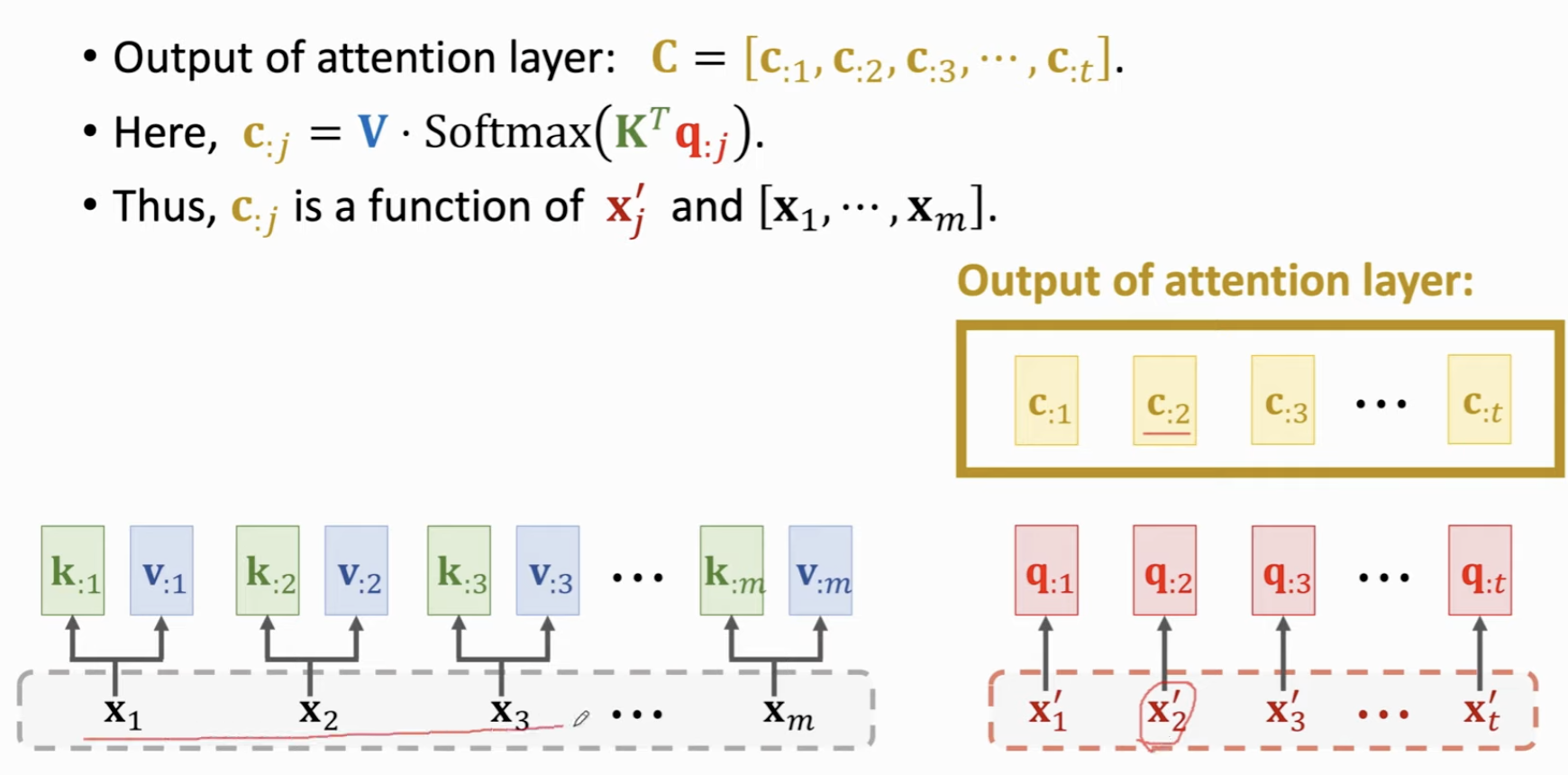
这里，Decoder 有 \(t\) 个 Token，那么就会有 \(t\) 个 c 向量（Context Vector）。

这 \(t\) 个 Context vector 向量 \(c\) 就是 Attention Layer 的输出。

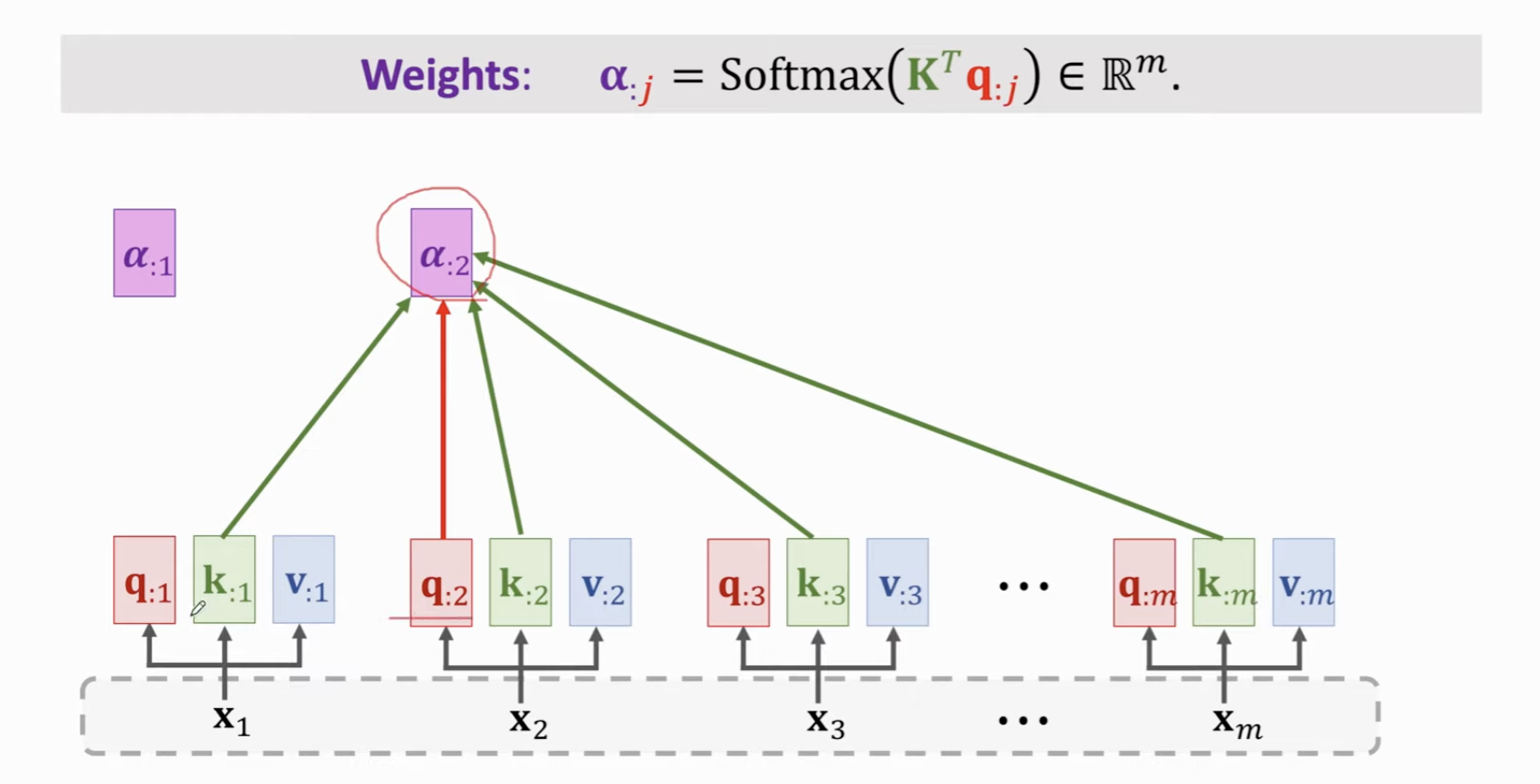
可以看到， \(c_{:j} = V \cdot \text{SoftMax}(K^Tq_{:j})\)

也就是，对于每个 Decoder 中的 Token，想要计算它的Attention层输出的向量，都需要用到原先 Encoder 中每一个 \(K\) 和每一个 \(V\)。这同样意味着，比如在机器翻译中，对于每个翻译后的词 \(x^{'}_j\)，都可以看到原先文本里的每一个文字，看到所有文本中存储的信息。

类似的，既然这个 Context Vector 可以存储如此多的信息，我们可以把它输入一个 SoftMax 分类器，输出每一个词的概率，这个词当作再下一个 Token 文本的输入。和 RNN 用 h 向量作为特征不同，这里用 Context Vector 作为特征向量，涵盖了更多的信息。

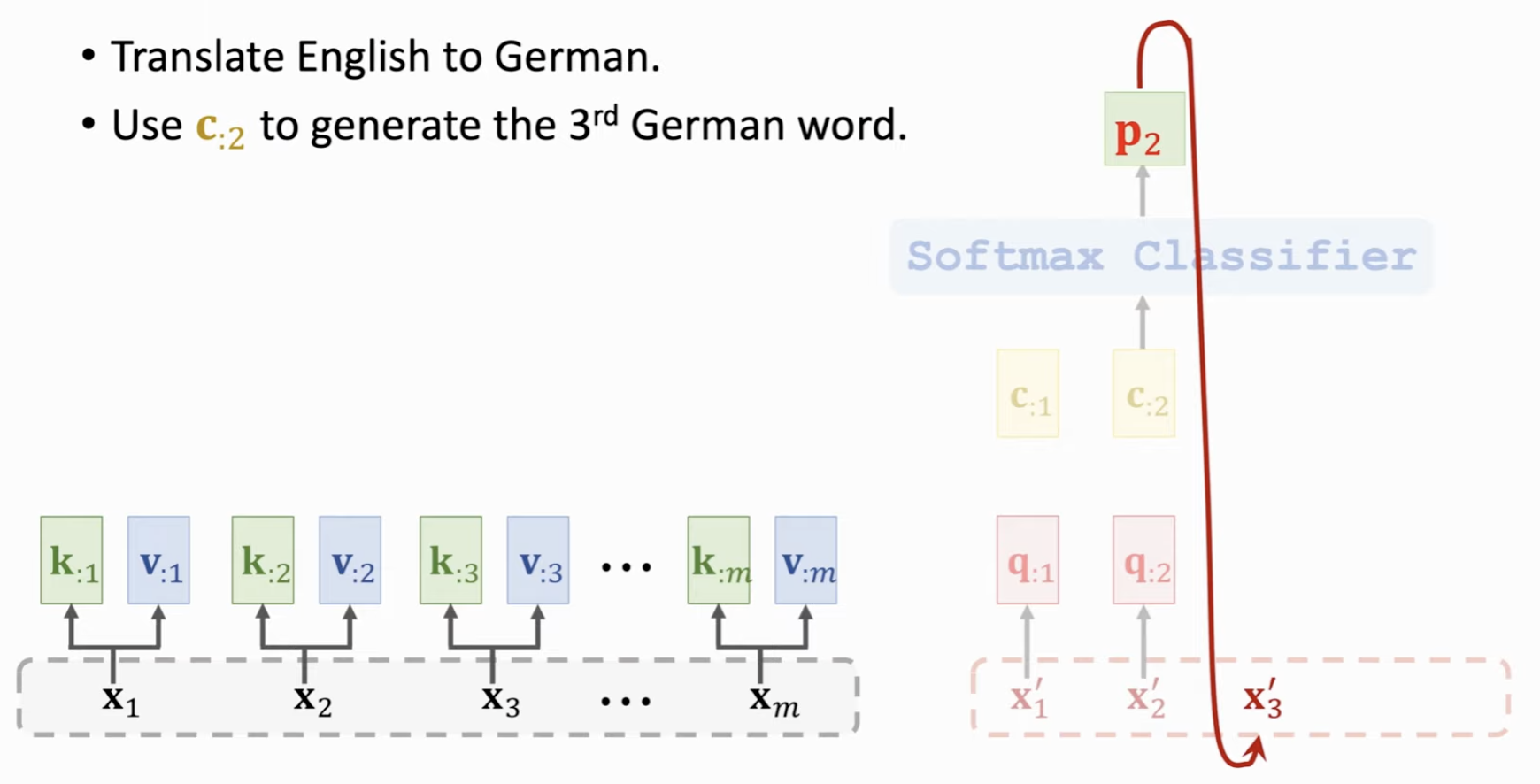
Conclusion⚓︎

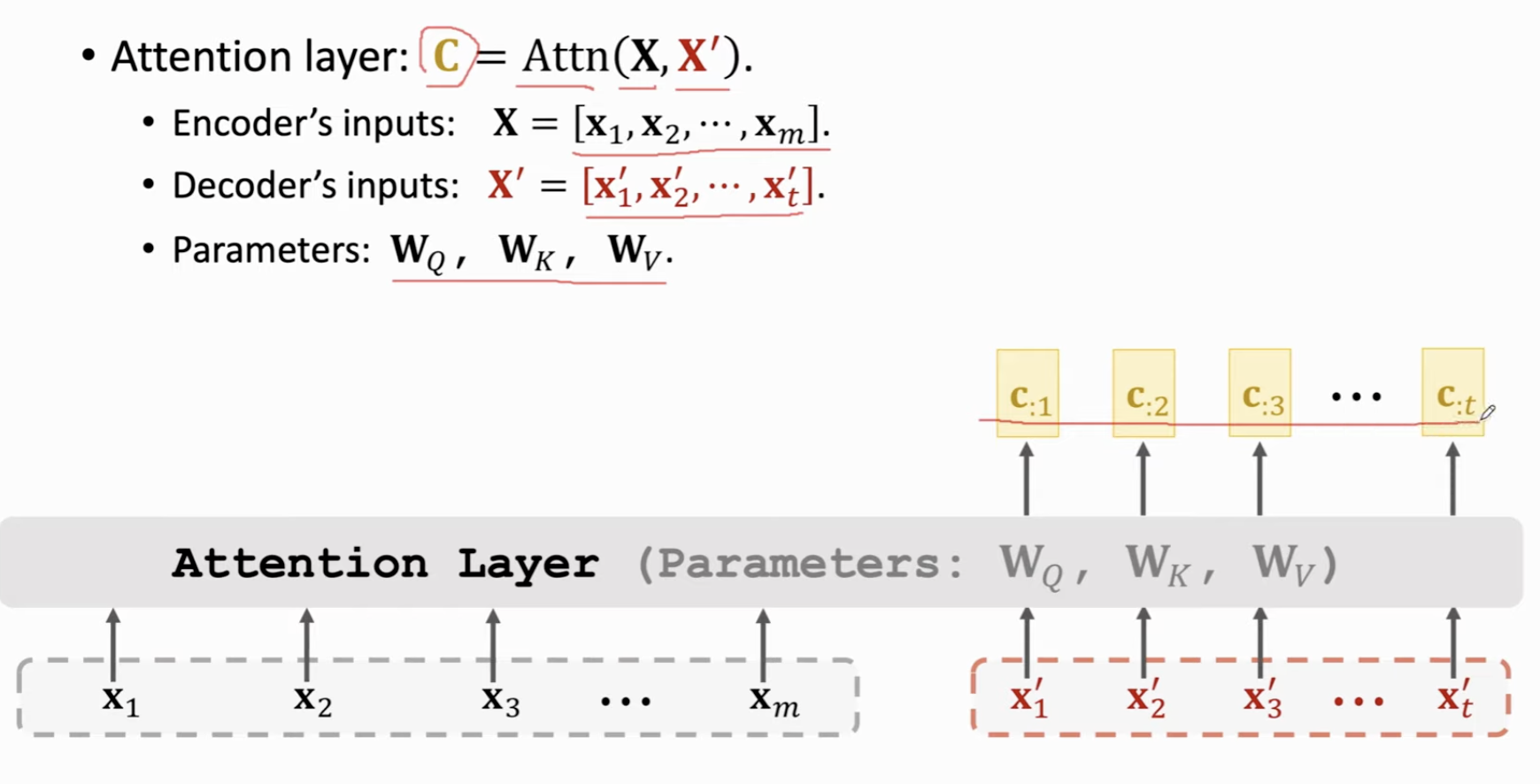
我们可以这样总结一下 Attention 层。

Encoder-Decoder 架构，两组输入 \(X, X^{'}\)。三组需要学习的参数矩阵。\(W_Q, W_K, W_V\)。

Attention层的输出是一个矩阵 C，表示 Context vector。列数和 Decoder 层相同，也就是每个 c 对应一个 \(x^{'}\) 向量。

Self- Attention Layer⚓︎

现在，我们从 Encoder-Decoder 架构中继续脱离，进入 Self-Attention 中，我们只有一个输入了，就是原先 Encoder 中的那个输入（对应机器翻译的待翻译文本）。

Step 1.Step. 2Step. 3Step. 4

做法和前述的几乎一致，区别在于剥离了 Decoder，而 Q, K, V 矩阵都没有变，只不过这三个参数矩阵都作用于同一个输入上了。

计算权重的时候，对于每一个 Token，都需要用到整个文本的所有 K ，以及当前 Token 的 q 向量，然后 SoftMax

得到了每个输入对应的权重向量，对每个Token，计算它和其他所有文本的 V 向量的加权平均（用权重）。如此，得到了输入里每个 Token 的 Context vector。

最后拼再一起，组成 C 矩阵。这就是 Self- Attention Layer 的输出结果。

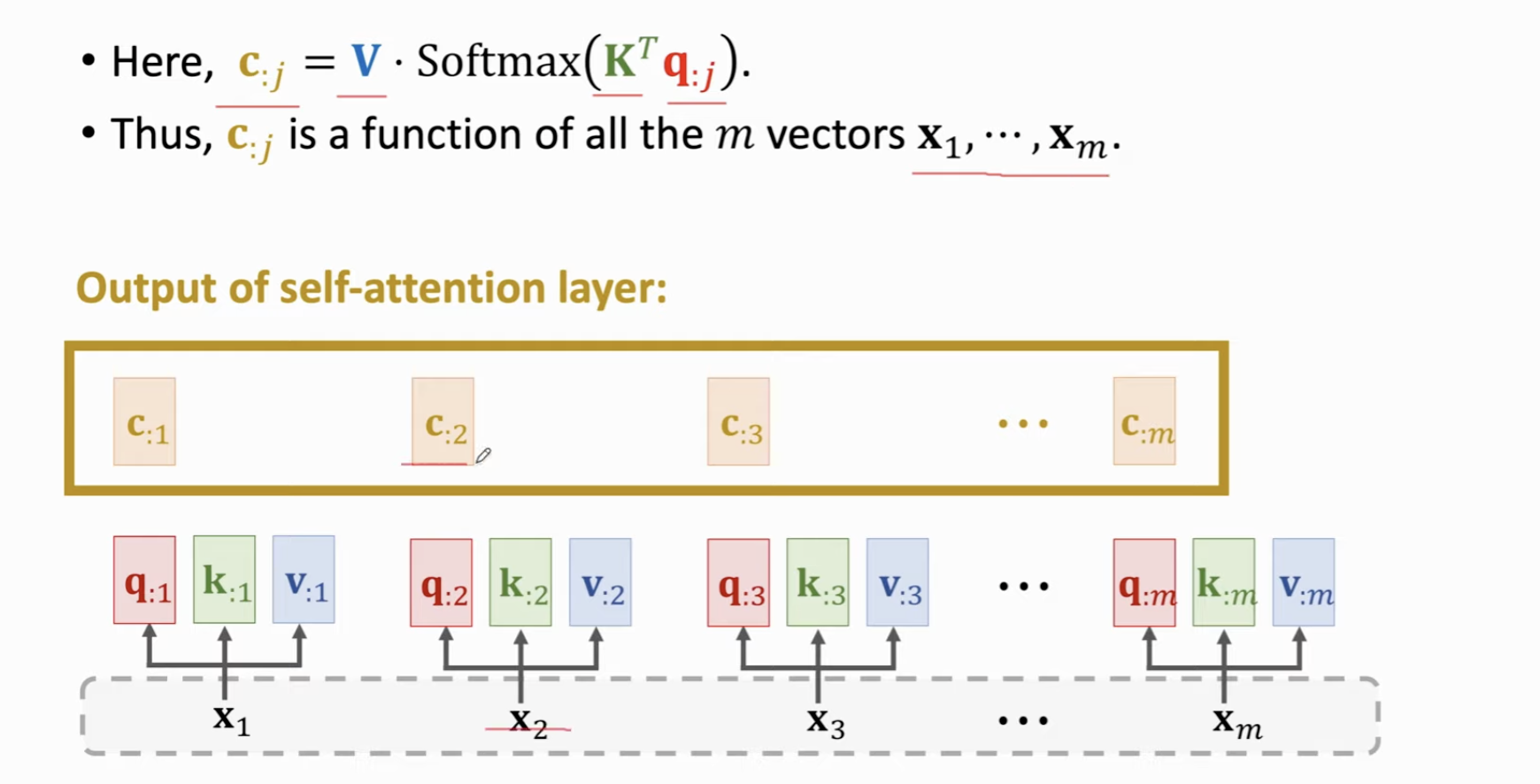
总结一下，Self Attention 的输入是同样的两个 \(X\)，输出是这组向量每个元素对应的 Context Vector。注意，这里的 c 向量其实就可以类比为 RNN 输出的状态向量 h，这两者的大小正好是相同的（都是与该层的输入有关）。由于有 Attention 机制，这里的 c 包含了更多的信息。而正因为它和 RNN 输出的 h 是相同大小的，所以可以直接把 Attention / Self- Attention 层代替 RNN。