LSTM⚓︎
约 6148 个字 9 张图片 预计阅读时间 20 分钟 总阅读量 次
类似RNN的一种循环神经网络,但是要复杂很多。RNN只有一个参数矩阵,LSTM有四个。LSTM 的设计目的在于:
- 减少 RNN 计算中的梯度消失和爆炸;
- 提高对长序列数据的感知,防止遗忘。
传输带 (Conveyer Belt)⚓︎
过去的信息直接通过传输带传送到下一个时刻不会发生太大变化,LSTM就是借助传输带,避免梯度消失的问题。
值得注意的是,传送带实际保存的是细胞状态(cell state),代表了“长期记忆” (Long-Term Memory)。它除了在每个时间步骤下进行乘/加运算,并不会受到其他一些参数(bias,和variance)的影响。正是这个传送带,通过流畅地传导前面的梯度,避免梯度消失/爆炸。
而每一次,和RNN一样保存并计算的Hidden state,就表示了 Short Term Memory。
遗忘门 (Forget Gate, \(f_t\))⚓︎
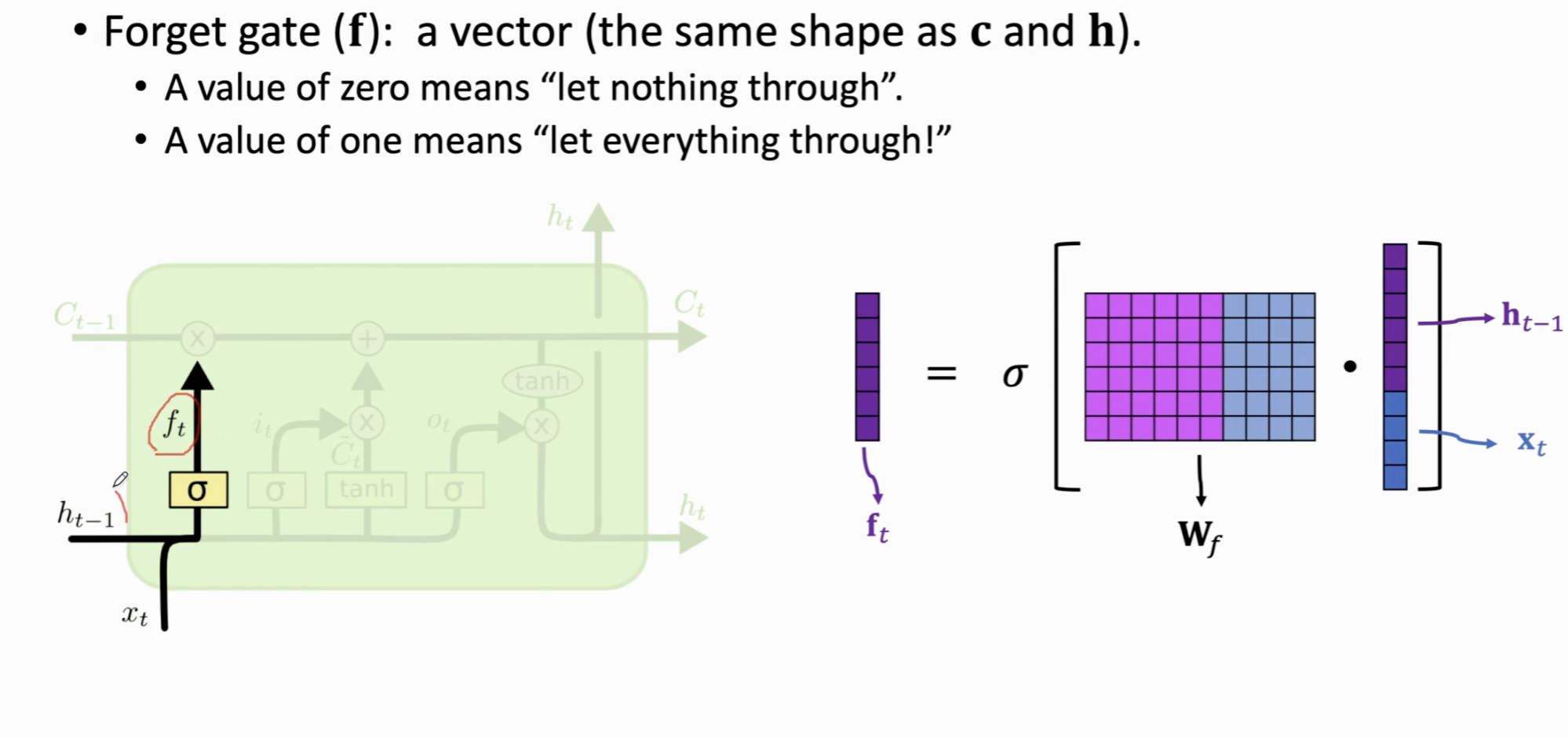
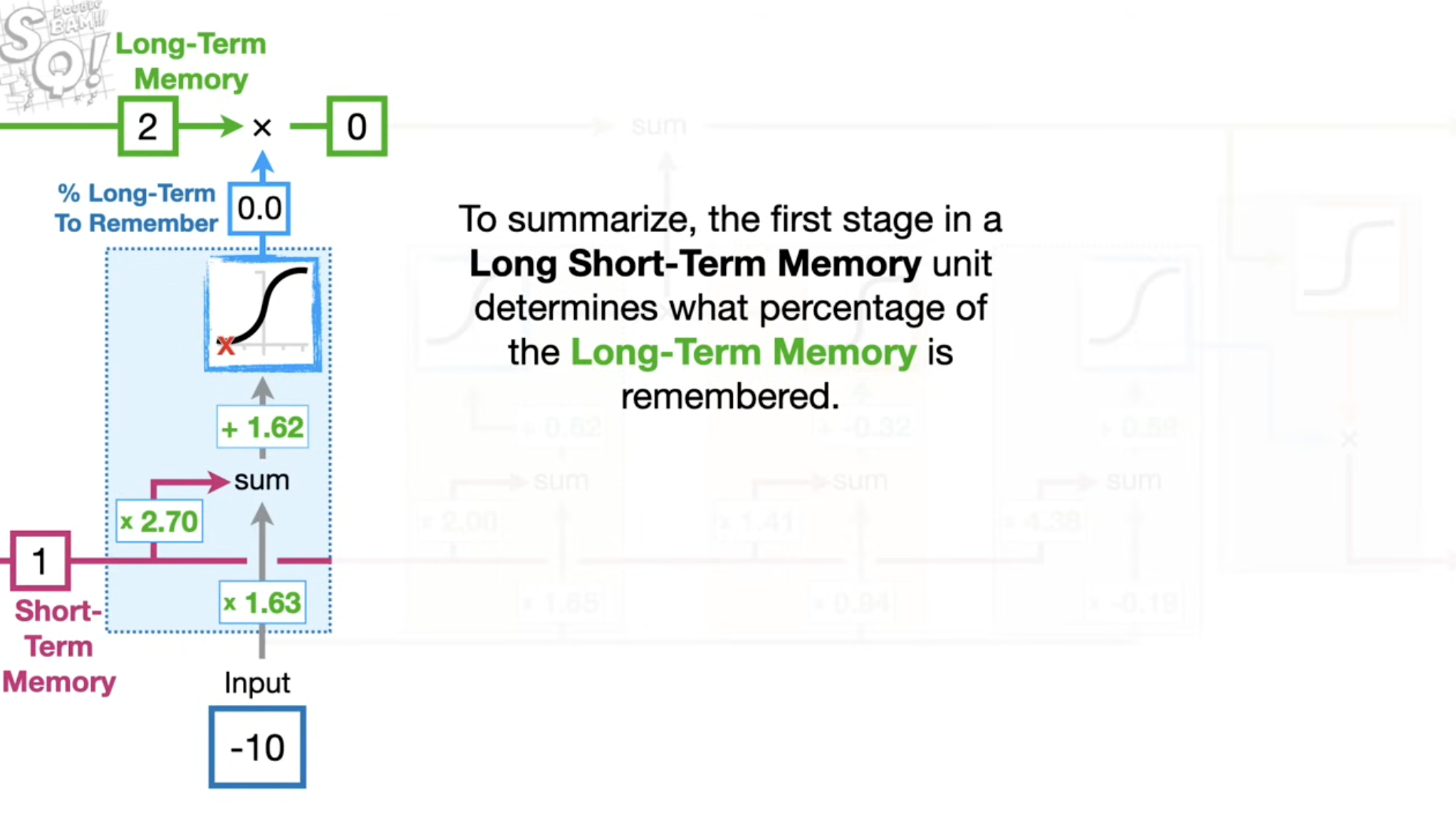
- 作用:决定要从上一个细胞状态 \(C_{t-1}\) 中丢弃哪些信息,或者说,在什么程度上保留过去长期记忆。
- 机制:它查看上一个时刻的隐藏状态 \(h_{t-1}\) 和当前时刻的输入 \(x_t\),然后两个向量 concat 后与参数矩阵做乘法得到新向量,sigmoid 激活使得 为 \(C_{t-1}\) 中的每个数字输出一个 0 到 1 之间的值。1 代表“完全保留”,0 代表“完全遗忘”。这个输出向量大小和状态向量 \(h_{t - 1}\) 是相同的。
-
公式:
$\(f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)\)$
这里有一个遗忘门的参数矩阵 \(W_f\),需要通过反向传播学习。
输入门 (Input Gate, \(i_t\))⚓︎
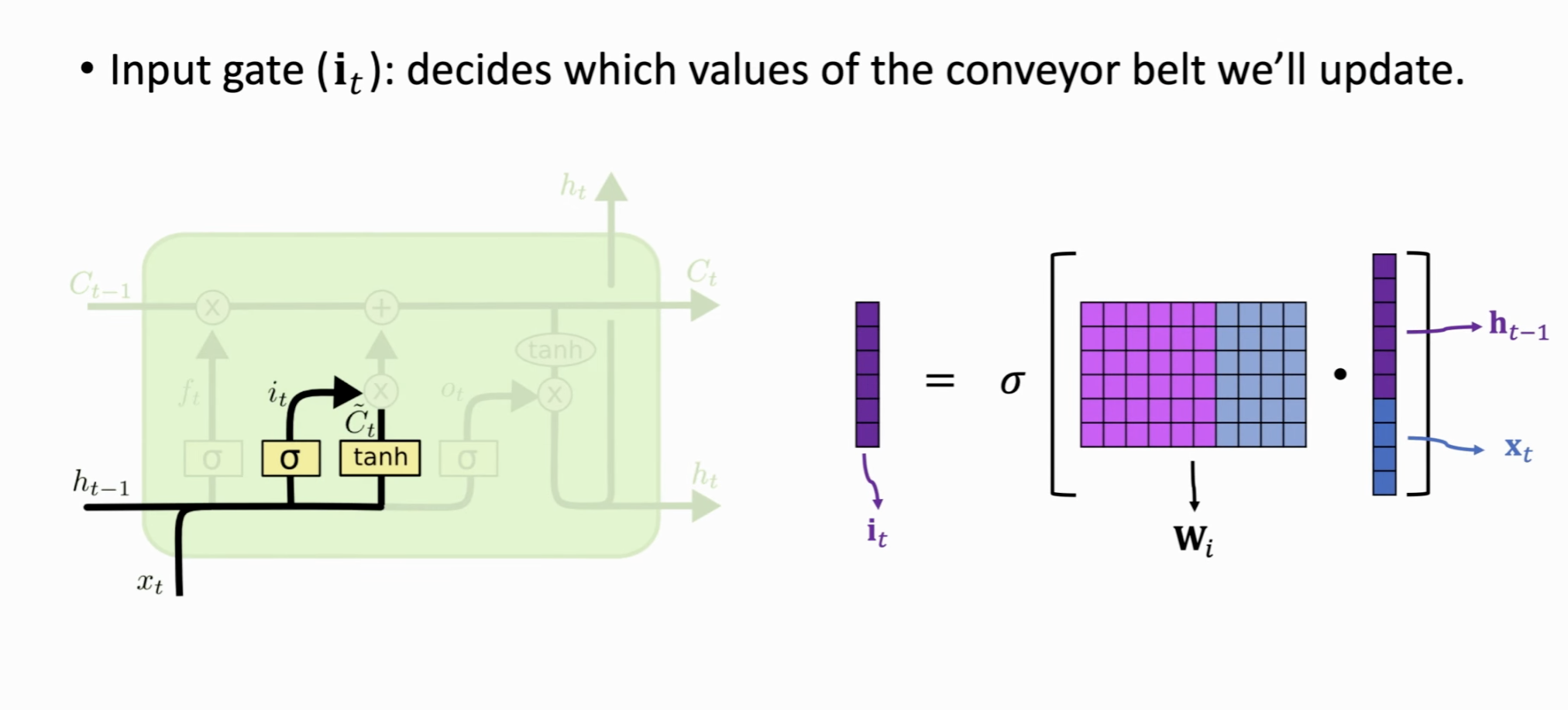
- 作用:决定要将哪些新的信息存入当前的细胞状态 \(C_t\) 中。这个过程分两步。
- 机制:
- 首先,输入门通过
sigmoid层决定我们要更新哪些值 (\(i_t\))。 - 然后,一个
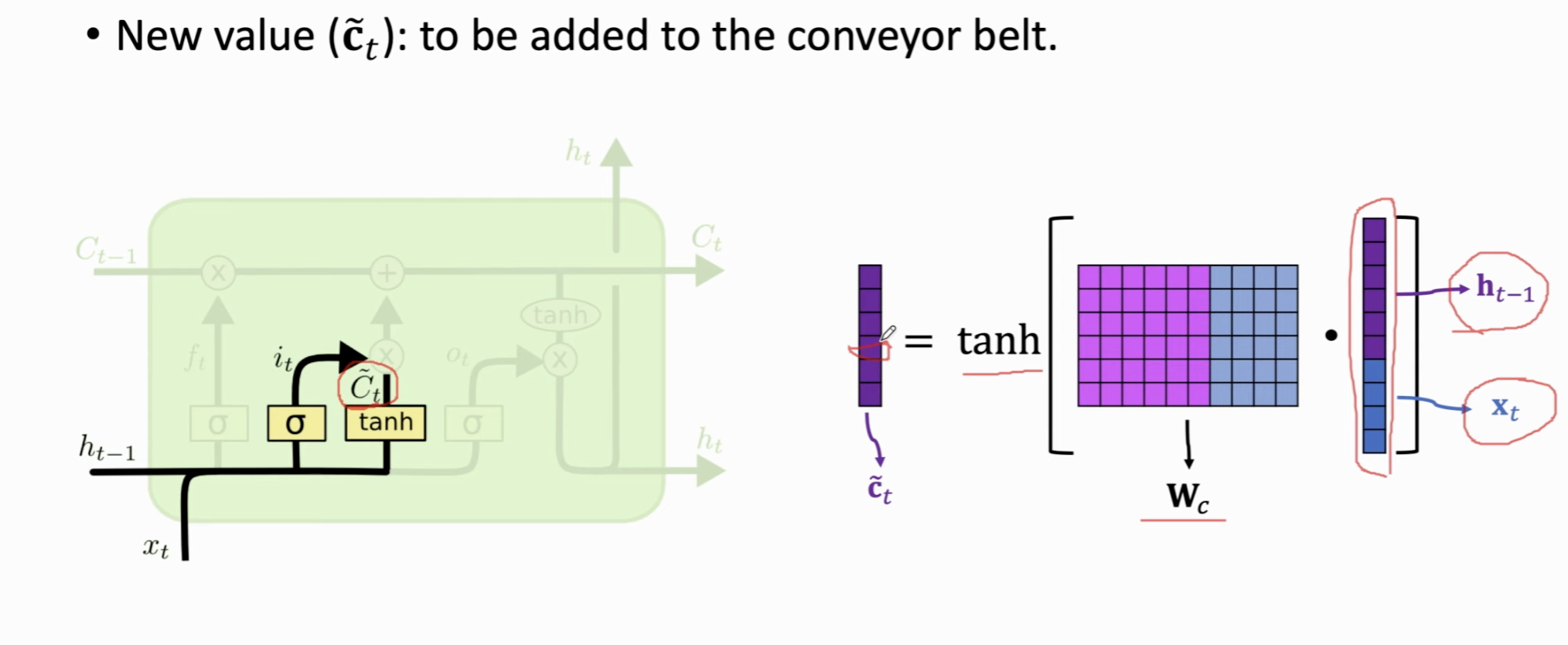
tanh层创建一个新的候选值向量 \(\tilde{C}_t\),这些值可能会被加入到细胞状态中。
- 首先,输入门通过
-
公式:
\[i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)\]\[\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)\]
第一步需要需要计算一个输入向量 \(i_t\),方式和遗忘门相同(用一个参数矩阵和concat后的状态向量+输入做矩阵乘法,然后sigmoid),这里需要学习一个参数矩阵 \(W_i\)。
第二部需要计算 New Value向量 \(\tilde{C}_t\),这里做法同上,区别在于激活函数是 \(\tanh\),这里的向量每个元素都在 \((-1, 1)\) 之间。注意了,这里我们又需要学习一个参数矩阵 \(W_c\)。
-
输入门的两部分功能:
-
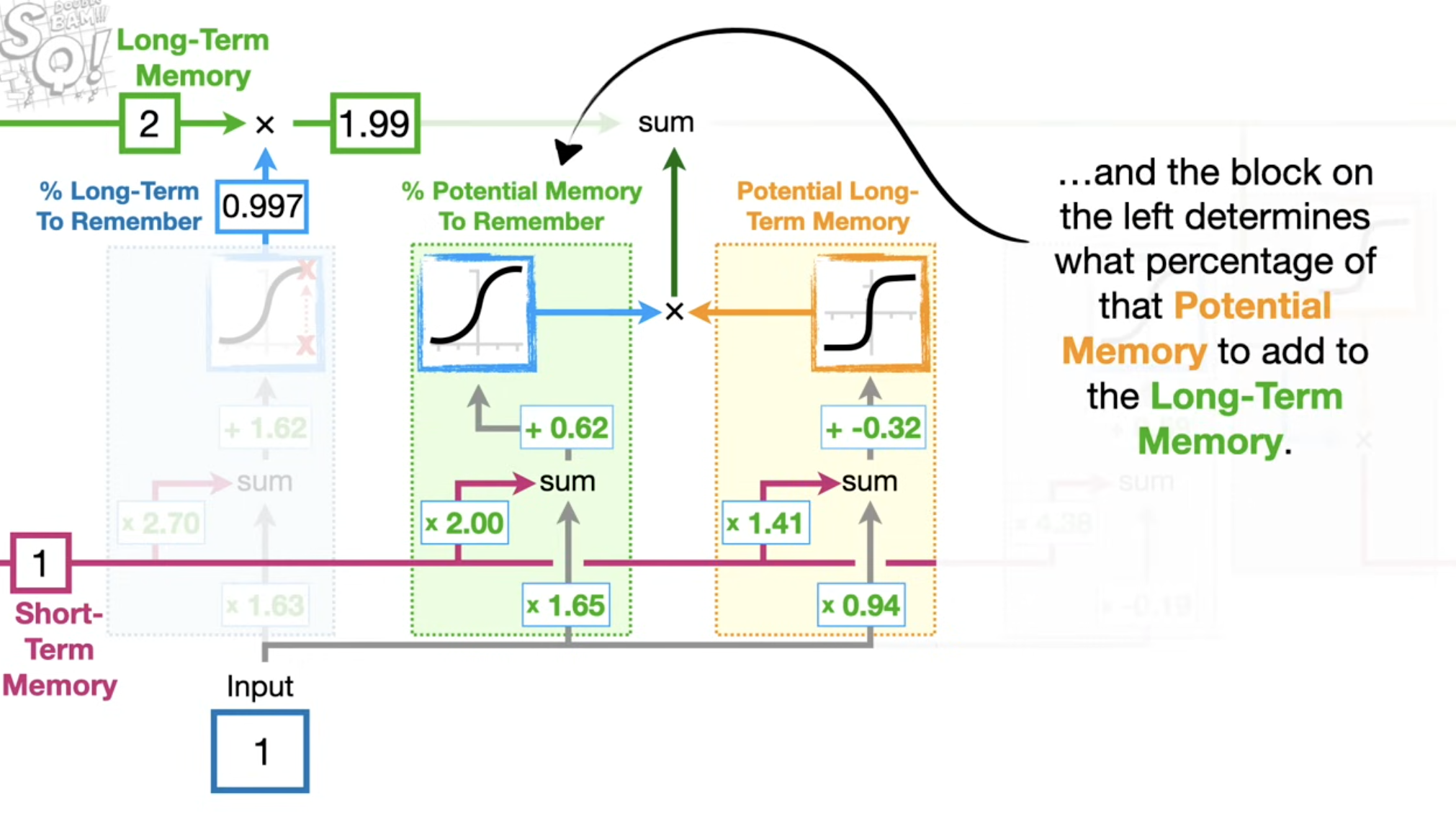
是记录当前有多少百分比的 Potential Long Term Memory 需要被记住。( At what percentage to saved)
- 决定Potential Long Term memory的数量是多少;通过对这两部分相乘,就能得到更新的Long Term Memory了。
可以发现,在输入门里,需要计算两部分内容,因此输入门是有两个参数矩阵需要调参数。这个 New Value门的作用就是决定Potential Long Term memory的数量是多少;
这里计算的一个New Value向量 \(\tilde{C}_t\),这里做法同上,区别在于激活函数是 \(\tanh\),这里的向量每个元素都在 \((-1, 1)\) 之间。注意了,这里我们需要学习一个参数矩阵 \(W_c\)。
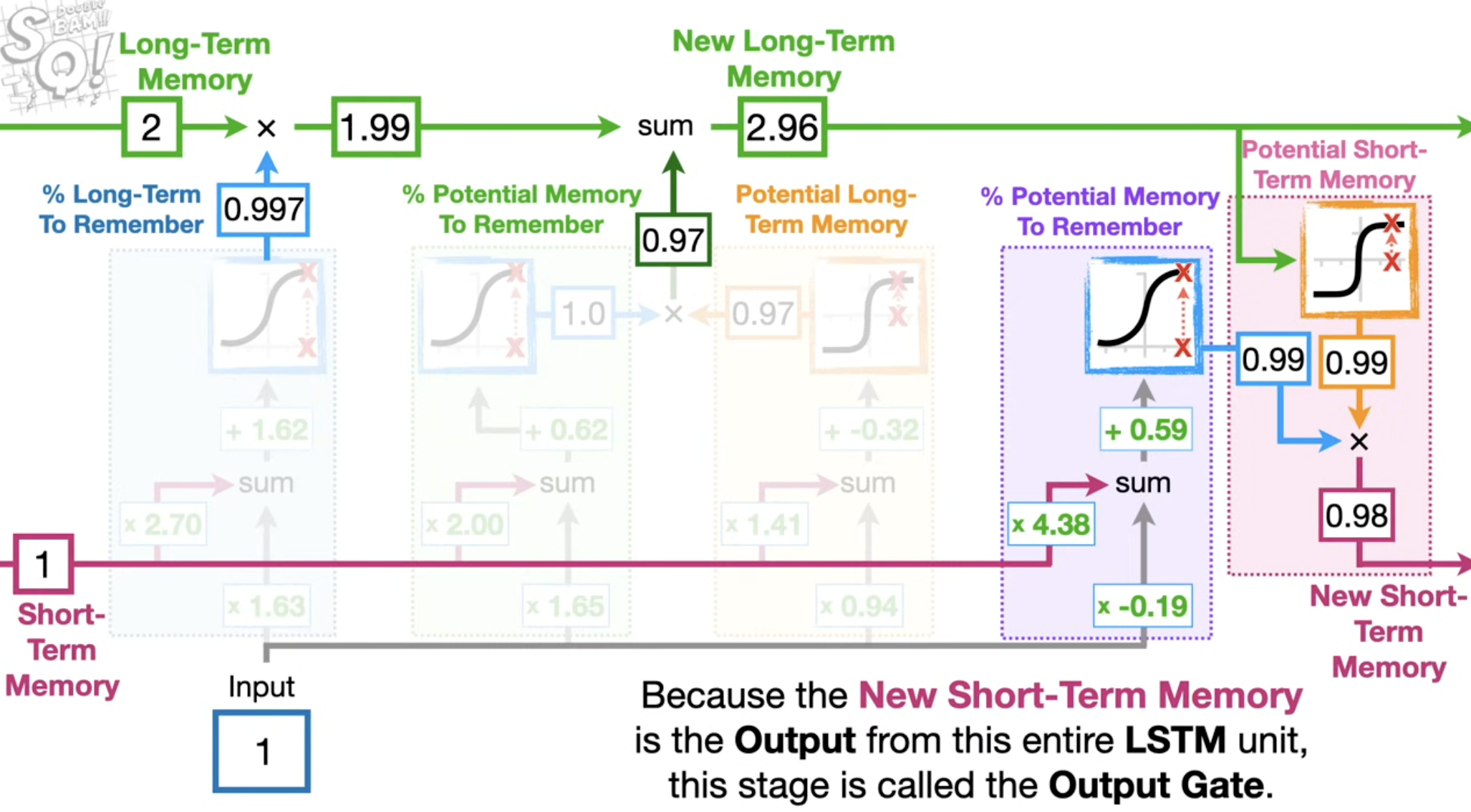
输出门 (Output Gate, \(o_t\))⚓︎
现在,我们有了前面几个环节的结果,是时候利用传送带了。
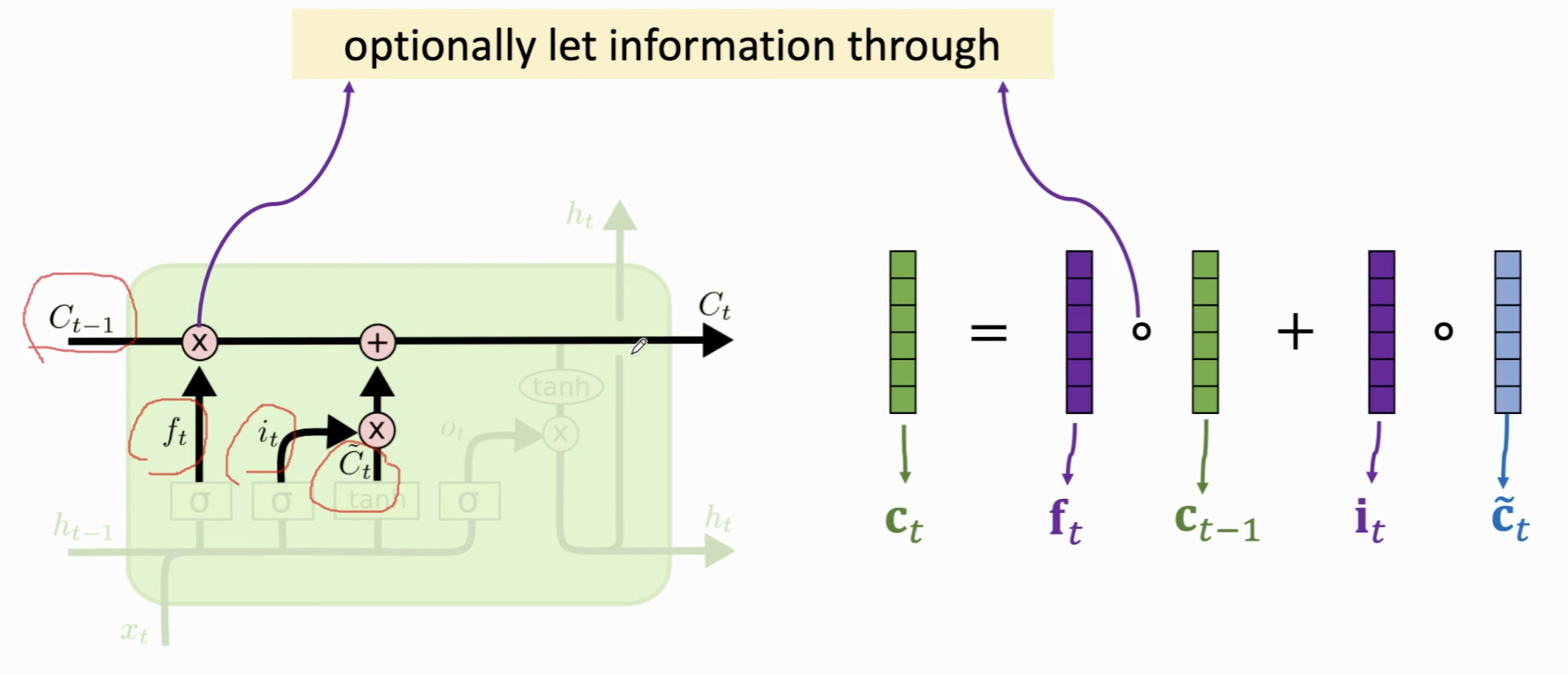
- 作用:决定要从当前的细胞状态 \(C_t\) 中输出什么信息。这个输出将作为当前时刻的隐藏状态 \(h_t\)。具体做法是我们利用遗忘门输出 \(f_t\),前一个状态向量 \(C_{t-1}\),输入门 \(i_t\) 以及Value向量 \(\tilde{C}_t\),更新传送带上的状态向量 \(C_t\)。
- 机制:
- 首先,输出门通过
sigmoid层决定我们要输出细胞状态的哪个部分 (\(o_t\))。 - 然后,我们将细胞状态 \(C_t\) 通过
tanh进行处理(将其值缩放到 -1 到 1 之间),并与 \(o_t\) 的输出相乘,得到最终的隐藏状态 \(h_t\)。
- 首先,输出门通过
-
公式:
$\(o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)\)$
由于我们先前保证了 \(C_t\) 和 \(f_t\) 以及 \(i_t\) 的尺寸相同,因此可以做 Element Piecewise Multiplication.
譬如 \(f_t c_{t-1}\) 的结果表示在当前状态选择性地遗忘掉先前状态的东西;\(i_t \tilde{c}_{t}\) 表示向传输带上添加某些新的信息。
也就是说,记录下“当前短期需要记住什么”,以及当前长期记住(忘记)了什么。
此时我们更新LSTM的输出。此时我们依然是把两部分做concat,然后学习一个参数矩阵 \(W_o\),经过sigmoid 后输出一个输出向量 \(o_t\),这个向量的大小,与传送带上涉及的若干向量都是相同的。
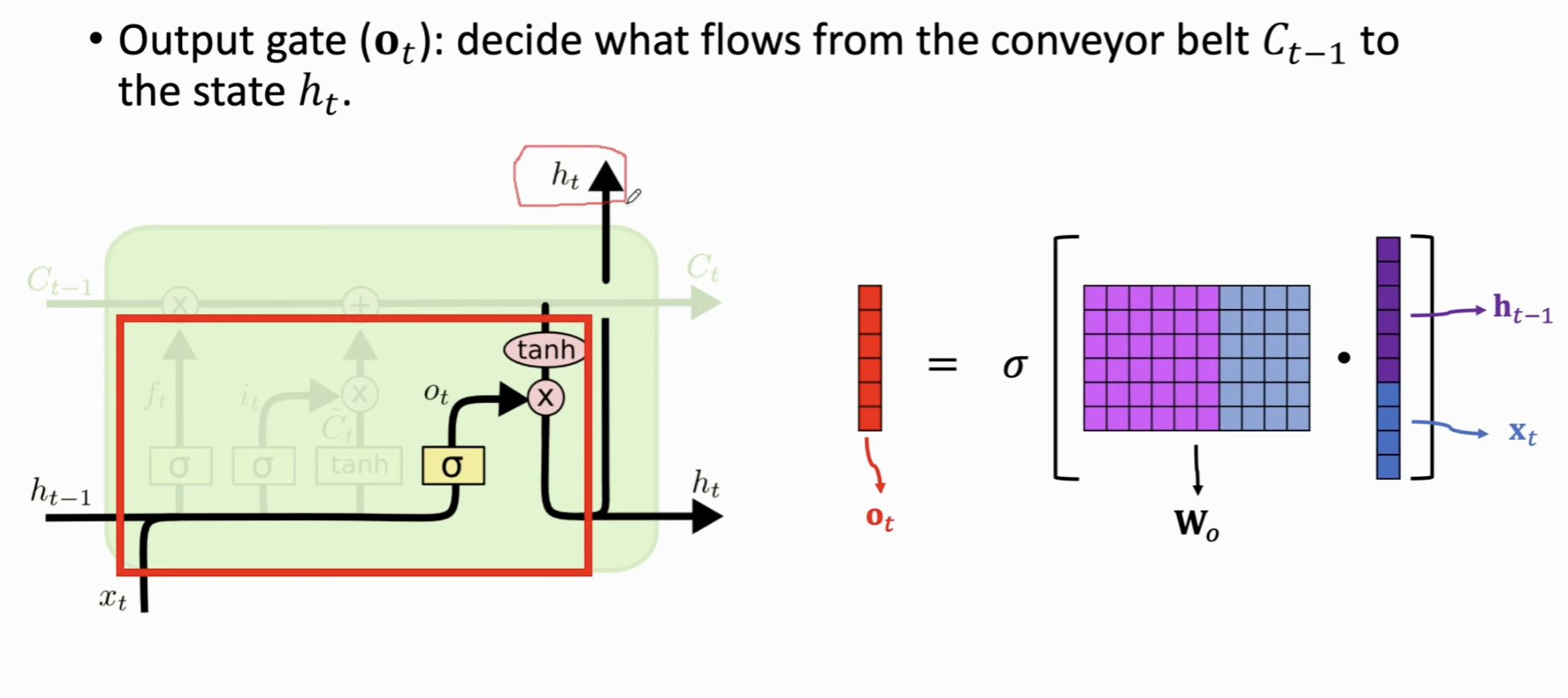
这个时候我们需要更新状态向量 \(h_t\),对于传送带上的信息 \(C_t\),做 \(\tanh\) 之后与输出向量做Element Piecewise Multiplication即可。这里的 \(h_t\) 既作为下一个状态的状态向量,又可以作为当前的输出结果,因此做2个copy。
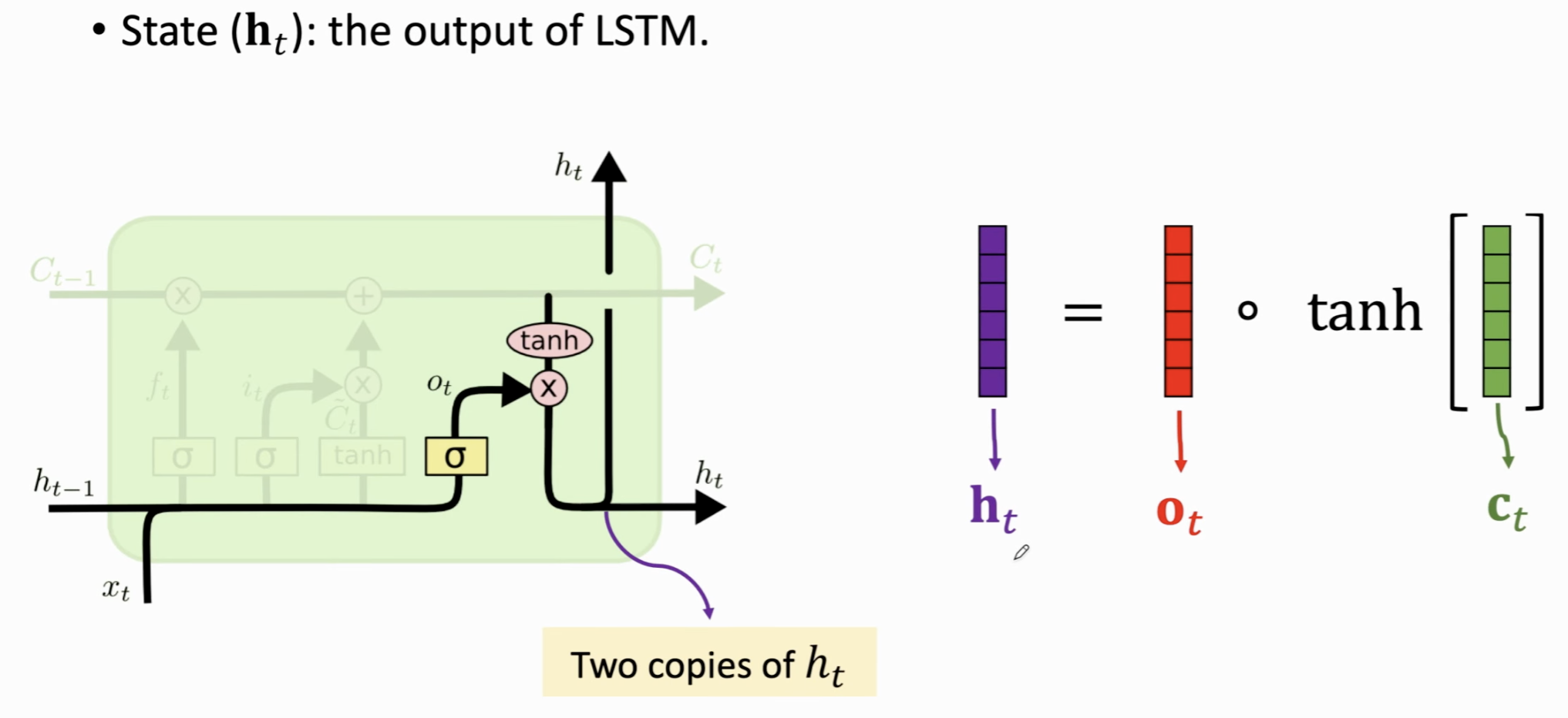
综上所述,这里的参数量由4个参数矩阵构成,分别属于:遗忘门、输入门、输出门。每个参数矩阵的参数规模 shape(h) \(\times\) [shape(h) + shape(x)],总参数规模 4 \(\times\) shape(h) \(\times\) [shape(h) + shape(x)]
总而言之,LSTM通过一个传送带,让过去信息容易传输到下一时刻,实现了比RNN更好的长期记忆。
LSTM中的四组核心权重⚓︎
一个标准的 LSTM 单元确实有三个门(遗忘门、输入门、输出门),但这三个门加上一个计算候选细胞状态的步骤,构成了四个独立的、需要学习参数的线性变换。这四个变换在结构上是平行的。
我们从头到尾重点关注参数矩阵:
前提设定:
* 输入向量: \(x_t\), 维度为 input_dim。
* 隐藏状态向量: \(h_{t-1}\) 和 \(h_t\), 维度为 hidden_dim。
* 细胞状态向量: \(C_{t-1}\) 和 \(C_t\), 维度也为 hidden_dim。
在每个时间步,LSTM 的计算都依赖于上一个时间步的隐藏状态 \(h_{t-1}\) 和当前时间步的输入 \(x_t\)。为了方便计算,通常会将这两者拼接 (Concatenate) 在一起,形成一个维度为 (hidden_dim + input_dim) 的新向量 \([h_{t-1}, x_t]\)。
现在,我们来看这四组权重是如何作用于这个拼接向量的:
- 遗忘门 (Forget Gate)
-
- 作用: 决定从旧的细胞状态 \(C_{t-1}\) 中遗忘多少信息。
- 计算: \(f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)\)
- 激活函数:
sigmoid。输出一个值在[0, 1]区间的向量,作为遗忘比例。0代表完全遗忘,1代表完全保留。 - 第一组权重: 权重矩阵
W_f和偏置向量b_f。
- 输入门 (Input Gate)
- 作用: 决定将多少新信息存入细胞状态。它本身并不创造新信息,而是作为新信息的“开关”。
* 计算: \(i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)\)
* 激活函数:
sigmoid。输出一个值在[0, 1]区间的向量,作为存入比例。 * 第二组权重: 权重矩阵W_i和偏置向量b_i。 - 候选细胞状态 (Candidate Cell State) / 新记忆内容
- 作用: 根据当前的输入和过去的隐藏状态,创造新的候选记忆 \(\tilde{C}_t\)。这部分内容将被输入门筛选后加入到细胞状态中。
* 计算: \(\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)\)
* 激活函数:
tanh。将新生成的记忆值压缩到[-1, 1]区间。使用tanh而不是sigmoid是因为它能产生正值和负值,允许模型对记忆进行增强或抑制,表达能力更强。 * 第三组权重: 权重矩阵W_C和偏置向量b_C。 - 输出门 (Output Gate)
-
- 作用: 基于更新后的细胞状态 \(C_t\),决定要输出什么信息作为新的隐藏状态 \(h_t\)。
- 计算: \(o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)\)
- 激活函数:
sigmoid。输出一个值在[0, 1]区间的向量,作为输出比例。 - 第四组权重: 权重矩阵
W_o和偏置向量b_o。
最终的隐藏状态 \(h_t\) 由输出门和经过 tanh 激活的细胞状态 \(C_t\) 共同决定:\(h_t = o_t * \tanh(C_t)\)。
权重矩阵的维度分析⚓︎
- 拼接后的输入向量 \([h_{t-1}, x_t]\) 的维度是
hidden_dim + input_dim。 - 所有四个线性变换(
f_t,i_t, \(\tilde{C}_t\),o_t)在计算后的输出维度都必须是hidden_dim。 - 根据矩阵乘法
output = W * input,我们可以推断出每个权重矩阵的维度。
对于 W_f, W_i, W_C, W_o 中的任何一个 W,它的维度都是:
[hidden_dim, hidden_dim + input_dim]
而每个偏置向量 b 的维度都是:
[hidden_dim]
举个例子:
假设你在做一个词性标注任务。
* 输入词向量的维度 input_dim = 300。
* 你设置的 LSTM 隐藏层维度 hidden_dim = 512。
那么:
1. 拼接向量 \([h_{t-1}, x_t]\) 的维度是 512 + 300 = 812。
2. 权重矩阵 W_f, W_i, W_C, W_o 的维度都是 [512, 812]。
3. 偏置向量 b_f, b_i, b_C, b_o 的维度都是 [512]。
4. 这个 LSTM 单元在一个时间步需要学习的总参数量就是:
$ 4 \times (\text{矩阵参数} + \text{偏置参数}) = 4 \times (512 \times 812 + 512) \approx 1.68 \text{M} \text{ parameters} $
这只是一个时间步的计算,这些参数是在所有时间步共享的。
实践中的优化:合并矩阵计算⚓︎
在 PyTorch、TensorFlow 等深度学习框架中,为了最大化计算效率(尤其是利用 GPU 的并行计算能力),通常不会进行四次独立的矩阵乘法。
框架会将这四个权重矩阵在内部合并成一个大的权重矩阵,进行一次矩阵乘法,然后将结果拆分成四部分。
- 合并后的权重矩阵
W_concat维度为[4 * hidden_dim, hidden_dim + input_dim]。 - 合并后的偏置向量
b_concat维度为[4 * hidden_dim]。
计算过程变为:
1. 进行一次大的矩阵乘法:result = W_concat * [h_{t-1}, x_t] + b_concat。
2. result 是一个维度为 [4 * hidden_dim] 的向量。
3. 将 result 切片成四份,分别送入各自的激活函数中。
为什么能缓解梯度消失?⚓︎
- RNN 的问题:标准 RNN 的隐藏状态更新是 \(h_t = \tanh(W_h h_{t-1} + W_x x_t + b)\)。在反向传播时,梯度会随着时间步连乘权重矩阵 \(W_h\)。 如果 \(W_h\) 的最大奇异值小于1,梯度会指数级衰减(梯度消失),导致无法学习长期依赖;如果大于1,梯度会指数级增长(梯度爆炸)。
- LSTM 的改进:LSTM 的核心改进是细胞状态 \(C_t\) 的加法更新机制 (\(C_t = f_t * C_{t-1} + i_t * \tilde{C}_t\))。反向传播时,梯度的传递路径上主要是按元素相乘(乘以门的输出值)和相加,而不是像RNN那样反复乘以同一个权重矩阵。这种结构创造了梯度的“高速公路”,使得梯度能够更平滑地在长序列中传递而不易消失。遗忘门 \(f_t\) 的存在,允许模型动态地控制梯度的流动,当 \(f_t\) 接近1时,梯度可以直接流过,当它接近0时,可以“切断”梯度流。
更精细的信息控制机制: * RNN 的问题:RNN 在每个时间步都会用新的输入和旧的隐藏状态完全重写其隐藏状态。它没有一个明确的机制来区分哪些旧信息应该保留,哪些新信息是重要的。 * LSTM 的改进:LSTM 引入的三个门(遗忘门、输入门、输出门)提供了一种对信息流的精细化控制。 * 遗忘门让模型学会忘记不再重要的历史信息。 * 输入门让模型学会有选择地记录当前输入中的关键信息。 * 输出门让模型学会根据当前任务需要,暴露记忆中的相关部分。 这种机制使得 LSTM 能够更智能地维护和使用其内部记忆。
总结⚓︎
可以按以下方式总结:
| 组件 | 目的 | 激活函数 | 权重/偏置 |
|---|---|---|---|
| 遗忘门 | 决定保留多少旧记忆 | sigmoid |
W_f, b_f |
| 输入门 | 决定接受多少新记忆 | sigmoid |
W_i, b_i |
| 候选记忆 | 生成可能的新记忆内容 | tanh |
W_C, b_C |
| 输出门 | 决定输出多少当前记忆 | sigmoid |
W_o, b_o |
这四组独立的、可学习的参数共同构成了 LSTM 的核心,使其能够灵活地控制信息流,从而有效地学习长期依赖关系。
LSTM 的复杂度分析⚓︎
这是一个多维度的问题,需要从时间复杂度(计算量)和空间复杂度(内存占用)两方面来回答。
核心结论先行:
假设序列长度为 T,输入维度为 d_in,隐藏层维度为 d_hid,批处理大小为 B。
- 时间复杂度: \(O(B \cdot T \cdot d_{hid} \cdot (d_{in} + d_{hid}))\)。在实际分析中,常简化为 \(O(T \cdot d_{hid}^2)\),因为通常 \(d_{hid}\) 远大于 \(d_{in}\),并且在讨论单个序列时忽略批处理大小
B。 - 空间复杂度:
- 参数: \(O(d_{hid} \cdot (d_{in} + d_{hid}))\)
- 中间变量/激活值: \(O(B \cdot T \cdot d_{hid})\)
下面我们来详细拆解这个结论。
时间复杂度主要由模型前向传播所需的浮点运算次数(FLOPs)决定。
单个时间步 -> 所有⚓︎
我们首先聚焦在一个时间步 \(t\) 内的计算量。如我们之前讨论的,LSTM 在一个时间步的核心计算是四个线性变换,它们共同作用于拼接向量 \([h_{t-1}, x_t]\)。
- 输入准备: 将上一个隐藏状态 \(h_{t-1}\)(维度
d_hid)和当前输入 \(x_t\)(维度d_in)拼接起来,得到一个维度为(d_in + d_hid)的向量。 -
核心计算:矩阵-向量乘法:
- 遗忘门: \(W_f \cdot [h_{t-1} \times x_t]\)
- 输入门: \(W_i \cdot [h_{t-1} \times x_t]\)
- 候选记忆: \(W_C \cdot [h_{t-1} \times x_t]\)
- 输出门: \(W_o \cdot [h_{t-1} \times x_t]\)
每个权重矩阵
W的维度都是[d_hid, d_in + d_hid]。一个m x n矩阵乘以一个n x 1向量的计算复杂度是 \(O(m \cdot n)\)。因此,这里单次矩阵-向量乘法的复杂度是 \(O(d_{hid} \cdot (d_{in} + d_{hid}))\)。
我们有四次这样的乘法,所以总复杂度是 \(4 \times O(d_{hid} \cdot (d_{in} + d_{hid}))\)。在 Big-O 表示法中,我们忽略常数
4。 -
其他计算: 剩下的计算,如偏置加法、逐元素乘法(Hadamard Product)和激活函数(
sigmoid,tanh),它们的复杂度都是 \(O(d_{hid})\)。 -
主导项: 显然,矩阵-向量乘法的复杂度 \(O(d_{hid} \cdot (d_{in} + d_{hid}))\) 远大于其他 \(O(d_{hid})\) 的计算。因此,一个时间步的计算复杂度由矩阵乘法主导,即 \(O(d_{hid} \cdot (d_{in} + d_{hid}))\)。
-
整个序列 (T个时间步): LSTM 的计算是顺序的,你必须计算完 \(h_{t-1}\) 才能计算 \(h_t\)。因此,你需要将单个时间步的计算重复
T次。-
总时间复杂度(单个序列)= \(T \times O(d_{hid} \cdot (d_{in} + d_{hid})) = O(T \cdot d_{hid} \cdot (d_{in} + d_{hid}))\)。
-
总时间复杂度(一批数据)= \(O(B \cdot T \cdot d_{hid} \cdot (d_{in} + d_{hid}))\)。
-
在讨论中,我们经常做一些简化假设:
- 隐藏层维度通常是主导因素,即 \(d_{hid} \gg d_{in}\)。在这种情况下,\((d_{in} + d_{hid}) \approx d_{hid}\)。
- 暂时不考虑批处理大小 B。
所以,时间复杂度常常被简化为:
\[O(T \cdot d_{hid} \cdot d_{hid}) = O(T \cdot d_{hid}^2)\]
这个简化的公式能让你快速地与其他模型进行比较。
空间复杂度 (Space Complexity)⚓︎
空间复杂度主要由需要存储在内存中的信息量决定,包括模型参数和中间激活值。
- 这是指模型本身(权重和偏置)所占用的空间。
- 我们有4组权重矩阵 (W) 和4组偏置 (b)。
- 每个
W的大小是[d_hid, d_in + d_hid],每个b的大小是d_hid。 - 总参数空间 = \(4 \times (d_{hid} \cdot (d_{in} + d_{hid}) + d_{hid}) = O(d_{hid} \cdot (d_{in} + d_{hid}))\)。
- 这个空间复杂度与序列长度 T 无关,因为参数是共享的。
激活值存储⚓︎
- 在训练过程中进行反向传播 (BPTT) 时,我们需要存储前向传播过程中计算出的所有中间变量(主要是每个时间步的隐藏状态 \(h_t\)、细胞状态 \(C_t\) 和各个门的输出)。
- 在每个时间步
t,我们需要存储的激活值大小约为 \(O(d_{hid})\)。 -
对于一个长度为
T的序列和大小为B的批次,需要存储的总激活值空间为:\[O(B \cdot T \cdot d_{hid})\] -
这个空间复杂度与序列长度 T 呈线性关系。当处理非常长的序列时,这部分内存占用可能会成为瓶颈。
延伸⚓︎
当面试官问你“LSTM的复杂度”时,你可以这样回答:
-
首先给出核心结论: “LSTM的时间复杂度与序列长度
T呈线性关系,与隐藏层维度的平方d_hid^2呈正比,约为 \(O(T \cdot d_{hid}^2)\)。空间复杂度则包括两部分:与序列长度无关的参数存储,以及与序列长度 T 线性相关的中间激活值存储。” -
解释时间复杂度的来源: “这主要是因为在每个时间步,LSTM 都需要进行若干次矩阵乘法,其复杂度由输入维度和隐藏层维度决定。由于计算是顺序进行的,所以总的计算量要乘以序列长度 T。”
-
点出与简单RNN的对比: “这个复杂度与简单RNN是同阶的。虽然LSTM内部有四个线性变换,看起来更复杂,但在Big-O表示法下,它们的复杂度级别是一样的,只是LSTM的实际计算常数因子更大(大约4倍)。”
-
与Transformer的对比: “这一点是LSTM/RNN与Transformer模型的关键区别。LSTM的复杂度与序列长度
T是线性关系,而标准Transformer的自注意力机制(Self-Attention)的复杂度与T是平方关系,即 \(O(T^2 \cdot d_{model})\)。这意味着当序列非常长时,Transformer的计算量会急剧增长,而LSTM则更具优势。但反过来,Transformer的计算可以在序列维度上完全并行,而LSTM必须按步顺序计算,这使得Transformer在硬件(如GPU)上的训练效率更高(对于中等长度的序列)。”
关于激活函数⚓︎
为什么有的地方用 sigmoid,有的地方用 tanh?
简单来说,这个设计选择是基于每个组件的功能目的以及激活函数本身的数学特性。
sigmoid的作用是“筛选”:它的输出范围是[0, 1],这可以被完美地解释为“通过的比例”或“开关的程度”。0代表完全关闭,1代表完全打开。因此,它被用在所有需要控制信息流的门(Gate)上。tanh的作用是“生成”:它的输出范围是[-1, 1],是零中心化的(zero-centered)。这让它可以描述“内容”或“状态”的变化,既可以表示正向增强(趋向1),也可以表示负向抑制(趋向-1)。因此,它被用在生成候选记忆和输出最终状态的地方。
下面我们通过一个表格来详细梳理每个位置的选择和原因。
LSTM激活函数的选择与作用⚓︎
| 位置 (Location) | 使用的激活函数 | 输出范围 | 目的与作用 |
|---|---|---|---|
| 遗忘门 (Forget Gate, \(f_t\)) | sigmoid |
\([0, 1]\) | 决定遗忘多少旧记忆。输出与旧细胞状态 \(C_{t-1}\) 逐元素相乘。值为 0 表示“完全忘记”,值为 1 表示“完全记住”。 |
| 输入门 (Input Gate, \(i_t\)) | sigmoid |
\([0, 1]\) | 决定接受多少新记忆。输出与候选记忆 \(\tilde{C}_t\) 逐元素相乘。值为 0 表示“完全不采纳新信息”,值为 1 表示“完全采纳新信息”。 |
| 输出门 (Output Gate, \(o_t\)) | sigmoid |
\([0, 1]\) | 决定输出细胞状态的多少部分。输出与经过tanh处理后的细胞状态 \(C_t\) 逐元素相乘,生成最终的隐藏状态 \(h_t\)。值为 0 表示“不输出任何信息”,值为 1 表示“完全输出”。 |
| 候选记忆生成 (\(\tilde{C}_t\)) | tanh |
\([-1, 1]\) | 生成新的、待添加的候选记忆内容。这部分是真正的新“信息”。使用tanh而不是sigmoid至关重要,因为它允许新信息对状态进行增加或减少。例如,一个接近 -1 的值可以削弱细胞状态中的某个维度。 |
| 细胞状态输出 (\(\tanh(C_t)\)) | tanh |
\([-1, 1]\) | 将细胞状态的值压缩到特定范围后,再输出。细胞状态 \(C_t\) 理论上没有范围限制,它通过不断的加法操作可能会变得很大或很小。在将其输出为隐藏状态 \(h_t\) 之前,用 tanh 将其值映射到 [-1, 1],可以防止数值爆炸并保持输出的稳定性。 |
为什么不能混用?⚓︎
1. 如果把门(Gates)的激活函数从 sigmoid 换成 tanh?
tanh的输出范围是[-1, 1]。如果门的输出是负数,这在物理上很难解释。例如,遗忘门的输出是-0.5,难道是“反向遗忘”或者“增强一个负向的记忆”吗?这会使得门的“开关”或“比例”作用失效,模型将很难学习到稳定的控制信息流的策略。虽然理论上模型可以通过学习将权重调整到只使用tanh函数的[0, 1]区间,但这无疑增加了优化的难度和不稳定性。
2. 如果把候选记忆生成 \(\tilde{C}_t\) 的激活函数从 tanh 换成 sigmoid?
sigmoid的输出范围是[0, 1]。这意味着候选记忆 \(\tilde{C}_t\) 的值将永远是正数。- 回顾细胞状态的更新公式:\(C_t = f_t * C_{t-1} + i_t * \tilde{C}_t\)。
- 如果 \(\tilde{C}_t\) 总是正数,那么 LSTM 将只能向细胞状态中增加信息,或者保持不变,但永远无法减少或削弱某个维度的值(除非通过遗忘门完全忘记)。
- 这极大地限制了模型的表达能力。例如,当模型读到一个否定词(如 "not good"),它需要有能力将代表 "good" 的正面情绪向量减弱或反转。如果只能增加正值,这个操作将变得非常困难。而
tanh的[-1, 1]范围完美地解决了这个问题。
总结⚓︎
"LSTM中sigmoid和tanh的选用是基于它们各自的数学特性和在模型中扮演的功能角色精心设计的。
sigmoid函数被用在所有的门(遗忘门、输入门、输出门)上。因为它的输出范围是[0, 1],可以完美地模拟一个'门',用来控制信息的通过比例——0代表完全阻断,1代表完全通过。tanh函数则被用在生成候选记忆和输出最终隐藏状态这两个环节。它的输出范围是[-1, 1],并且是零中心化的。这使得它非常适合用来编码和生成'信息内容'本身,因为它允许模型为状态添加正向或负向的更新,表达力更强。例如,它可以让模型学会在看到否定词时,向细胞状态中添加一个负值,从而削弱或反转之前积累的某个特征。
总而言之,sigmoid 负责当‘控制器’(Gate Controller),而 tanh 负责当‘内容生产者’(Content Producer)。这种设计上的分工合作,是LSTM能够有效管理记忆和处理长期依赖的关键所在。"