循环神经网络⚓︎
约 1640 个字 3 张图片 预计阅读时间 5 分钟 总阅读量 次
序列数据⚓︎
实际中许多数据是有时序结构的,也就是序列数据。比如语言、音乐、文本、电影的评分评价(贺岁片、奖项)等随着时间变化而变化。
在时间 \(t\) 观察到 \(x_t\),那么得到 \(T\) 个不独立的随机变量 \((x_1, x_2, ..., x_t) \sim p (\mathbf{x})\)
用条件概率展开联合概率: \(p(a, b) = p(a) p(b | a) = p(b) p(a|b)\)
也就是 \(p(\mathbf{x} ) = p(x_1) \cdot p(x_2 | x_1) \cdot p(x_3 | x_2, x_1) ... \cdot p(x_T | x_{T - 1}, x_{T - 2} ... x_1)\)
我要想知道最后一刻发生什么,需要把前面所有发生的概率都求出来。
也可以反过来写:
\(p(\mathbf{x}) = p(x_T) \cdot p(x_{T - 1} | x_T) \cdot p(x_{T - 2} | x_{T - 1}, x_{T} ) ...\)
对条件概率建模:
\(p(x_t | x_1, ... x_{t - 1}) = p(x_t | f(x_1, ..., x_{t - 1}))\)
和图片分类不同,我们现在是给定前 \(t - 1\) 个数据来预测第 \(t\) 个数据。也就是对见过的数据建模,也就是自回归模型。
问题就变成了,如何计算这个 \(f(x_1,. .., x_{t - 1})\)。
马尔可夫假设⚓︎
假设当前数据只和 \(\tau\) 个过去数据点相关,不用看过去所有的数据。
\(p (x_t | x_1, ... x_{t - 1}) = p(x_t | x_{t - \tau}, ..., x_{t - 1}) = p (x_t | f(x_{t - \tau} ..., x_{t - 1}))\)
比如在过去数据上训练一个 MLP 模型:如果 \(x\) 是个标量,那么每次给定一个 \(\tau\) 长的特征,输出一个标量即可。
潜变量模型 (Latent variable)⚓︎
\(p(\mathbf{x}) = p(x_1 ) \cdot p(x_2 | x_1) \cdot p(x_3 | x_1, x_2) ... p(x_T | x_1, ... x_{T - 1})\)
引入一个变量 \(h_t\) 来概括过去信息 \(h_t = f(x_1, ..., x_{t - 1})\)
先前的是把这个信息建模成一个模型,现在是变成一个变量了。所以:
\(x_t = p(x_t | h_t)\)
这种方法下我们可以不断更新 \(h\) 的值:一共两个模型:
- 怎么根据 \(x_{t - 1} , h_{t - 1}\) 来计算 \(h_t\)
- 怎么根据 \(x_{t - 1}\) 与 \(h_{t}\) 预测 \(x_{t}\) 也就是 \(\hat{x}_t\)
文本预处理⚓︎
把文本作为一个序列数据的方法,从而能够进行训练。
- 把文本拆分成单词或者字符的标记。
- 构建一个字典(词汇表),用来把字符串类型的标记映射到从 0 开始的数字索引上。
- 把整个文本映射到一个用数字表示的列表中。
语言模型⚓︎
语言模型的目标是给定文本序列 \(x_1, .., x_T\),估计其联合概率: \(p(x_1, ..., x_T)\)。
应用:预训练模型、文本生成、判断序列哪个常见(语音识别的优化)。
使用计数来建模(统计学方法)⚓︎
假设序列长度为 2,我们用这个序列出现次数来预测概率:
\(p(x, x^{'}) = p(x) p(x|x^{'}) = \dfrac{n(x)}{n} \dfrac{n(x, x^{'})}{n(x)}\)
这里 \(n\) 是总词数,\(n (x, x^{'})\) 表示连续单词对的出现次数。
N 元语法(N-gram)
序列很长的时候,文本量不够大,需要用马尔可夫假设:
一元:\(p(x_1, x_2, x_3, x_4) = p(x_1) p(x_2) p(x_3) p(x_4)\)
二元:\(p(x_1, x_2, x_3, x_4) = p(x_1) p(x_2|x_1) p(x_3 | x_2) p(x_4 | x_3)\)
以此类推。也就是说,这个文本序列出现概率,每个词的出现概率只依赖前面那 \(n - 1\) 个字符的概率。
这种方式可以处理比较长的序列了。
这有个问题。需要存所有长度为 n 的序列的情况存下来。比如一个文本数据,你需要存所有长度为 3 的文本出现次数等。
这里有一个优化方向是做低频词过滤。
算法实现时候有个关于采样方法的细节。假设文本已经Token已经表示成数字下标(corpus),现在需要把一个Token序列变成一个Mini-Batch,在随机采样中,每个样本都是在原始的长序列上任意捕获的子序列。比如长度为 \(T\),但是开始时候的偏移量不同,这样不会重复取到一个相同的 \(T\) 序列。
循环神经网络⚓︎
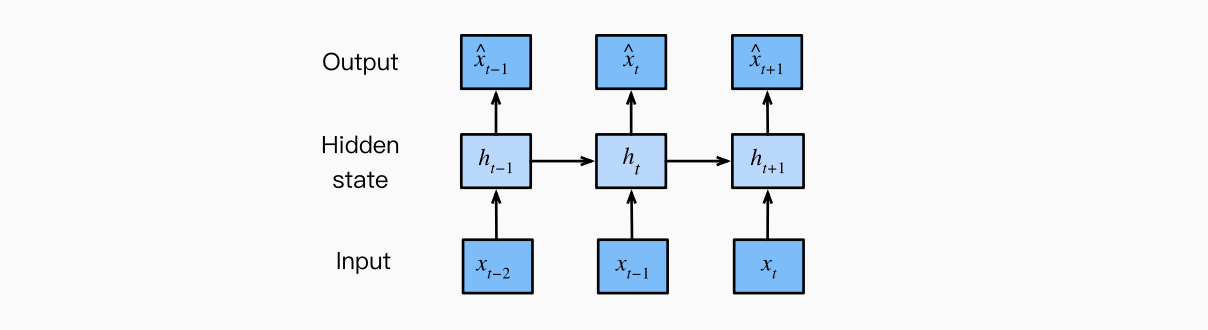
从潜变量自回归模型开始!
使用潜变量 \(h_t\) 总结过去的信息。
\(p(h_t | h_{t - 1}, x_{t - 1})\)
\(p(x_t | h_t, x_{t - 1})\)
更新隐藏层:\(\mathbf{h}_t = \phi (\mathbf{W}_{hh} \mathbf{h}_{t - 1} + \mathbf{W}_{hx} \mathbf{h}_{t - 1} + \mathbf{b}_h)\)
如果去掉 \(\mathbf{W}_{hh} \mathbf{h}_{t - 1}\),就退化成一个 MLP。
-
这里的 \(\mathbf{W}_{hx}\) 是隐藏层的权重(weight),但是是作用在 \(\mathbf{x}_{t - 1}\) 上的,重要的是它还和前一刻的 \(h\) 相关。
-
为了表示和前一刻的隐藏层相关,所以需要有 \(\mathbf{W}_{hh} \mathbf{h}_{t - 1}\),也就是其前一个时刻的隐藏状态对应的权重。
- 简单理解就是 相比 MLP 多加了一项,这样可以和前一个时刻的 \(h\) 发生关系。
输出: \(\mathbf{o}_t = \phi (\mathbf{W}_{ho} \mathbf{h}_t + \mathbf{b}_o)\)
在 \(t\) 时刻的输出,利用 \(h_t\) 即可完成。
在 0 时刻的输入,是不需要有输出的,而是会更新隐变量,预测 1 时刻的输出(此时是没有1时刻的观察的!)
以此类推。在 \(t\) 时刻的输出 \(o_t\) 来自于 \(h_t\), \(h_t\) 会因为观察到的 \(x_{t - 1}\) 更新,所以会受到 \(x_{t - 1}\) 和 \(h_{t - 1}\) 的影响。更新完后,我们用 \(h_t\) 进行预测。
用什么方法衡量语言模型的好坏:平均交叉熵⚓︎
\[\pi = \dfrac{1}{n} \sum^n_{t = 1} - \log p(x_t | x_{t - 1}, ... )\]
把语言模型视为分类模型,实际上就是判断下一个词的出现概率(字 m 在字典中的出现概率)。比如假如文本长度 \(n\) ,那么就是要做 \(n\) 次预测。
实际做的时候使用困惑度 \(\exp(\pi)\) 来衡量。是平均每次可能选项。
Trick: 梯度剪裁⚓︎
迭代中计算 T 这个时间步的梯度,反向传播过程中有 \(O(T)\) 的矩阵乘法链条,导致数值不稳定。梯度剪裁可以有效防止梯度爆炸。如果梯度的长度超过 \(\theta\),那么拖影回 \(\theta\)。
\(g \leftarrow \min (1, \dfrac{\theta}{||g ||})g\)
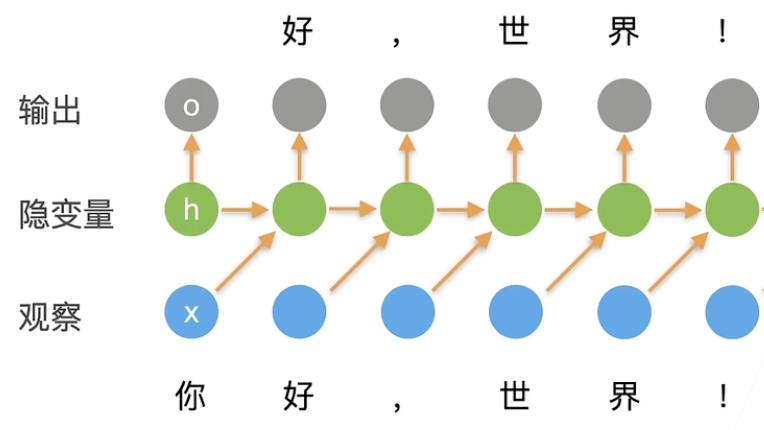
RNN 的一些应用⚓︎
如图所示。