跳转至

实用机器学习 by 李沐⚓︎

约 3700 个字 34 行代码 10 张图片 预计阅读时间 13 分钟

说在前面

本部分是一个笨笨的优化er第一次试着做机器学习相关的内容总结和代码分享。

目前我希望做的是基于具体案例和代码的机器学习快速入门。这是一门工程学科。所以目前打算尽可能简略地榨干相关知识，然后以代码（各种来源的都有）训练基本技能。

以下是本部分的参考内容：

网站：https://c.d2l.ai/stanford-cs329p/；李沐的实用机器学习

中文版视频链接：BiliBili Links;

我的代码库：Github Repo；

1.1 Introduction⚓︎

机器学习的流程。

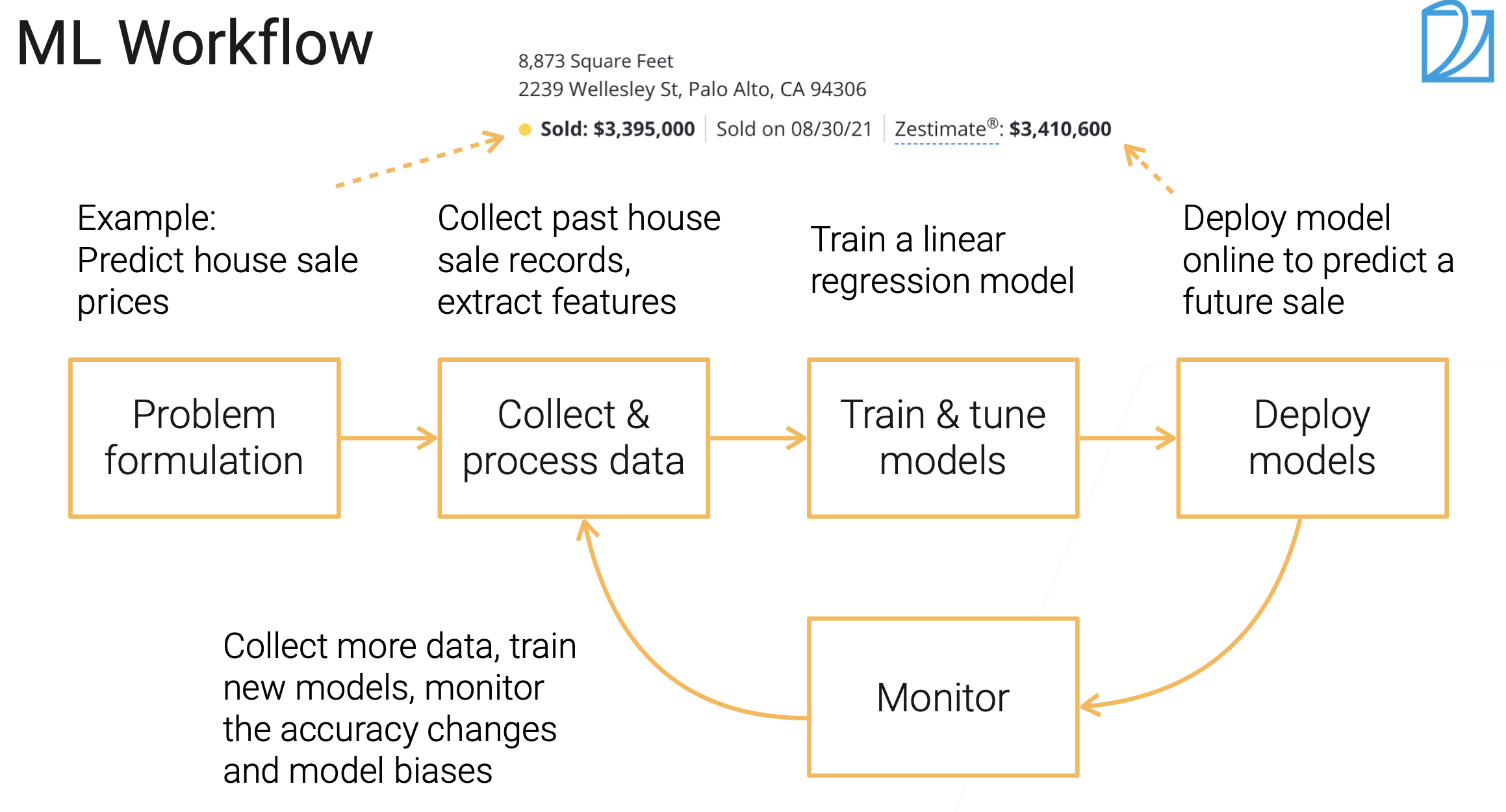
首先是确定问题。注意，有些任务对机器，其实学习起来很难，但是对人类很简单：叠衣服、自动驾驶；但是有的任务，对人类可能很难（很耗时），但是对机器可能很简单，比如，翻译成一个自己不会的语言。

其次是收集和处理数据。

接着去训练模型、调参等；最后可以部署到线上，可真的预测一些东西。部署了之后需要关注模型的性能、预测精度、延迟等。同样部署后会得到新的数据，然后和原先数据融合，再进行训练等。

预测房价的案例

本质上是一个“回归”的问题。

开始训练模型的时候，一开始肯定是从简单的模型开始（Like 线性回归）。用来测试数据的好坏。

Challege

注意，需要关注那些能够让公司利润最大化的那些问题。

其次，数据饥饿：Data Hungry.

算法公平性的问题：算法本身不会特别偏向谁，但是数据会。因为数据可能在一些有代表性的人群里表现很好，但是对其他人未必。

不同的人在机器学习项目中扮演的角色。

  1. Domain Expert： 有商业见解；知道重要数据、如何找重要的数据等；
  2. Data Scientist: 全栈的。数据挖掘、部署等；
  3. ML Expert: 对模型做定制化；
  4. 软件开发工程师；打通Pipeline，模型训练和跑通pipeline，包括产品组建、数据流等；实际上我们会训练很多模型；

2.2 Data Cleaning⚓︎

Types of data error
1.Outliers: data values that deviate from the distribution of values in the column 2. Rule violations: violate integrity constraints such as "Not Null" and "Must be unique" 3. Pattern violations: violate syntactic and semantic constraints such as alignment, formatting, misspelling

3.1 ML Model Overview⚓︎

机器学习算法的分类

监督学习(supervised learning)✨

基于有标记的数据进行训练，并进行预测；

self-supervised learning: 标记是通过数据本身生成的。e.g. Bert

半监督学习(semi-supervised learning)
有一部分数据有标号，有一部分数据没有标号。基于这些数据进行训练，对标号进行预测等；
无监督学习(unsupervised learning)
基于无标记的数据进行训练，并进行预测；GAN，cluster等；
强化学习(Reinforcement Learning)
基于环境进行训练，通过不断与环境交互，得到反馈reward，学习到最优策略；

监督学习的组成

模型(Model)
根据输入作出输出预测；output predicts from input
损失函数(Loss Function)
衡量预测值与真实值之间的差距，用于优化模型；
目标(objective)
Any function to optimize during training. e.g. 使得在训练数据上的损失函数总和最小；
优化(optimization)
把模型中可以学习的参数找到对应的值，也就是找到最优模型参数

监督学习的分类

  • 决策树(Decision Tree)
  • 线性方法(Linear Regression)
  • 核函数
  • 神经网络

4.3 Model Validation⚓︎

Generalization error.
Error on a test dataset, which can only be used once.

正因为泛化误差是在测试集上使用，用过一次就不能再用了（因为模型也可以学习这些误差），对数据而言是一种浪费，所以需要用到 Validation dataset（验证集）.

Validation dataset
  1. often part of training dataset;
  2. when we use the term 'test', mostly we mean 'validation'

生成Validation dataset的方法

  1. Split your data into 'train' and 'validation' datasets.(Often randomly select \(n\%\) samples)
  2. Use the error on the valid dataset to approximate the generalization error.

不是每个案例中的数据集都是可以随机分的。

  1. 时序信息，比如房价、股票等，不能随机分，因为会丢失时序信息；
  2. Photos of same person. 因为同一个人的脸可能同时出现在train / valid 数据集中。
  3. 数据不平衡：Sample from minor group. 需要先制作成平衡的数据集。

K-fold validation

把数据分成K份，每次取第 i 个作为验证集，剩下的 K-1个作为训练集。

优点：

  1. 当数据量不充分的时候很有用；
  2. 能够反映 \(K\) 个验证集误差的平均值。

通常， K 取 5 或者 10.

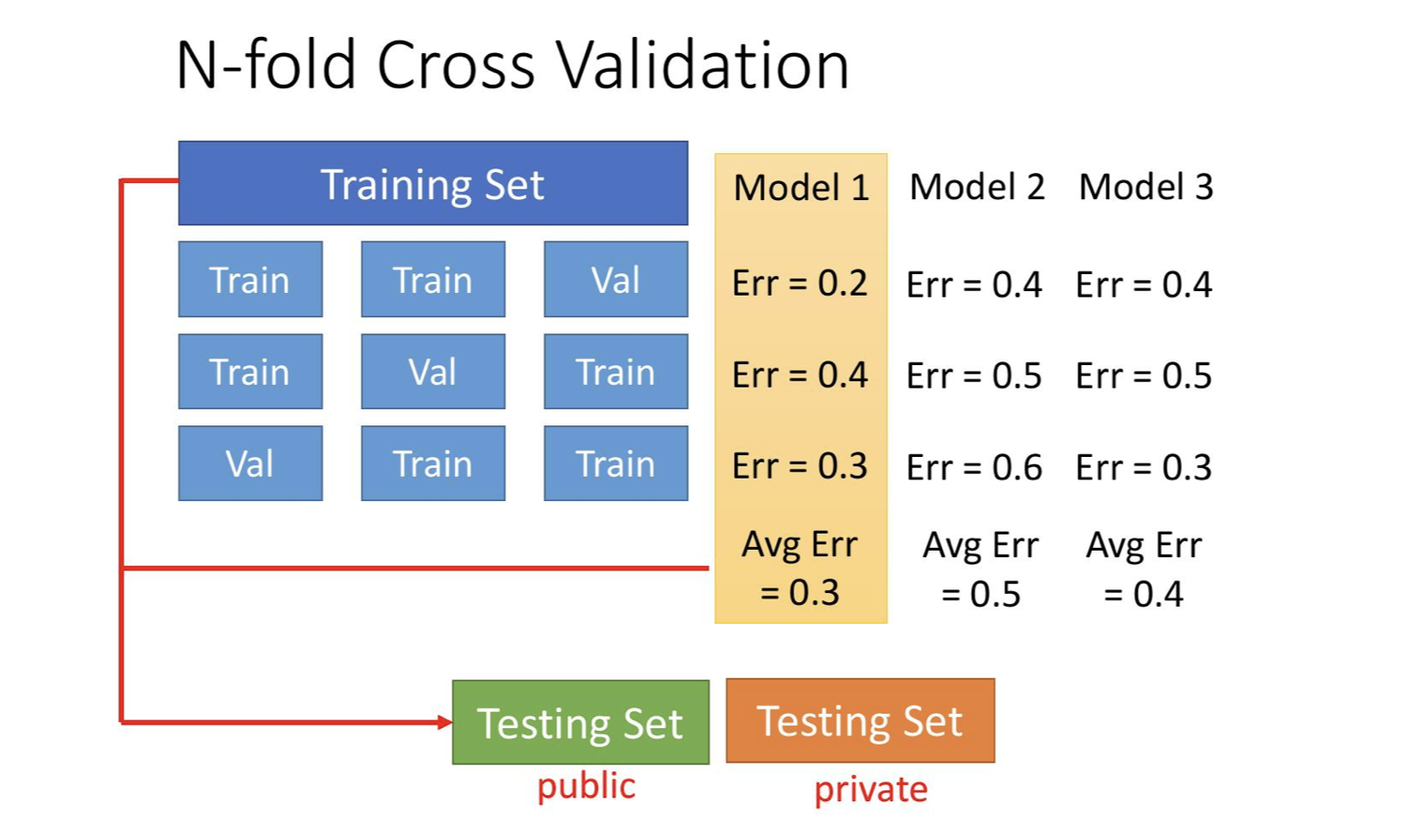
常见误区： 90% good results in ML are due to bugs.

原因很多，其中之一是，数据集选取可能出现重复（同时在训练集和验证集中出现）。因此尤其是在融合多个数据时候，要甄别冗余数据。

5.1 Bias, Variance⚓︎

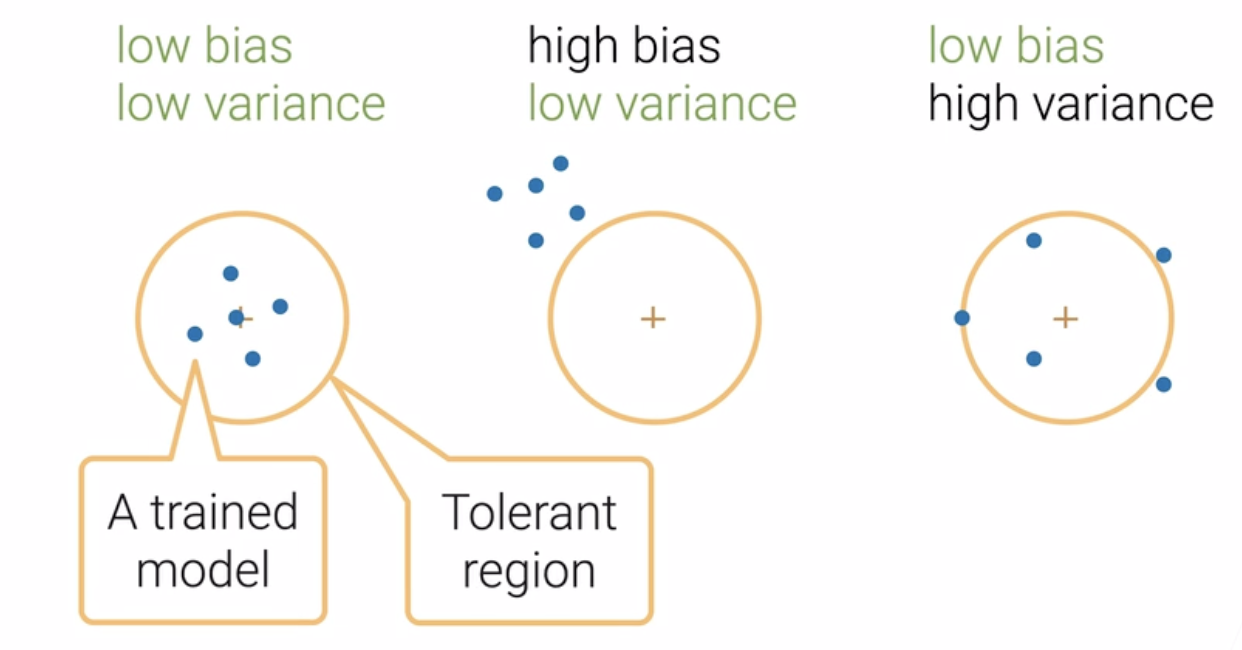
低偏差和低方差是我们所追求的。

Bias-Variance Decomposition⚓︎

Sample data \(D = \{ (x_1, y_1), (x_2, y_2),..., (x_n, y_n) \}\) from \(y = f(x) + \epsilon\).

Learn \(\hat{f}\) by min MSE. which is:

\(E_D [ (y - \hat{f}(x))^2 ] = E_D [ (f(x) + \epsilon - \hat{f}(x))^2 ]\)

$ = E [ (f - E[\hat{f}] + \epsilon - (\hat{f} - E[\hat{f}] )^2]$

$ = (f - E(\hat{f}))^2 + E[\epsilon^2] + E[(\hat{f} - E[\hat{f}])^2]$

这里的第一项，就是偏差的平方；第二项，表示噪音的方差；第三项，表示方差。

  1. \(E(f) = f\)

  2. \(E(\epsilon) = 0\)

  3. \(Var (\epsilon) = \sigma^2\)

  4. \(\epsilon\) is independent of \(\hat{f}\)

Bias-Variance Tradeoff⚓︎

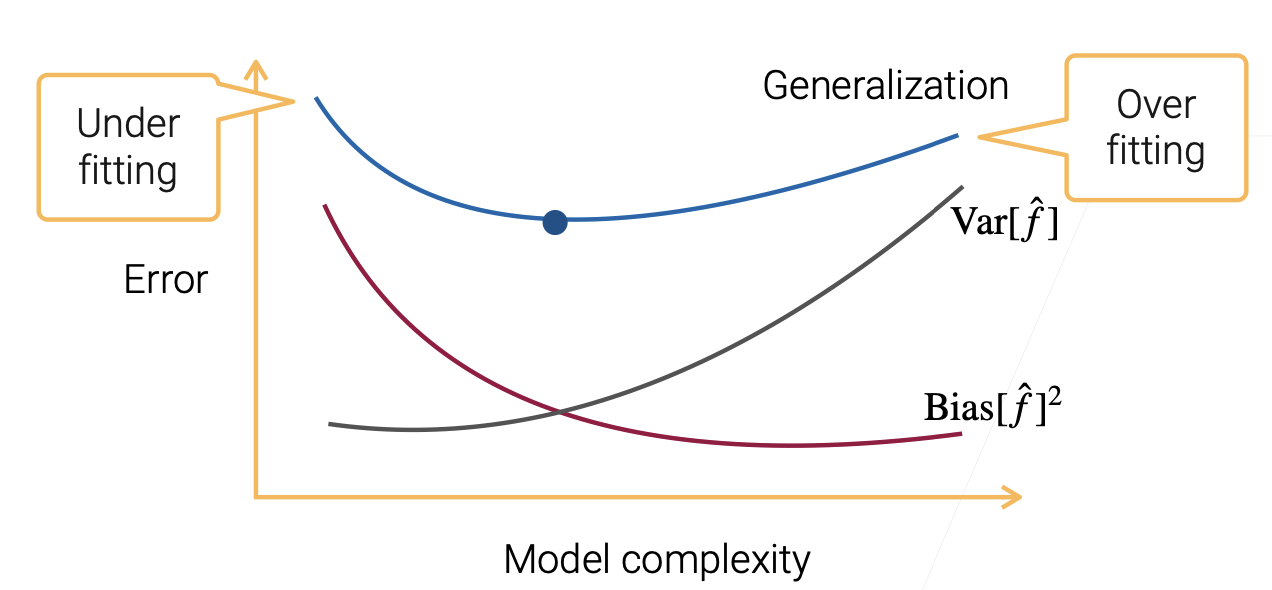
一开始，模型简单，偏差和真实的值之间是比较远的；后来模型复杂了，偏差会逐渐减小；但是随着模型复杂度增加，我能拟合的东西就越来越大（假定数据大小不变），模型比数据复杂太多，导致模型过度关注其中的一些噪音（过拟合），导致方差逐渐增加。

Our mission:⚓︎

Reduce Bias & Variance & Noise.

Reduce Bias
  1. More Complex Model;
  2. Boosting / Stacking
Reduce Variance
  1. A simple Model
  2. Regularization(L1/L2正则化，限制每个模型的参数能选择的值的范围)
  3. Bagging / STacking
Reduce Noise
  1. 统计学上不可降低；
  2. 在实际上可以通过提升数据质量，降低数据噪音等来实现提升。

上述技术叫做：集成学习。Ensemble Learning，是通过多个模型来提高效果。

Bagging⚓︎

  1. 每次训练 n 个模型，但是每个模型独立训练（in parallel）
  2. 分情况：
  3. 如果是回归模型，那么，结果就是把 \(n\) 个模型的预测结果进行平均，得到最后的结果；
  4. 如果是分类，那就是Majority Voting，按照投票最多的那个进行分类；
  5. 每个模型都是通过 Bootsrtap Sampling 的方式进行训练的。

比如，我需要 \(m\) 个样本，那我从所有的样本中带放回地采样 \(m\) 次 (Sample with replacement)。

这意味着有的样本可能被拿了多次，有的样本可能一次也没拿到。每次拿到的样本都是有一定不同的。

  • 大概每次会采样 63 % 的样本。剩下的样本就可以作为验证集，看看 Bagging 的效果如何。
class Bagging:
    def __init__(self, base_learner, n_learners):
        self.learners = [clone(base_learner) for _ in range(n_learners)]
        # 复制是因为每个小模型之间是不能share权重的
    def fit(self, X, y):
        for learner in self.learners:
            examples = np.random.choice(
                np.arange(len(X)), int(len(X)), replace=True)
                # 进行随机采样
            learner.fit(X.iloc[examples, :], y.iloc[examples])
    def predict(self, X):
        preds = [learner.predict(X) for learner in self.learners]
        # 对每一个learner(小模型)都进行一次预测
        return np.array(preds).mean(axis=0)

Random Forest(最重要的应用)⚓︎

  • Use Decision Tree as base learner
  • Often randomly select a subset of features for each learner. (也就是选择列的时候也带有随机性)

Apply Bagging in unstable learner⚓︎

Bagging 的效果是降低了方差，但是没有改变偏差。 改善了泛化误差中的一项。这也是为什么可以一直增加Base learner的个数。

但是增加Base learner不一定总能带来效果的增加。

  1. 采样一次和采样N次取平均，Bias是不会变的，但是会带来方差的减小。
  2. 一般而言，方差比较大的时候，Bagging效果会比较好；也就是 Unstable Learner 的时候效果比较好。(Bagging reduces model variance, especially for unstable learners)
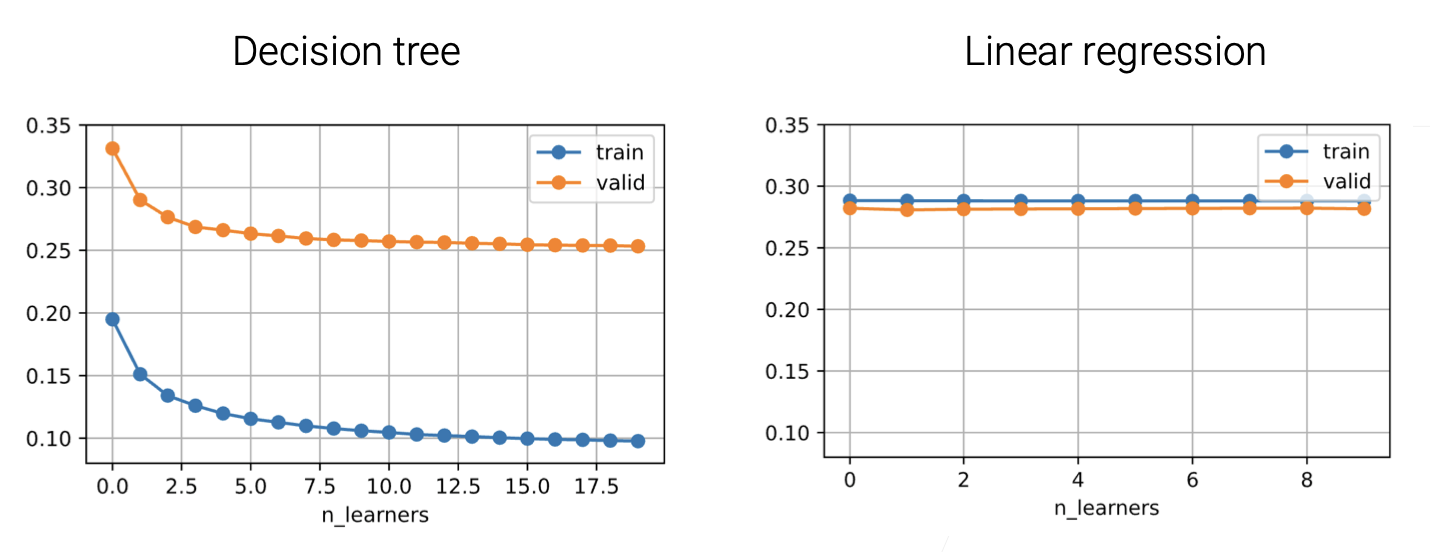
  3. 比如说，决策树就是一个不那么稳定的模型，因为数据发生变化了，每次选取特征进行分支的时候就会不一样。这就很适合用Bagging；而线性回归，因为可以写成显式解，那其实是比较稳定的。以下是对比。

Boosting⚓︎

目标是降低偏差Bias。是通过对多个较弱的模型按顺序训练，得到一个更强的模型。

Learn n weak learners sequentially, combine to reduce model bias

在第 \(i\) 步，训练完弱模型\(h_i\)后，根据弱模型的样本误差 \(\epsilon_i\)，根据误差评估，重新采样效果不好的样本进行训练，使得下一个模型会更加注意效果不好的那些样本。

Adaboost, Gradient Boosting.

Gradient Boosting⚓︎

\(H_t(x)\): output of combined model at timestep \(t\)

初始时刻，我们是在原始样本上进行训练。\(H_1(x) = 0\)；

在后续的每个 \(t\) 时刻，我们训练模型 \(\hat{h}_t\)，这是根据残差进行训练(Train on residuals). \(\{ (x_i, y_i - H_t(x_i)) \}_{i = 1,...,m}\)。

然后模型融合： \(H_{t+1}(x) = H_t(x) + \eta \hat{h}_t(x)\). 这里的 \(\eta\) 是学习率, 也是(Shrinkage parameter)，避免过拟合。

如果选择 MSE 为损失函数

\(L= \frac{1}{2} (H(x) - y)^2\)，此时残差等于负梯度方向。 \(y - H(x) = - \dfrac{\partial L}{\partial H}\)

对于其他的Loss L，我们有：\(\hat{h}_t = \arg \min \dfrac{1}{2} (\hat{h}_t(x) + \dfrac{\partial L(x)}{\partial H_t})^2\)

避免过拟合：Subsampling, Shrinkage, Early stopping.

class GradientBoosting:
    def __init__(self, base_learner, n_learners, learning_rate):
        self.learners = [clone(base_learner) for _ in range(n_learners)]
        self.lr = learning_rate
    def fit(self, X, y):
        residual = y.copy()
        for learner in self.learners:
            learner.fit(X, residual)
            residual -= self.lr * learner.predict(X)
            # 残差 减去 预测值 * 学习率
    def predict(self,X):
        preds = [learner.predict(X) for learner in self.learners]
        return np.array(preds).sum(axis=0) * self.lr

Gradient Boosting Decision Tree (GBDT)⚓︎

GB 是很容易过拟合的。需要我们尽可能用一些比较弱的模型，同时设置较低的学习率。

  • Use decision tree as the weak learner（虽然决策树本身不弱，但是可以设置得参数较弱一点）

    Regularize by a small max_depth and randomly sampling features

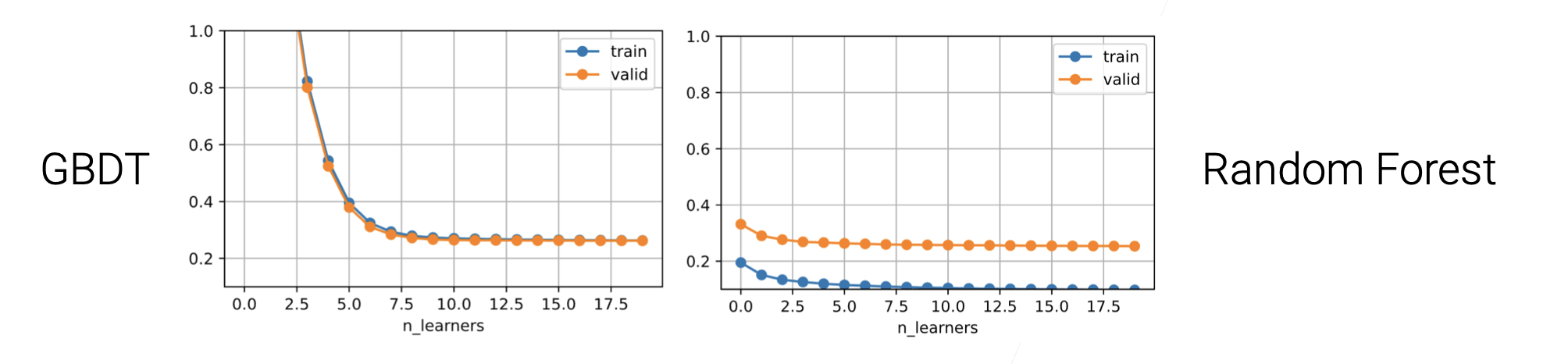
问题

需顺序地训练模型。速度和效率比较慢。所以通常会用到XGBoost, LightGBM, CatBoost等工具。可以加快模型训练速度。

SUMMARY

  • Combine to reduce bias.
  • GB: reduce bias by fitting residuals.

Stacking⚓︎

和Bagging有类似之处。把不同的小模型混合起来降低方差。

区别：

  1. 每个模型是不同类的模型，比如MLP, GBDT, Random Forest等。 在同一个数据集上训练不同的模型。
  2. 每个模型都是在所有样本上进行训练，不需要Bootstrap重新采样（因为一些小模型本身就已经重新采样了）；
  3. 线性地将每个模型的结果取平均，或者加权重，或者投票。本质上这个权重可以学习的。可以加一个全连接层。输入大小是模型数量 \(n\)，输出维度是 1 。

  • Linearly combine base learners outputs by learned parameters

  • widely used in competition.

很多时候，有的模型效果不是那么好，就没有必要把这个结果加入Stacking中了。

Multi-layer Stacking⚓︎

Stacking也可以用来降低偏差。

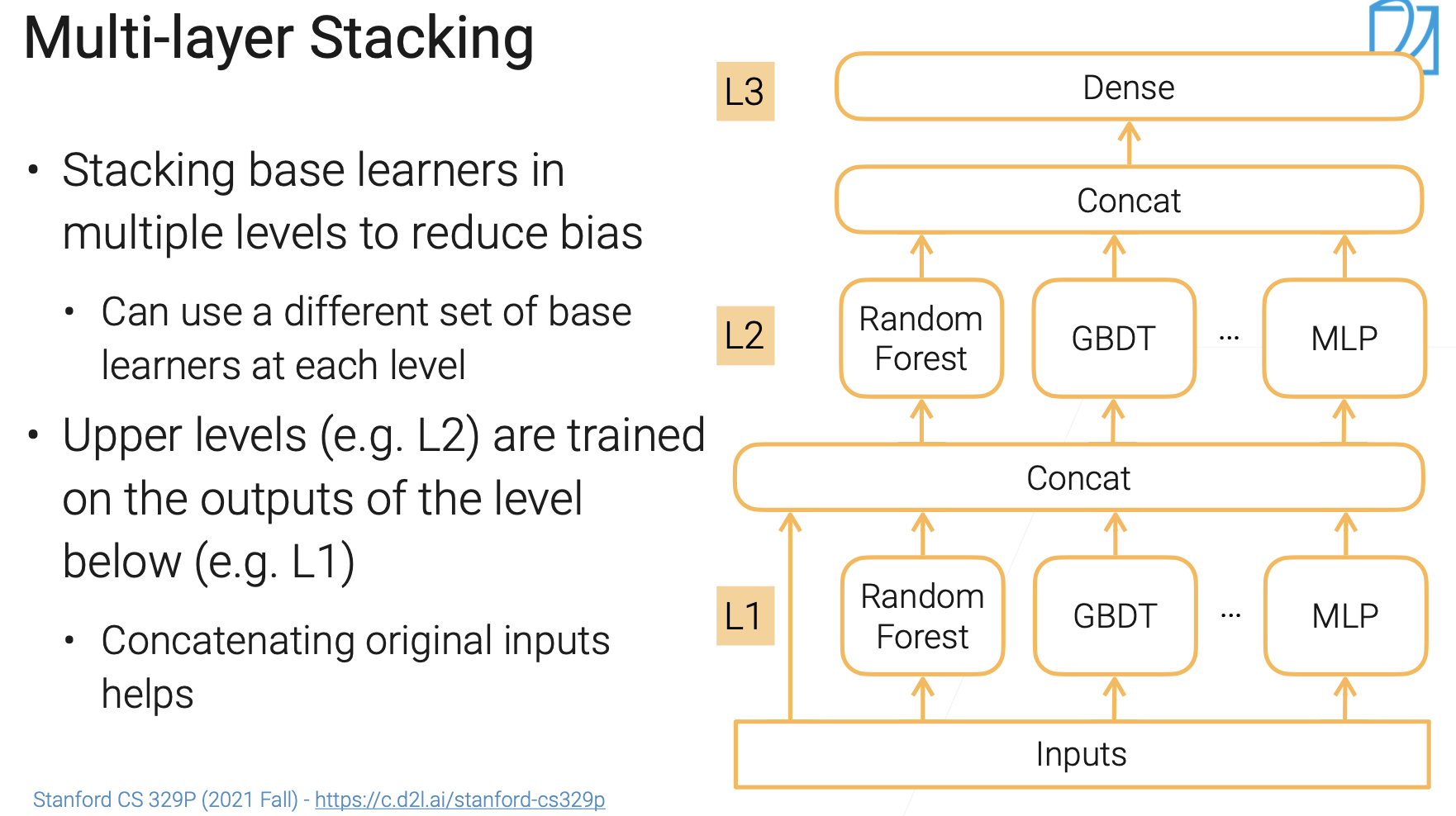
第一层，假设 \(n\) 个模型，就会有一个长为 \(n\) 的向量。把这个向量视为一个特征，进入下一层。

一般而言，进入下一层的输入 = 上一层的结果 + 上一层原始的输入。就类似一个MLP.

每一层可以使用不同的模型组合。

多层 Stacking 特别容易过拟合。这是因为数据进来做过一次训练，又把这个预测传入进来放到下一层的话，很容易学到之前可能是噪音的地方学习起来。

如何避免多层Stacking的过拟合⚓︎

  1. 训练第一层和第二层的不应该是同一份数据：将训练集分成A，B两块，先在第一层用A进行训练，然后在B上进行预测，产生的预测结果，加上B的本身，作为第二层模型的训练。这样可以使得训练集不会耦合在一起。

repeated K-fold bagging（有一点困惑）

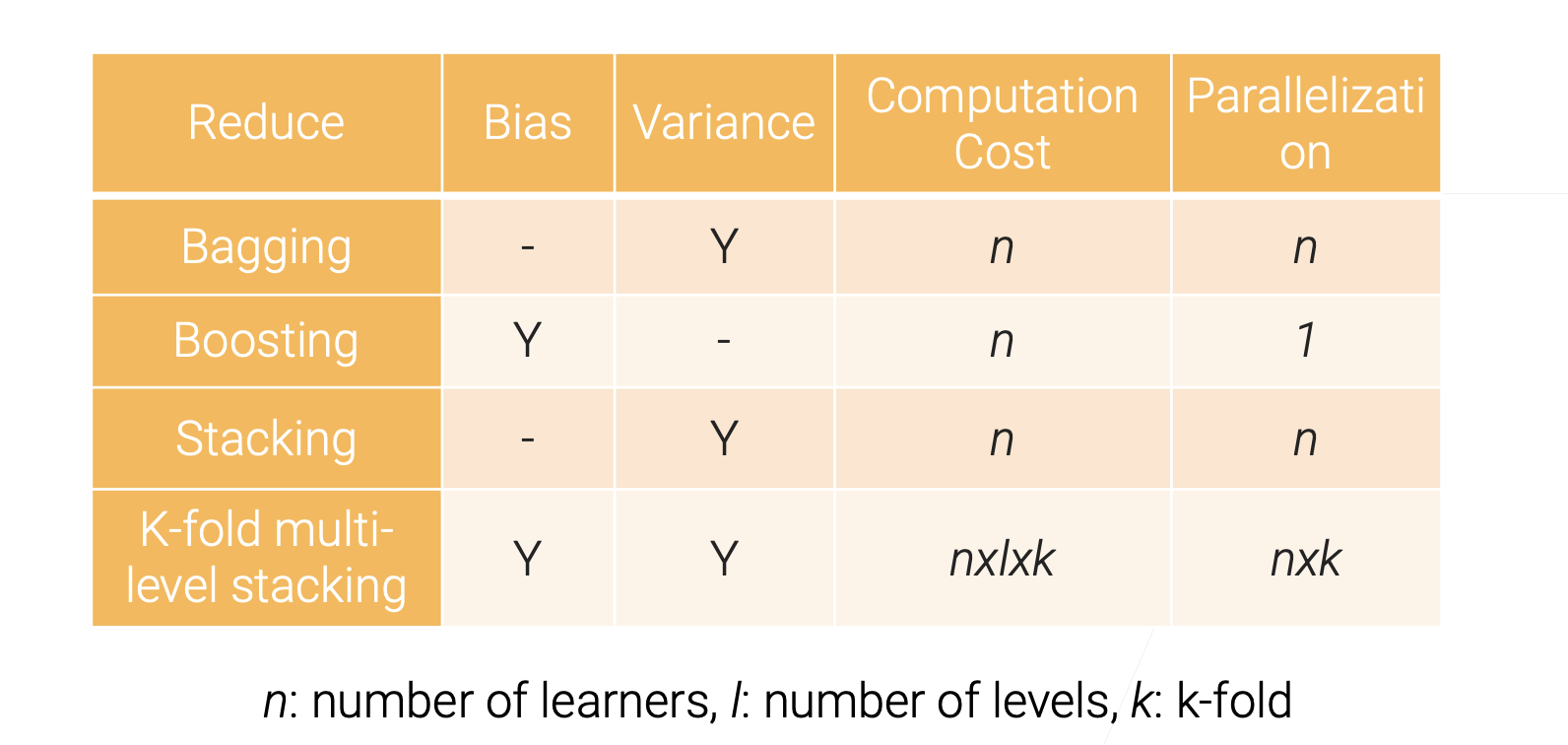
  1. 与k-fold交叉验证一样，分成K份；每次在 \(K-1\)份上训练，在i-th上进行验证
  2. 假设 i-th fold进行验证，那么我们把在这个fold上的输出留下来；\(k\) 个fold得到 \(k\) 个输出，这样这 \(k\) 个小fold里实际上是 \(n * k\) 的小模型。
  3. 将前两个步骤重复 \(n\) 次。将每个样本里的结果取平均放入下一层的训练中。

目的是保证每一层的训练数据不会和上一层的数据混合在一起。

9.1 超参数调参⚓︎

手动调参(Manual Hyperparameter tuning)：⚓︎

  1. 从一个好的基线开始（Baseline），一般可以选一些高质量的工具包里的默认数值，也可以看到Paper中的一些值；
  2. 调整某个值，重新训练模型，查看这个值对模型的影响如何。
  3. 重复上述过程，获得一些好的Insights. 比如：
  4. 哪个参数比较重要；
  5. 哪些超参数是比较敏感的；
  6. 哪些参数范围是比较好的；

小例子：SGD和Adam优化器，效果会存在差异。

记得记录一下每次调参的结果。Log your experiment!
可以用tensorboard等进行可视化的展示

Reproduction is hard!

自动调参(Automated parameter tuning)⚓︎

  • AutoML: Automated Machine Learning : 机器学习算法在解决实际问题的时候都自动化；但是在从实际案例中抽取问题、数据清理上起到的作用很有限；

应用

  • 模型超参数优化Hyper Parameters Optimization (HPO)，通过搜索算法找到一个好的超参数集合；

  • 网格架构搜索 Neural Architecture Search：

9.2 超参数优化⚓︎

我们在什么搜索空间里寻找超参数？

训练算法

  • blackbox：每一个任务当作一个黑盒。每调一个超参数就进行训练，训练好了之后，把精度和误差返回给我，以此来看效果如何。
  • Multi-fidelity(多置信)。不需要完整训练整个数据集，我只需要关注哪个超参数比其他的超参数更好，关注的是超参数之间的排序。这里可以用一个近似值进行排序。比如可以对数据集采样10%，进行训练；可以减小模型大小（比如通道数、层数等）；比如提前停止训练等；

最常见的搜索策略。网格搜索，暴力穷举。

for config in search_space:
    train_and_eval(config)
return best_result
  • All combinations are evaluated
  • Guarantees the best results
  • Curse of dimensionality
for _ in range(n):
    config = random_select(search_space)
    train_and_eval(config)
return best_result

最多尝试 \(N\) 次。比 Grid Search 更加 Efficient，一般N取决于你手头的资源，或者想要训练的时间。

Bayesian optimization⚓︎

相对比较复杂，但是很Active.

BO会学习一下从超参数到你的损失函数之间的函数。（与之相对的，机器学习学习的是数据到label的一个映射）。每做一个实验得到一个数据点，会根据当前的一些评估选择下一个去尝试的超参数。

Sorrogate model

未完待续。