推荐系统⚓︎
约 9077 个字 14 张图片 预计阅读时间 30 分钟 总阅读量 次
王树森的推荐系统课程,学习笔记。
Lecture 1. 概述⚓︎
- 小红书的推荐系统
-
笔记 -> 用户点击 -> 用户操作。
- 曝光 (Impression)
- 点击 (Click)
- 滑动到底 (Scroll to end)
- 点赞 (Like)
- 收藏 (Collect)
- 转发 (Share)
- 评论 (Comment)
- 消费指标
-
点击率 = 点击次数 / 曝光次数
点赞率 = 点赞次数 / 点击次数。 (收藏率 / 转发率 等类似)
阅读完成率 = 滑动到底次数 / 点击次数 \(\times\) \(f\)(笔记长度)
需要考虑笔记长度,否则对长笔记不公平。
- 消费指标不是衡量推荐系统的根本指标。 一味追求这些指标是不对的。缺少多样性会导致用户失去兴趣,导致用户流失;而更多的多样性可能可以留住用户,让用户更活跃。
- 北极星指标
-
用户规模:日活用户数 (DAU) / 月活用户数 (MAU): 不论一天/月使用几次,只要登陆了,都算一个日/月活。
消费:人均使用推荐时长、人均阅读笔记的数量:看一天看了多长时间的小红书/多少个笔记。
如果北极星指标和消费指标冲突,那么以北极星指标为准。北极星指标更重要。
发布: 发布渗透率、人均发布量。
- 实验流程
-
离线实验:收集历史数据,在历史数据上测试。没有部署到产品端,没有用户交户。
小规模A/B测试:部署到实际产品中。用户分组,一组用实验组,一组对照组。看效果是否有显著差异。
全流量测试:推到全流量中。
Lecture 2. 推荐系统的链路⚓︎
召回⚓︎
第一步,从物品数据库中快速取回一些物品。
i.e., 用户刷新时,系统从各个召回通道取回几千篇笔记。
常见的召回通道包括==协同过滤、双塔模型、关注的作者==等。每个召回通道返回几十或者几百个笔记。总共有几千个笔记。
对于这些笔记融合、过滤,筛选掉用户不喜欢的笔记、作者、话题等。
粗排⚓︎
用规模较小的ML模型给几千个笔记进行打分。按照分数排序和截断,保留分数高的笔记。
因为直接用NN对上千个打分计算量太大。
精排⚓︎
用大规模深度神经网络给粗排的几百个笔记进行打分。分数反应用户的兴趣。可以截断也可以不做。
用到的参数量更大,准确性更高,用的特征。
示例
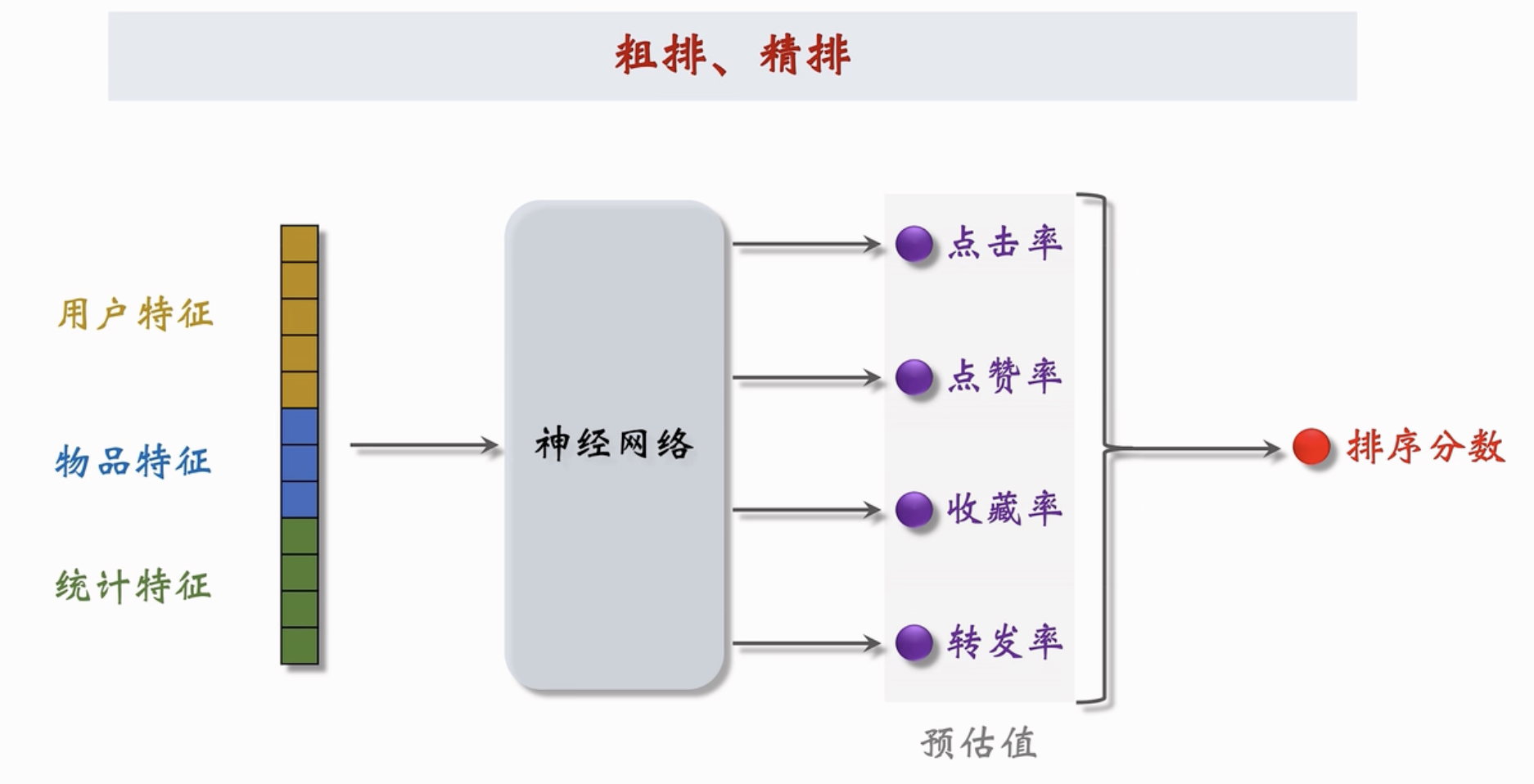
神经网络会输出很多数值。都是对顾客行为的预估。把这些预估值进行加权和。每个笔记都有多个预估分数,加和得到这个笔记的最终得分。
重排⚓︎
根据精排分数和多样性分数进行随机抽样,得到几十个笔记,然后打散并插入运营内容和广告等。
展示给用户的内容。
多样性抽样
MMR, DPP, 从几百篇中选出几十篇。然后用规则打散相应内容。不能将过于相似的内容排在同样的位置上(比如 1~5 都是 NBA 笔记,此时就要调整)、比如插入相关的广告、运营内容等。
召回和粗排是最大的漏斗,能够将候选笔记的数量从几亿 -> 几万 -> 几百
Lecture 3. A/B测试⚓︎
所有对模型和策略的改进都需要经过线上A/B测试,用实验数据验证策略和模型是否有效(在业务指标上有提升)。
A/B测试还能够帮助选择一些参数。比如神经网络的层数等。
随机分桶⚓︎
将 \(n\) 个用户分成多个桶。用哈希函数将用户ID映射到某个空间内的整数中。把这些整数均匀地分成 \(b\) 个桶。
i.e., 分成10个桶,#1,#2,#3 中的用户在召回时,分别用新策略的3个不同参数,#4 作为对照组。如果某个桶的效果更好,则说明可以采纳这个桶的参数下的新策略。
分层实验⚓︎
解决“流量不够用”的问题。
公司有很多部门(推荐、用户界面、广告),部门有不同的组。大家都需要做A/B实验。如果只分10个桶,很难满足大家产品迭代的要求。
分层实验:把实验分很多层,包括召回、粗排、精排、重排、广告、用户界面等。每个部门对这一层的用户进行处理。
同层互斥:某个召回组使用了4个桶,那么剩下的组只能用剩下的 \(b - 4\) 个桶。这是为了避免一个用户同时受两个策略影响。
不同层正交:每一层独立随机对用户作分桶。不同层的实验可以有重叠的用户。每一层都可以对100%的用户进行实验。i.e., 召回层和粗排层的重合会很小。
正交 vs 互斥
如果所有实验都正交,那么可以同时做无数个实验。
- 用互斥是因为一些模型结构(比如精排)天然就是互斥的。
- 同类的策略(比如2个召回通道)效果互相增强 / 互相抵消。互斥可以避免这种行为。
- 不同类的策略(召回&精排)通常不会互相干扰。可以作为正交的两层。
Holdout机制⚓︎
涉及如何考察一个部门在一段时间内对公司业绩的提升。
取10%的用户当作Holdout桶。推荐系统使用剩余90%的用户做实验,二者互斥。10%用户(holdout桶)vs 90%用户 (这里需要归一化) 为整个部门的收益。
每个考核周期结束后,清除 holdout 桶。推全实验从 90% 用户扩大到100%用户。然后重新建立 Holdout 桶。
实验推全&反转实验⚓︎
实验推全: i.e., 20%的用户受到某策略A/B测试影响。测试有效。此时删除这两个桶,把这个策略在除了Holdout桶的其他用户上推全,也就是新开一个层。
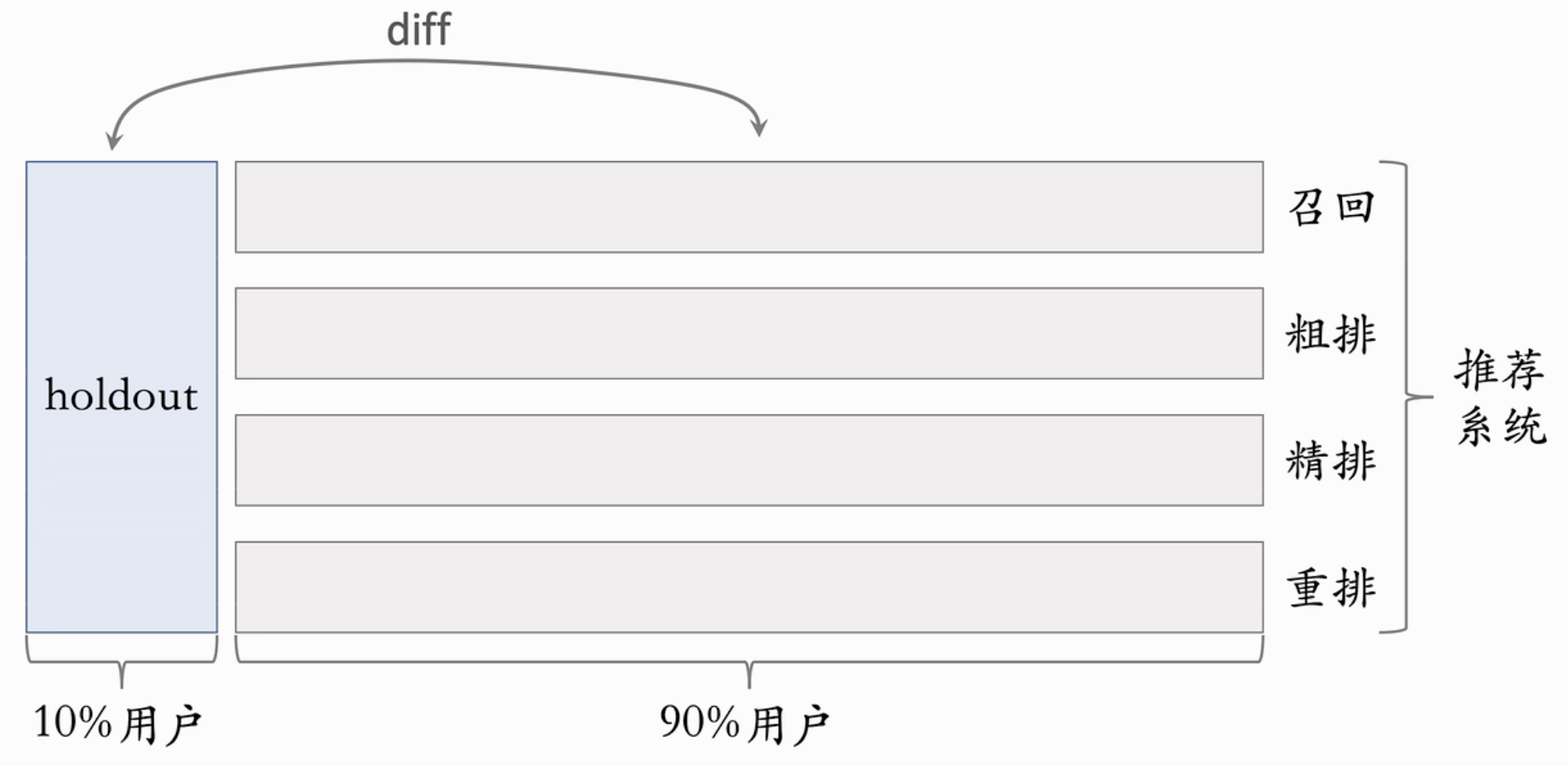
反转实验 :有的指标(点击、交互)能立即观察到新策略影响;有的指标(留存、转化)需要观察一段时间才能看到效果。而实验观测到收益后希望尽快开展新的实验。目的是开展新实验或者基于新策略进行开发。此时,如何处理这种“需要观察一段时间”和“立刻新测试”之间的矛盾。
解决办法:在推全的新层中开一个旧策略的桶(反转桶)。长期观测实验指标。
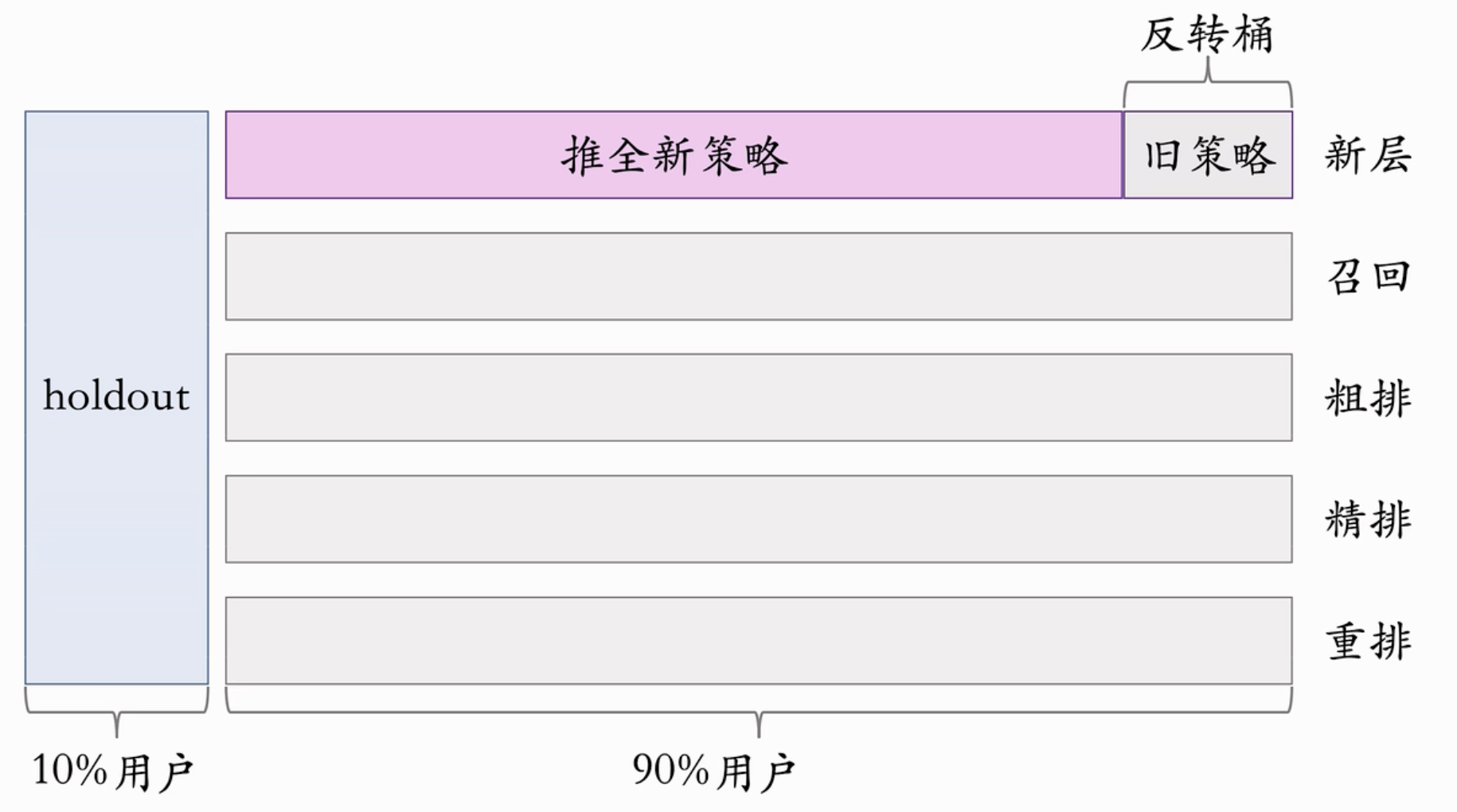
注意,一个研发周期后,新策略(正处在观察中的)也被应用到Holdout桶中了,但是新层中的反转桶不受影响。 反转实验完成时,关闭反转桶,实现真正的推全。
Lecture 4. 基于物品的协同过滤 (ItemCF)⚓︎
CF: Collaborative Filtering, 协同过滤。
原理
我喜欢A物品。 A和B物品很相似。我没有用过B物品。
那么系统会推荐B物品给我。因为它们很相似。
但是,系统怎么知道A和B很相似?
基于知识图谱、基于物品属性、基于用户行为 等。
Item CF的实现⚓︎
- 对于用户交互过的物品 \(j\)
- 可以记录用户对这些物品的兴趣: \(\text{like} (\text{user}, \text{item}_j)\) (通过点赞、收藏、评论等行为)。比如: \([2,1,4,3]\)
- 对于用户没有交互过的物品 \(i\)
- 可以记录这个物品和交互过的物品的两两相似度. \(\text{sim} (\text{item}_i, \text{item}_j)\),比如 \([0.1, 0.4, 0.2, 0.6]\)
我们可以预估用户对物品的兴趣:
\[\sum_j \text{like} (\text{user}, \text{item}_j) \times \text{sim} (\text{item}_i, \text{item}_j)\]
代入上面的数字:计算得这个物品的得分为 3.2。
物品相似度的计算⚓︎
两个物品的受众重合度越高,说明物品越相似。反之,如果用户不重合,说明物品不相似。
记喜欢 \(i_1\) 的用户集合 \(W_1\), 记喜欢 \(i_2\) 的用户集合 \(W_2\)。定义交集 \(V = W_1 \cup W_2\)。
物品相似度:
\[\text{sim} (i_1,i_2) = \dfrac{|V|}{ \sqrt{|W_1| \cdot |W_2|}}\]
(数值在0~1之间)
但是没有考虑用户喜欢物品的程度。只有 0/1。为了弥补这个问题,我们将相似度取为:
\[\text{sim}(i_1, i_2) = \frac{\sum_{v\in V} \text{like} (v, i_1) \cdot \text{like}(v, i_2)}{\sqrt{\sum_{u_1\in W_1} \text{like}^2(u_1, i_1)} \cdot \sqrt{\sum_{u_2\in W_2} \text{like}^2(u_2, i_2)}}\]
分子表示同时喜欢两个物品的人数的兴趣分的乘积。 分母第一项是所有用户对物品1的兴趣分的平方开根号,分母第二项是所有用户对物品2的兴趣分的平方开根号。
这个就是余弦相似度。可以把每一个Item都表示为一个稀疏向量。每个向量都对应一个顾客(的兴趣分),这两个向量的余弦值就是这两个Item的相似度。
我们事先需要知道每两个物品之间的相似度并保存起来。
ItemCF的完整流程⚓︎
为了线上做推荐,必须事先做离线计算。
- 建立“用户-物品”的索引。
-
记录每个用户点击、交互过的物品ID。
这样给定任何顾客,都可以找到ta近期感兴趣的物品列表。
- 建立“物品-物品”的索引。
-
计算物品两两之间的相似度。
对于任意物品,索引它最相似的 \(K\) 个物品。这样给定任意物品,可以找到距离它最近的 \(K\) 个物品。
线上做召回
- 给定用户ID,通过 用户-物品 索引,找到用户近期感兴趣的物品列表,共 n 个物品。
- 对于每个物品,找到与它最接近的 k 个物品 (top-k)。
- 对于取回的所有物品 (最多 \(nk\)) 个,用公式预估用户对物品的兴趣分数。
- 返回分数最高的100个物品,作为召回结果。
索引的作用在于避免枚举所有的物品。用索引,离线计算量大,但是在线计算量小,可以实时推荐。这个场景可以描述为:
用户登录后,系统需要为用户做推荐,此时根据ID找到用户最近浏览/感兴趣的物品,得到其兴趣分数。然后从这些物品出发,找到每个物品的相似物品(Top-K),得到 \(nk\) 个物品。这里可能有重复的内容,要去重,把分数加起来。。然后对于这些物品,计算用户对该物品的兴趣,注意,这里要计算这个物品与所有“感兴趣物品”的相似度,再对应乘以感兴趣商品的兴趣分,最后求和,不是只计算这个物品和“得到这个物品的那个感兴趣物品” 之间的得分。
ItemCF是一个非常重要和主要的召回通道。
Lecture 5. Swing 召回通道⚓︎
同样在工业界很常用,区别在如何定义物品之间的相似度。
Item CF认为,如果有大量的用户喜欢两个物品,那么这两个物品之间有较高的相似度。
ItemCF 的不足
如果重合的用户是一个小圈子:
笔记A和笔记B没有什么相似之处,受众差距很大,但是被分享到同一个微信群中,导致一段时间内很多用户均点击了这两个笔记,从而错误判断两个笔记的相似度。
我们希望降低小圈子用户的权重,如果某个小圈子用户同时交互两个物品,不能认为它们很相似;反之,如果大量不相关用户交互了两个物品,则可能说明它们之间有相同受众。
我们定义 \(u_1\) 用户喜欢的物品集合 \(\mathcal{J}_1\); \(u_2\) 用户喜欢的物品集合 \(\mathcal{J}_2\);定义重合度:
\[\text{Overlap} (u_1, u_2) = | \mathcal{J}_1 \cup \mathcal{J}_2 |\]
如果2个用户之间的重合度高,那么他们可能来自一个小圈子,要降低他们的权重。
我们把喜欢物品 \(i_1\) 的用户记作集合 \(W_1\),我们把喜欢物品 \(i_2\) 的用户记作集合 \(W_2\)。定义交集: \(V = W_1 \cap W_2\)。
两个物品的相似度:
\[\text{sim}(i_1, i_2) = \sum_{u_1 \in V} \sum_{u_1 \in V} \dfrac{1}{\alpha + \text{overlap}(u_1, u_2)}\]
也就是,同时喜欢两种物品的人的重叠度的倒数。此处的 \(\alpha\) 是人工设置参数。
于是可以降低小圈子对相似度的影响。
Lecture 6. 基于用户的协同过滤:UserCF⚓︎
UserCF原理⚓︎
有很多和我兴趣相似的网友。某个和我兴趣相似的网友点赞、评论、转发了某个笔记,但是我还没有看过这个笔记,那么系统就会给我推荐这个笔记。也就是,根据用户的相似度做推荐。
如何找到和我兴趣相似的用户?
- 点赞收藏转发的笔记有很多重合;
- 关注的作者有很大重合。
UserCF的实现⚓︎
用户 \(i\) 和其他用户 \(j\) 之间的相似度,比如有4个用户,和目标用户 i 的相似度 [0.9, 0.5, 0.5, 0.3]
\(\text{sim} (\text{user}_i, \text{user}_j)\)
用户 \(i\) 对物品的兴趣分数, 比如4个用户对同一个物品的兴趣:[0, 4, 2, 0]
\(\text{like} (\text{user}_j, \text{item})\)
预估用户对物品的兴趣
\[\sum_j \text{like} (\text{user}_j, \text{item}) \times \text{sim} (\text{user}_i, \text{user}_j)\]
带入上面4个数字,得到这个物品在 \(i\) 的兴趣分为 3。
注意,用户和用户之间的相似度是事先离线算好的,提前保存起来。
用户相似度的计算⚓︎
\[\text{sim}(u_1, u_2) = \frac{|I|}{\sqrt{| \mathcal{J}_1 | \cdot | \mathcal{J}_2 |}}\]
没有区别冷门和热门的物品。越热门的物品越无法反应用户的独特兴趣,反之,越冷门的物品,越能够反映用户的兴趣。
我们需要降低用户相似度中热门物品的权重。 可以将用户相似度的计算更改为:
\[\text{sim}(u_1, u_2) = \frac{\sum_{l\in I} \dfrac{1}{\log (1 + n_l)}}{\sqrt{| \mathcal{J}_1 | \cdot | \mathcal{J}_2 |}}\]
分子表示第 \(l\) 个物品的权重。这里的 \(l\) 用来标记每个物品。 \(n_l\) 表示喜欢这个物品的用户数量,反映物品的热门程度。
把每个用户表示成一个稀疏向量,每个元素就是一个物品。用户相似度就是两个用户向量夹角的余弦。
离线计算⚓︎
为了线上做推荐,必须事先做离线计算。
- 建立“用户-物品”的索引。
-
记录每个用户点击、交互过的物品ID。
这样给定任何顾客,都可以找到ta近期感兴趣的物品列表。
- 建立“用户-用户”的索引。
- 对于任意用户,索引它最相似的 \(K\) 个用户。这样给定任意用户,可以找到距离它最近的 \(K\) 个用户,并知道其相似度。
线上做召回
- 给定用户ID,通过 用户-用户 索引,找到用户最相关的 K 个用户;
- 对于每个top-k用户,找到他最感兴趣的 n 个物品 (last-n)。
- 对于取回的所有物品 (最多 \(nk\)) 个,用公式预估用户对物品的兴趣分数。
- 返回分数最高的100个物品,作为召回结果。
用户登录后,系统需要为用户做推荐,此时根据ID找到用户最相似用户(Top-K),对每个用户,取出其最感兴趣的 \(n\) 个物品,也就是总共 \(nk\) 个物品。这里可能有重复的内容,要去重,把分数加起来。然后对于这些物品,计算用户对该物品的兴趣,注意,这里要计算每个相似用户给这个物品的兴趣分,乘以相似用户和目标用户的相似度,最后求和。
Lecture 7. 离散特征的处理方法 (One-Hot 与 Embedding)⚓︎
离散特征:性别、国籍、用户ID、笔记ID等。
- 处理方法
-
- 建立字典:类别映射成序号;
- 向量化:
- 序号映射成高维稀疏向量;
- 序号映射成低维稠密向量,比如200个国家缩减为8维稠密向量。
One-hot编码⚓︎
男女。用 [0,0] 表示未知性别;[1,0] 表示男;[0,1] 表示女。
国籍。用长度200维的向量表示。每个国家只有一个元素是1,其他都是0.
如果类别数量很大,实践中一般不用 One-hot 编码。对于规模很小的离散变量,可以使用 One-hot 编码。
Embedding编码 (嵌入)⚓︎
比如,想要对国籍编码,将200个国家,映射到一个大小为 4 的向量。
参数数量 = 向量维度 \(\times\) 类别数量,也就是有800个参数。
编程实现的时候可以直接用Embedding层,参数以矩阵形式保存,矩阵大小就是:向量维度 \(\times\) 类别数量,输入就是一个序号,比如1,2,...,200,输出就是对应的向量,也就是参数矩阵的一列。
再比如,我们有10000个电影,以16维参数表示一个电影,那么有160,000个参数。Embedding参数很大很大,大多数神经网络参数都是Embedding层参数。深度学习系统会对Embedding层做很多优化。
再比如,词嵌入 (word embedding)等。
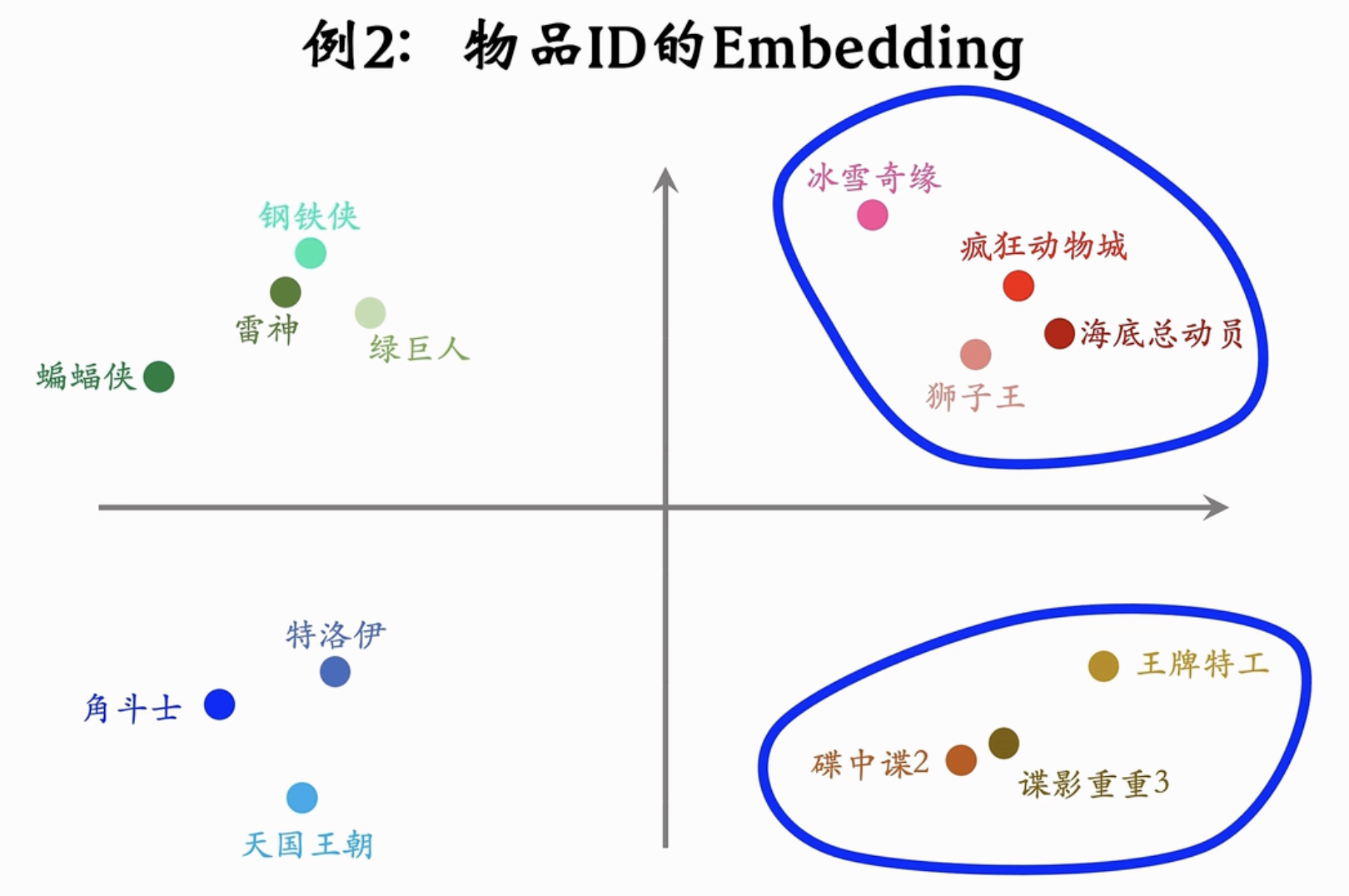
实际上,Embdedding = 参数矩阵 \(\times\) One-Hot向量。
Lecture 8. 向量召回:矩阵补充⚓︎
(Matrix Completion). 能够更好理解双塔模型。
我们基于前一节课的Embedding,可以这样进行推荐:
输入用户ID和物品ID,经过Embedding层后(这两个embedding层不共享参数),分别得到两个低维向量。 \(\textbf{a}, \textbf{b}\)。计算这两个向量的内积,就可以得到一个实数输出,也就是预估的用户对这个物品的感兴趣程度。
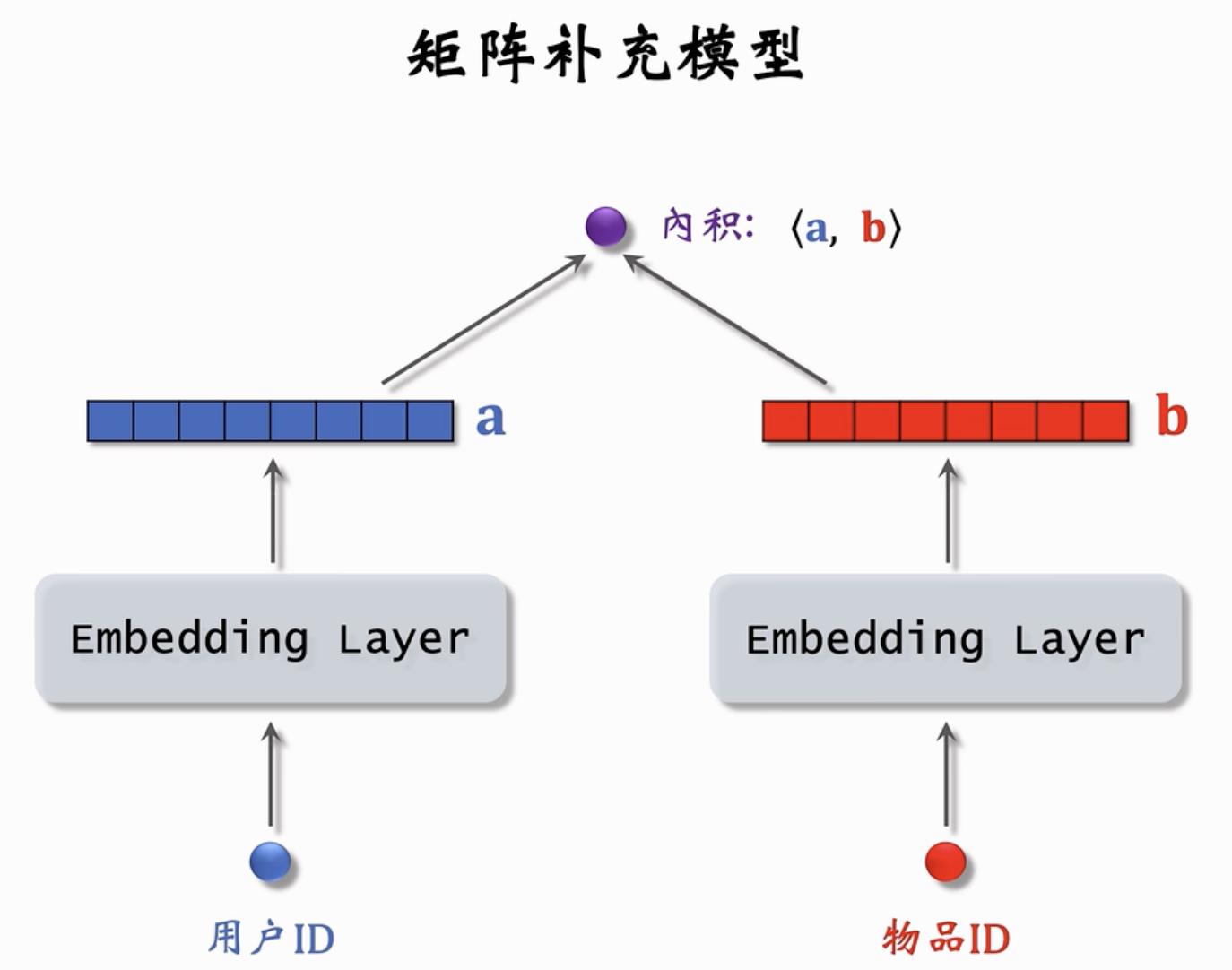
基本想法与流程⚓︎
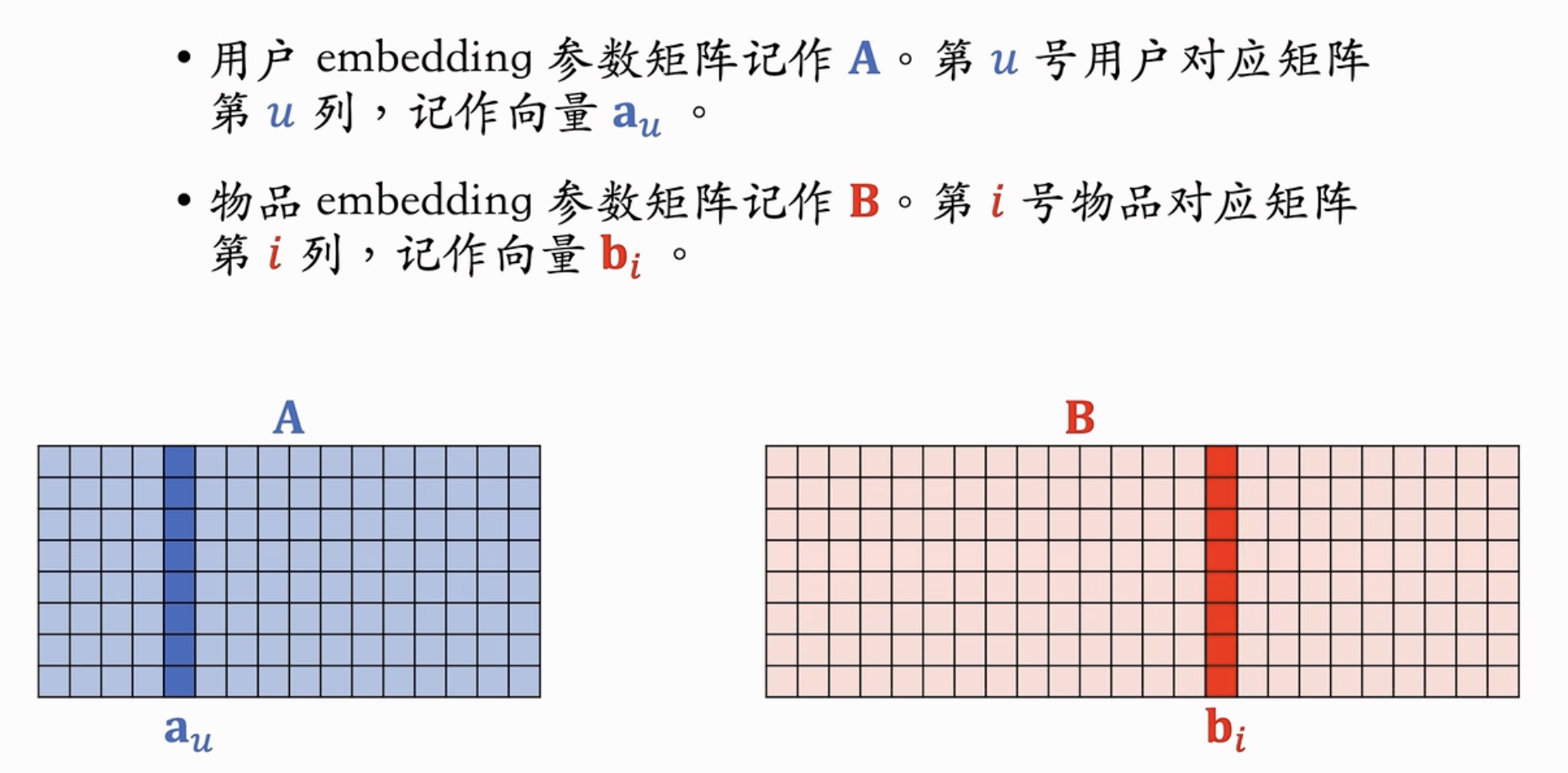
用户embedding参数矩阵 \(\mathbf{A}\),用户 \(u\) 对应第 \(u\) 列,记作向量 \(\mathbf{a}_u\)。
物品embedding参数矩阵 \(\mathbf{B}\),物品 \(i\) 对应第 \(i\) 列,记作向量 \(\mathbf{b}_i\)。
训练模型的目的是学习矩阵 \(\mathbf{A}\), \(\mathbf{B}\),使得预估值拟合真实观测的兴趣分数。
- 数据集
-
(用户, 物品, 兴趣评分) 三元组。记作 \(\Omega = \{(u, i, y_{ui})\}\),其中 \(y_{ui}\) 表示真实的用户 \(u\) 对物品 \(i\) 的兴趣评分。
注意,这个 \(y\) 是真实记录的。只要曝光了就会记录。比如曝光都是0分,有点赞、转发、评论收藏则分别+1,也就是最多4分。
我们的任务就是求解这样一个优化问题:
\[\min_{\mathbf{A}, \mathbf{B}} \sum_{(u, i, y) \in \Omega} \left( y - \langle \mathbf{a}_u, \mathbf{b}_i \rangle \right)^2\]
我们希望最小化真实分数和预估分数之间的差的平方,也就是越小越好。
我们的决策变量就是参数矩阵 \(\mathbf{A}\), \(\mathbf{B}\),可以通过随机梯度下降,每次更新矩阵 \(\mathbf{A}\), \(\mathbf{B}\) 的一列。
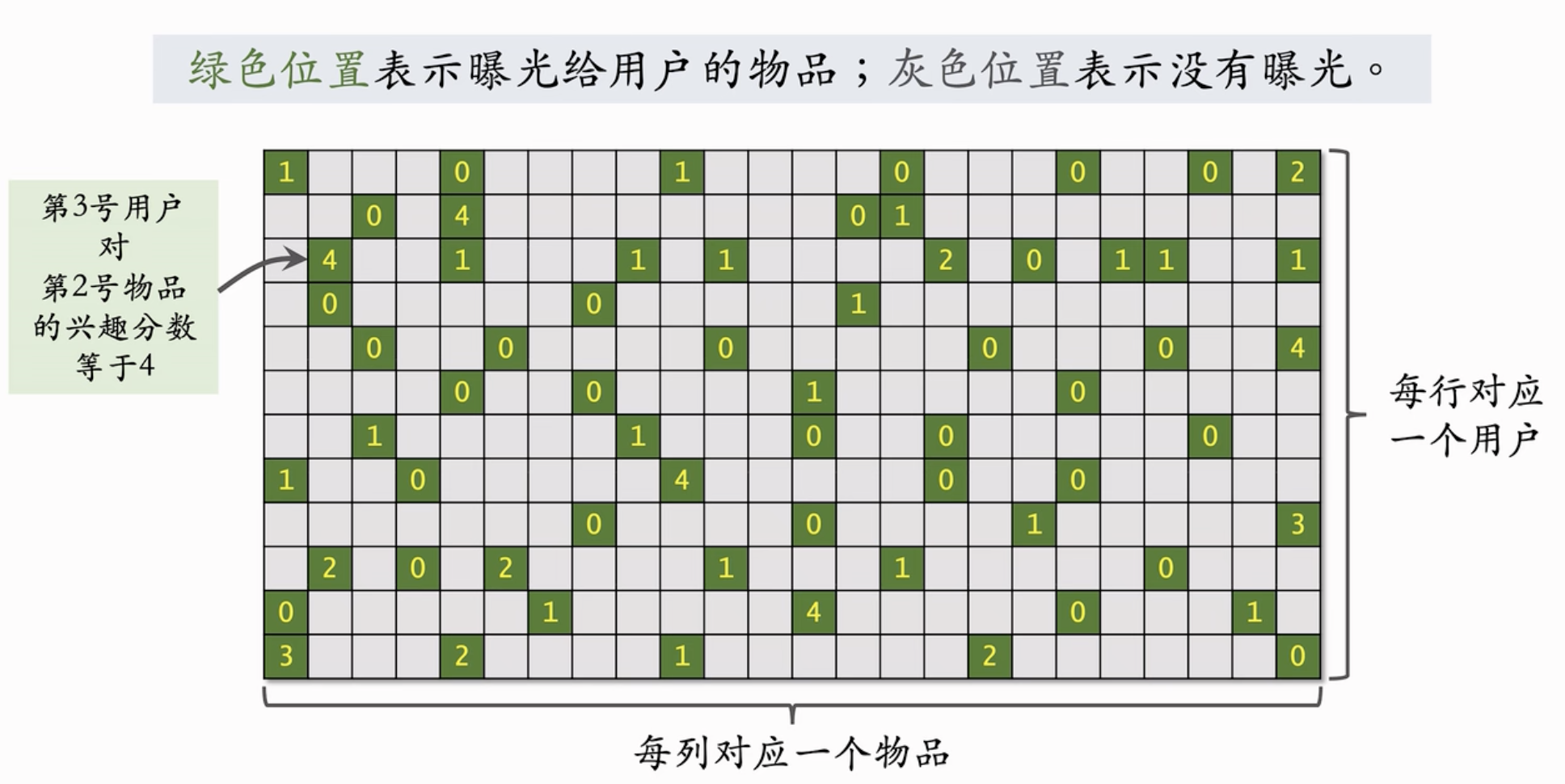
我们可以抽象成如上图所示的情况。每一行表示一个用户,每一列表示一个物品,最开始时候有真实情况下的打分,考虑到很多物品没有被曝光,矩阵中很多元素都是 0.
我们通过训练,得到 \(\mathbf{A}\), \(\mathbf{B}\) 的参数,取这两个矩阵中各1列,取内积,就可以得到上面那个用户 \(\times\) 物品矩阵中每一个未知格子的数字。取每一行中较大的元素推荐给用户即可。
并不是工业界中Work的方法。缺点:
- 仅仅利用了Embedding,没有利用用户行为(年龄、地区、感兴趣的东西)和物品信息(类目、关键词、作者信息)。
双塔模型可以当作矩阵补充的加强版。
- 负样本的选取不对。
正样本:曝光之后,有点击、交互的行为; (✅ 正确的做法) 负样本:曝光之后,没有点击、交互的行为; (❌ 错误的做法,不能依照此来选负样本);
-
训练的方法不好。
- \(\langle \mathbf{a}_u, \mathbf{b}_i \rangle\) 内积不如余弦相似度;
- 用平方损失函数(也就是回归),不如使用交叉熵(也就是做分类)
数据存储⚓︎
把矩阵 \(\mathbf{A}\) 用 Key-Value 进行存储。key是用户ID,Value是一列。能够实现给定用户ID,返回用户向量(也就是对应的embedding)。
矩阵 \(\mathbf{B}\) 的存储比较复杂。 后面再讲。
线上服务⚓︎
我们通过Key-Value快速查找到用户向量 \(\mathbf{a}\)。然后,我们需要通过最近邻查找,找到距离这个用户最近的 \(k\) 个物品(如果还记得,內积 \(\langle \mathbf{a}_u, \mathbf{b}_i \rangle\) 就是用户对物品的兴趣评估) ,作为召回结果。
如果需要枚举所有物品,时间复杂度过高:数亿个物品。无法进行线上实时计算。
近似最近邻查找 (Approximate Nearest Neighbor Search)⚓︎
衡量最近邻的指标:余弦相似度、欧氏距离(L2距离)、向量内积最大。如果不支持余弦相似度,很好处理:对向量做归一化,二范数都等于1,那么内积就等于余弦相似度。
我们要从一堆向量中找到和 \(\mathbf{a}\) 最相似的,可以先离线把数据划分成许多区域。比如,cos 相似度,划分结果就是扇形,欧氏距离,就是多边形。
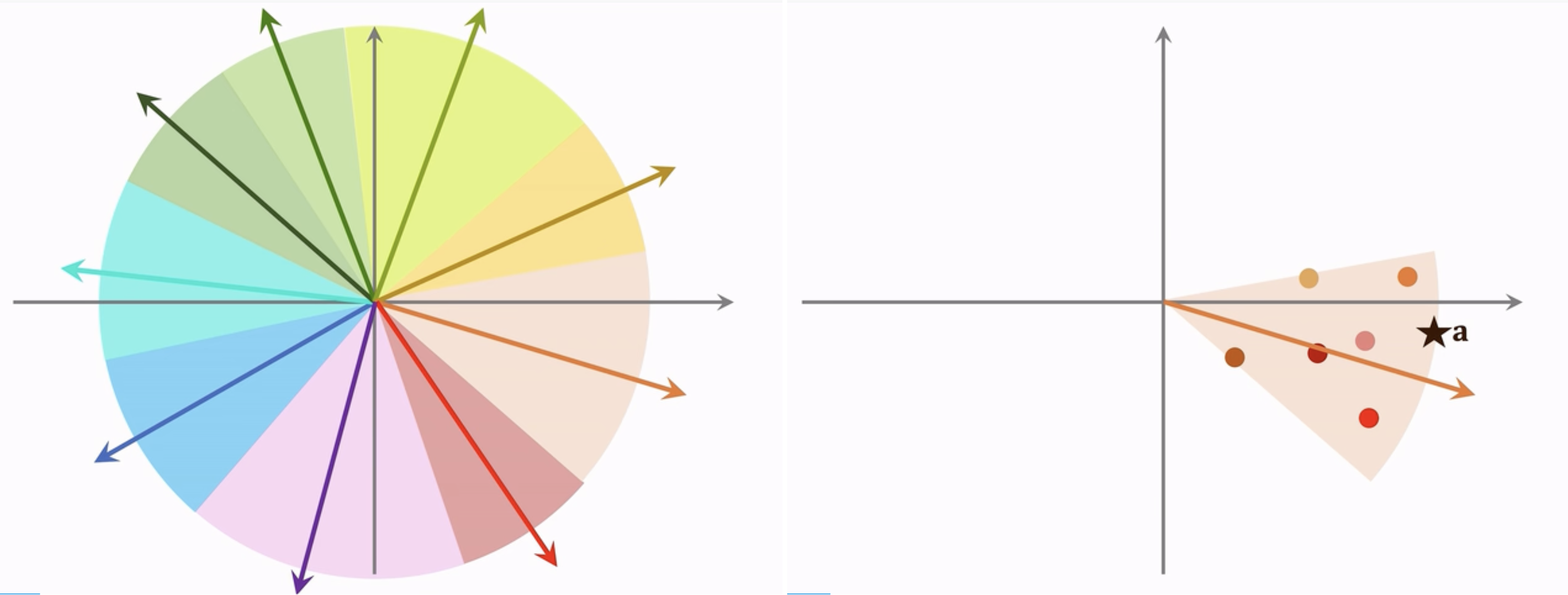
划分后 表示,然后建立向量索引。用一个向量代表这个区域,给定这个向量,就可以找到这个区域内所有的其他向量。
假如一亿个向量,划分一万个区域,每个区域就只有1万个。
我们可以找到和用户向量最相似的索引向量,然后根据这个索引向量得到1w个点,每个点对应一个物品。再对应查找即可。
总结一下:
我们用embedding后的用户向量和物品向量的内积来表示用户对物品的兴趣分。通过拟合真实观测的用户喜好,学习参数矩阵 \(\mathbf{A}\), \(\mathbf{B}\) 完成矩阵补充。基于矩阵补充的结果,用用户向量作为query,用近似最近邻查找,在线上找到用户最感兴趣的 \(k\) 个物品,作为召回的结果。
Lecture 9. 双塔模型⚓︎
包含了用户塔和物品塔,两个部分分开训练,用余弦相似度衡量相似性。可弥补了矩阵补充的缺陷:只用到了用户和物品的 ID,没有用到其他相关信息。
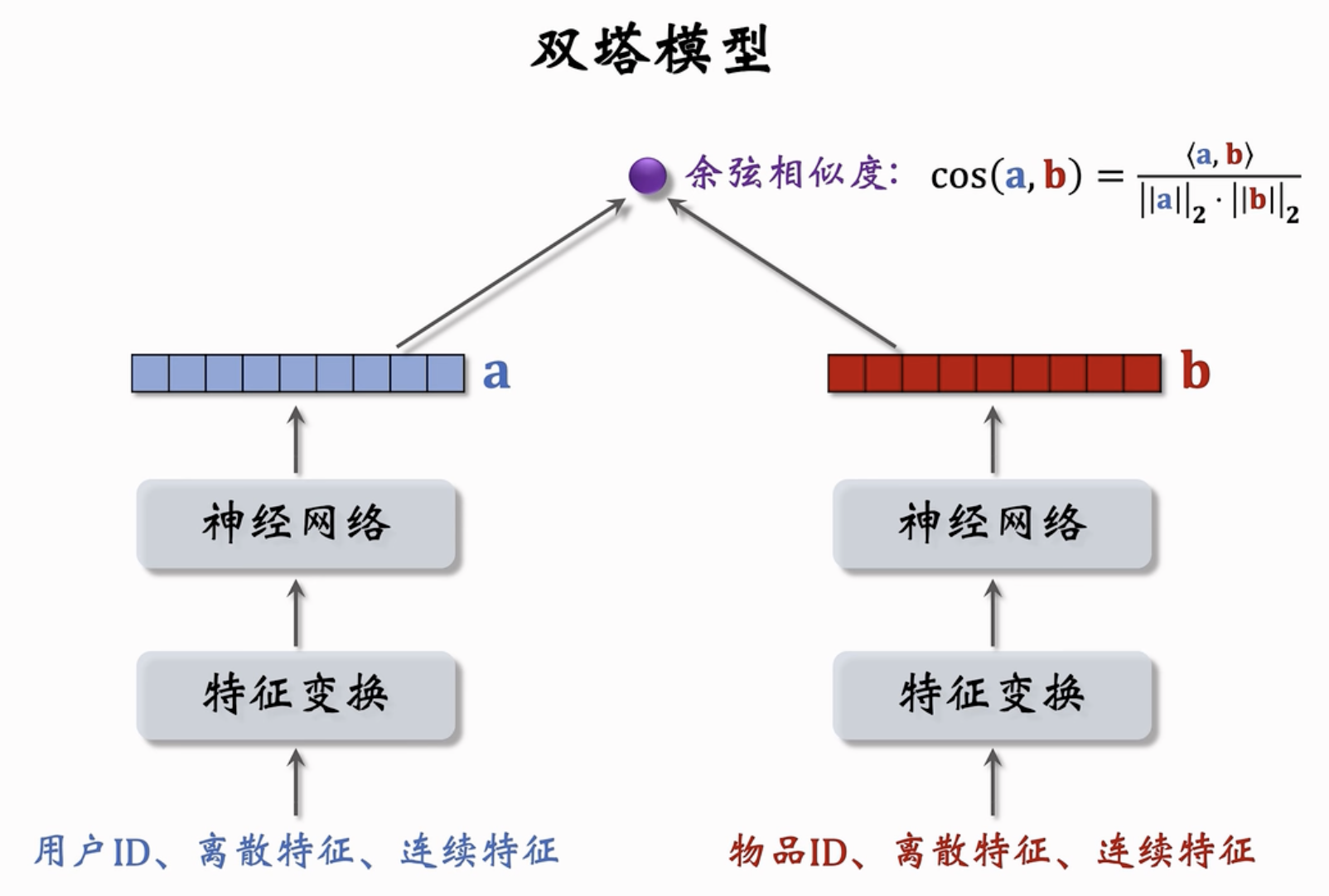
用户特征⚓︎
包括用户ID、离散特征、用户连续特征。
Embedding层把用户ID、离散特征、连续特征分别映射到向量中。注意,每一个离散特征(城市、感兴趣的话题)分别映射到一个embedding层;
对于性别之类的类型少的特征,可以直接用one-hot进行编码。
对于连续特征(年龄、消费金额、活跃程度等),可以用归一化处理,处理成特征mean = 0,std = 1;也可以进行分桶处理(比如常尾分布的,需要取log等);
上述所有的向量,我们concatenate起来,输入神经网络;神经网络的输出是一个向量,就是对用户的表征。
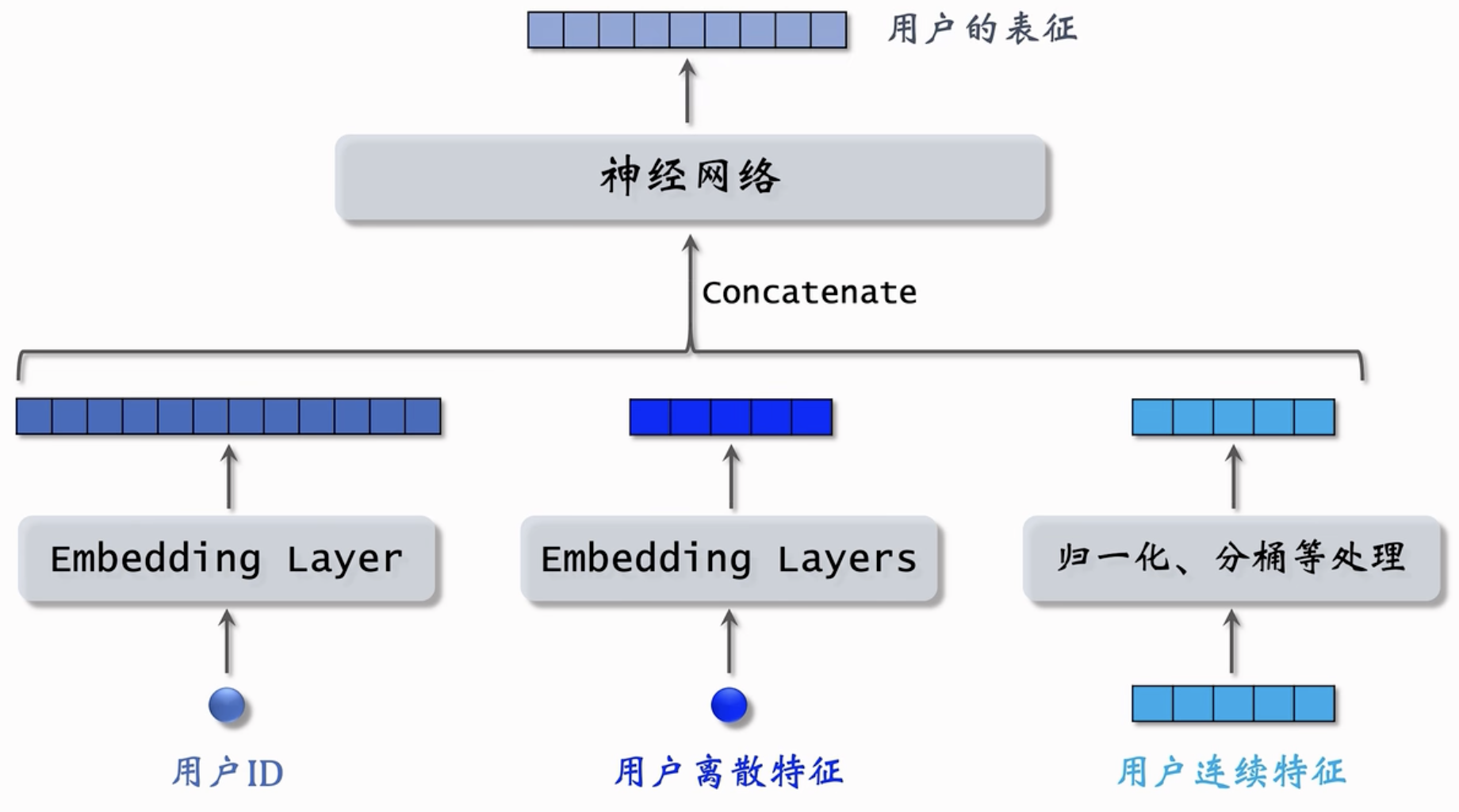
物品特征⚓︎
与用户特征的处理类似。首先用户ID可以映射成一个Embedding层;物品的离散特征也分别映射到一个Embedding层,形成多个向量;物品的连续特征也可以按照归一化、分桶、取log等进行映射。
得到的concatenate的特征向量输入神经网络,神经网络的输出是一个向量,就是对物品的表征。
把上述两个特征结合起来,就是双塔模型。每个塔除了ID外,还输入其他向量,分别表征其他特征;两个塔的输出结果求余弦相似度
\(\cos (\mathbf{a}, \mathbf{b}) = \dfrac{\langle \mathbf{a}, \mathbf{b} \rangle}{ || \mathbf{a} ||_2 \cdot ||\mathbf{b}||_2}\)
双塔模型的训练⚓︎
Pointwise 训练⚓︎
独立看待每个正样本、负样本,做简单的二元分类训练模型。正负样本组成一个数据集,在数据集上,每次取一个样本;随机梯度下降。
把召回看作二元分类任务:
- 对于正样本,鼓励 \(\cos (\mathbf{a}, \mathbf{b})\) 接近 1
- 对于负样本,鼓励 \(\cos (\mathbf{a}, \mathbf{b})\) 接近 -1
- 控制正负样本数量为 1: 2 或者 1:3;
Pairwise 训练⚓︎
每次取一个正样本、一个负样本;损失函数:Triplet Hinge/Logistics Loss;
输入是一个三元组,一个用户和2个物品 (用户、物品正样本、物品负样本;),特征做变换,记为 \((\mathbf{b}^+, \mathbf{b}^-, \mathbf{a})\);输入神经网络;正负样本共享神经网络参数,用户用单独的神经网络;训练后分别计算用户对两类物品的余弦相似度 : \(\cos (\mathbf{a}, \mathbf{b}^+)\), \(\cos (\mathbf{a}, \mathbf{b}^-)\) ;
- 基本想法:
-
用户对正样本的兴趣(相似度)尽可能大;而负样本的相似度尽可能小;
也就是 \(\cos (\mathbf{a}, \mathbf{b}^+)\) > \(\cos (\mathbf{a}, \mathbf{b}^-)\)。
处理损失函数的时候,就认定如果 \(\cos (\mathbf{a}, \mathbf{b}^+) > \cos (\mathbf{a}, \mathbf{b}^-) + m\),则没有损失;这里的 \(m\) 是超参数。需要调。
否则,损失等于 \(\cos (\mathbf{a}, \mathbf{b}^-) + m -\cos (\mathbf{a}, \mathbf{b}^+)\)
我们的损失函数就是: \(L(\mathbf{a}, \mathbf{b}^+, \mathbf{b}^-) = \max \{ 0, \cos (\mathbf{a}, \mathbf{b}^-) + m -\cos (\mathbf{a}, \mathbf{b}^+) \}\);这就是
Triplet Hinge Loss;也可以写作
Triplet Logistics Loss: \(\log (1 + \exp [ \sigma \cdot( \cos (\mathbf{a}, \mathbf{b}^-) -\cos (\mathbf{a}, \mathbf{b}^+))])\)这里的 \(\sigma\) 需要手动输入。
Listwise 训练⚓︎
每次选择一个正样本和多个负样本组成List,训练方式类似多元分类;
一条数据包含:
- 一个用户,特征向量: \(\mathbf{a}\)
- 一个正样本,特征向量: \(\mathbf{b}^+\)
- 多个负样本,特征向量: \(\mathbf{b}_{i}^-, (i = 1,...,n)\)
鼓励 \(\cos (\mathbf{a}, \mathbf{b}^+)\) 尽可能大; \(\cos (\mathbf{a}, \mathbf{b}_i^-)\) 尽可能小。
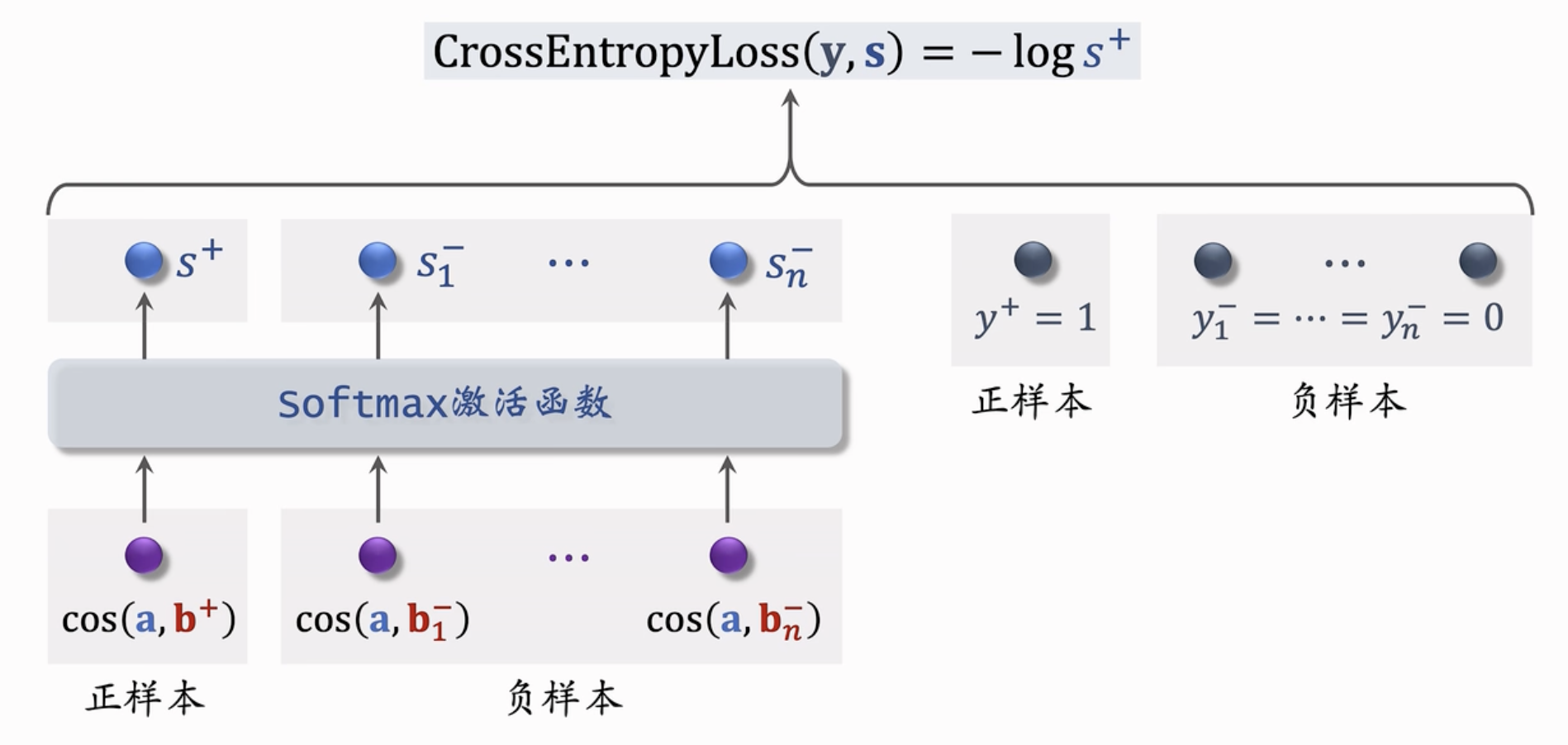
把在正负样本的相似度输入softmax激活函数,得到 \(n + 1\) 个分数,\(s^+, s^-_1, ... s^-_n\)。 我们希望正样本的分数接近1,而负样本(n个)的分数接近 0。我们设置 \(y^+ = 1\),设置负样本 \(y^-_1, y^-_2, ... = 0\)。目标函数就是 \(\mathbf{s}\) 和 \(\mathbf{y}\) 的交叉熵。 \(\text{CrossEnrtopyLoss}( y, s) = - \log s^+\)。
正负样本的选择⚓︎
- 正样本
- 用户点击过的物品(感兴趣);
- 负样本
- 没有被召回的样本 / 召回了但是被粗排、精排淘汰的 / 曝光但是没有被点击的。
一种不适用于召回的模型⚓︎
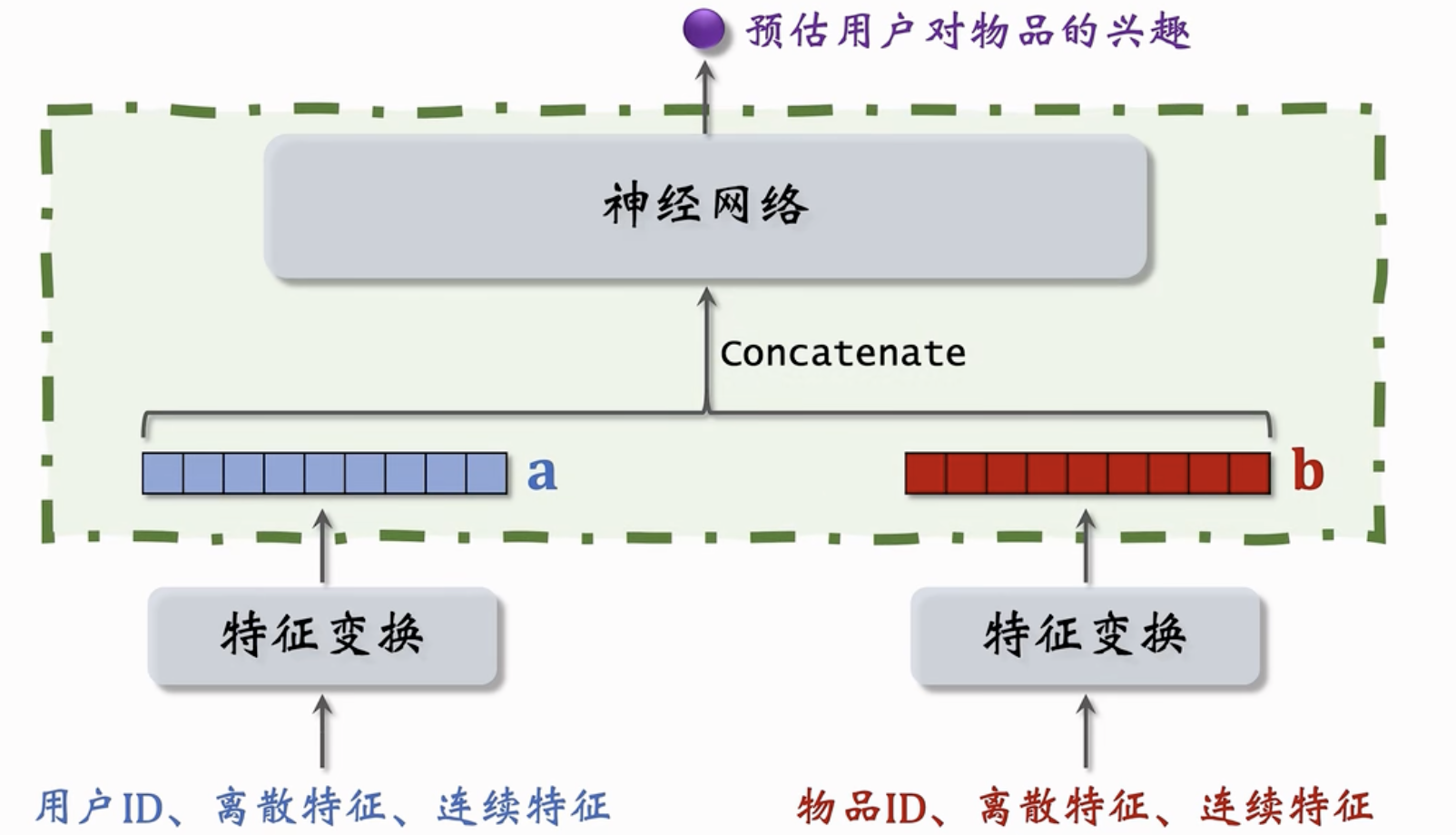
前期融合(在进入全连接层之前就把特征向量拼起来了,这种nn结构必须把所有用户的特征都输入模型,预估用户对所有物品的兴趣,没法用近似最近邻查找来寻找)和后期融合(只进入了一个用户的特征向量)的区别。这种神经网络输入一个实数,表示用户对物品的兴趣;双塔模型只会针对用户的所有特征concatenate,不会把用户和物品的特征concatenate;如果对物品+用户的特征做了concatenate,用来预估用户对物品的兴趣,那么不是用于召回的。而用于精排(排序)的。
近似最近邻查找用在什么地方?(线上计算的时候查找)
优点
矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\) 是独立训练的。很容易扩展到大规模(用户和物品)的场景下;每次训练的时候筛选正负样品即可。
Lecture 10. 正负样本的选择⚓︎
正样本⚓︎
- 正样本:曝光且有点击的用户-物品二元组。
-
问题:少部分物品占据大多数点击。 正样本大多是热门物品。
- 简单负样本:全体内做随机抽样
- 绝大多数样本用户都不会点击。因此随机抽,抽出的大概率就是负样本了。
- 简单负样本:Batch内负样本
-
选定用户-物品的二元组,正样本就是用户点击的,而同一个batch里第一个用户没有点击的就作为负样本。
缺点:一个样本出现在batch内的概率正比于点击次数。物品成为负样本的概率本该正比于点击次数的 3/4 次方,但这里正比于点击次数了。热门物品成为负样本的概率过大。
优化方法:记物品 \(i\) 被抽样到的概率 \(p_i\);预估用户对物品的兴趣: \(\cos (\mathbf{a}, \mathbf{b_i})\);训练的时候,调整为 \(\cos (\mathbf{a}, \mathbf{b_i}) - \log p_i\)
- 困难负样本
-
比如被粗排淘汰的物品、被排序淘汰的物品等。
一般训练数据时候会混合多种负样本,比如 50% 是全体物品(简单负样本),50%是没有通过排序的物品。
- 常见错误
-
❌:把曝光了但是没有点击的物品作为负样本。
因为我们的任务是找到那些用户感兴趣的和不感兴趣的(召回的目的),而不是那些比较感兴趣的和十分感兴趣的:这部分物品可能只是用户恰好没有点击,既然已经曝光了(经过精排重排),那么它已经很符合用户兴趣了,因此仅仅适合在训练排序模型的时候使用。
Lecture 11. 双塔模型的线上召回和更新⚓︎
双塔模型:用户塔和物品塔。物品塔存储物品的离散特征、连续特征;用户塔包含用户ID等特征。考虑物品很多(几亿个),因此需要离线存储:完成训练后,用物品塔计算物品向量直接存储在向量数据库中。
用户塔则是在用户发起推荐请求时,调用神经网络在线上现算一个用户向量,然后在线上做近似最近邻查找,返回相似度最高的 \(k\) 个物品。
为什么这么做
-
因为物品很多,每一次召回都需要1个用户向量和几亿个物品向量,太多了;
-
用户的兴趣点是动态变化的,而物品的特征相对稳定,短期内不会变化。
- 全量更新:在今天凌晨,用昨天全天的数据训练模型
-
- 一定要在昨天的模型基础上进行训练,不是随机初始化;
- 只做 1 epoch. 每天数据只用一遍;
- 发布新的用户塔神经网络和物品向量,供线上召回使用;
- 全量更新对数据流要求较低,可以延迟;
- 增量更新:用Online-learning更新模型参数
-
动机:用户的兴趣随时会发生变化,需要随时捕捉用户的兴趣。
- 需要搜集实时数据,从早到晚实时处理TFRecord文件。
- Online Learning,只更新用户ID Embedding,全联接层的参数是锁住的:只在全量更新的时候使用;
- 发布用户Embedding,供用户塔在线上计算用户向量。
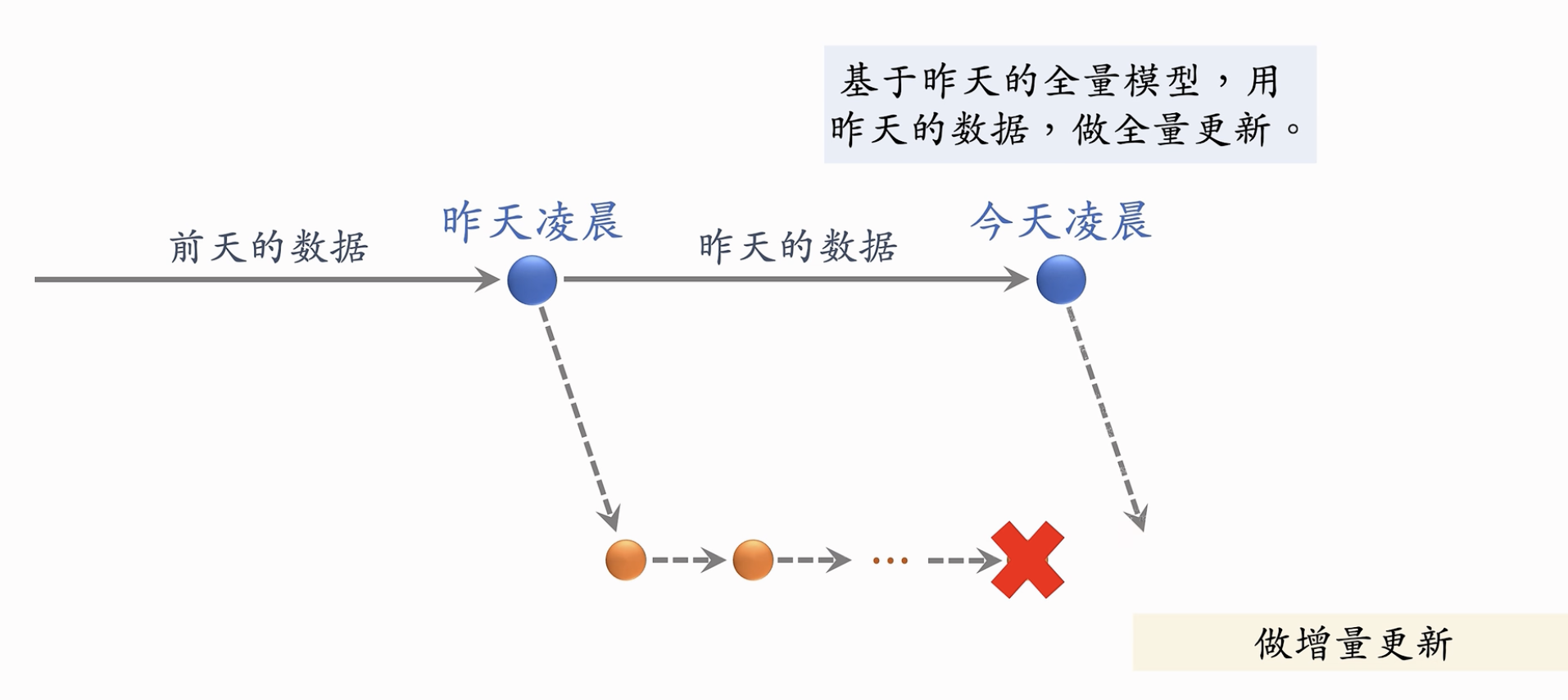
能不能只做增量更新不做全量更新呢?
❌。因为小时/分钟级别的数据是有偏的,表现会随着时段有波动,与全天数据的统计差距很大;同时,全量更新会Random Shuffle每天的数据,而增量是按顺序进行 1 epoch 训练的,全量的效果更好。
Lecture 12. 物品塔的自监督学习⚓︎
动机:物品塔学不好低曝光物品的向量表征。因为几乎所有推荐系统都存在少部分物品占据大部分曝光的情况,长尾效应严重。
对物品做多种随机特征变换,得到多种特征向量。相同物品在两种特征变换下的特征向量 \(\mathbf{b_i^{'}} 和 \mathbf{b_i^{''}}\) 应该有较高的相似度,而不同 物品的特征向量应该有较低的相似度。
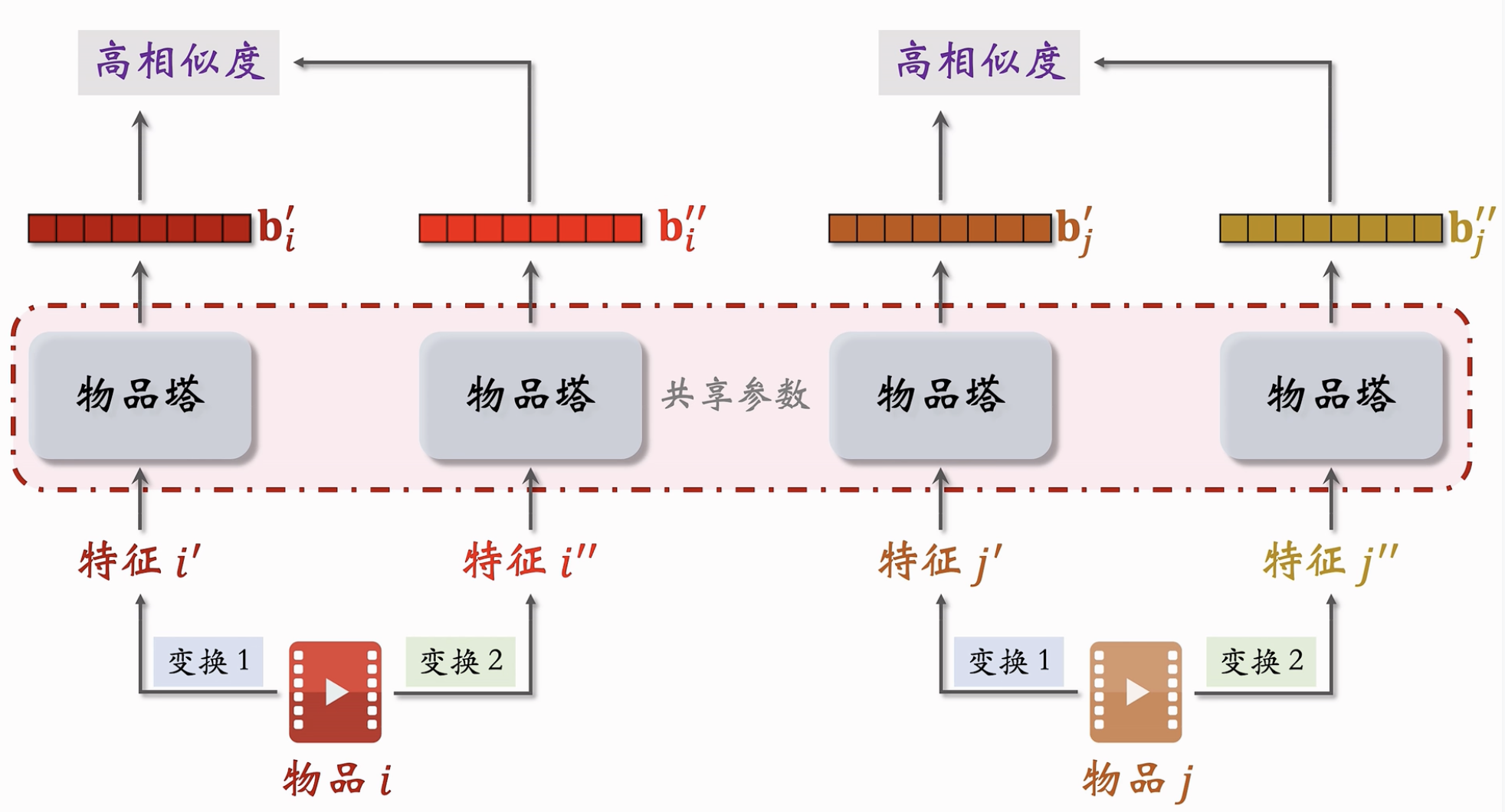
几种随机特征变换的方法:
- Random Mask
- 随机选择一些离散特征,把他们遮住;比如,类目:{数码、摄影},正常情况下会对两个类目做embedding,得到两个向量,最终加和/平均,得到最终的embedding,而现在,我们丢掉所有的类目,只保留default。
- Dropout(仅对多值离散特征生效)
- 一个物品可以有多个类目,那么我们随机选择50%的类目进行丢弃。比如一个物品有 {美妆、摄影},我们就Dropout一个,保留下另一个,比如 {美妆}。
- Complementary(互补特征)
- 把特征随机分成两组,每次保留一半的特征输入向量做embedding。比如:一共四个特征: {ID, 类目,关键词,城市},分成两组:{ID,关键词},和 {类目、城市}。我们选择{ID,关键词,Default,Default},相当于对这个物品仅仅保留2个特征,剩下的不保留,另一种也就是{Default,Default,类目,城市}。
- Mask 关联特征
-
把模型中一组关联的特征全部遮住。比如女性-美妆,就是互相关联的。
细节: xxx (2h:29min)
模型训练
- 损失函数
- ??
Lecture xx. 视频播放的建模⚓︎
除了前述的指标外,还有播放时长、完播率。如果用户看完了但是没有点赞转发,那么依然可以表示用户感兴趣。
- 播放时长的建模
-
直接用回归拟合播放时长效果不好,建议用 YouTube 的时长建模。
把统计特征(用户、视频、统计、场景)输入神经网络,输出经过多个全连接层。每个全连接层对应一个目标。对于统计观看时长的全连接层,把输出的结果记为 \(z\). 计算 \(p = \dfrac{\exp(z)}{ (1 + \exp(z)) }\)。
训练中要使用 \(p\) 拟合 \(y = t / (1 + t)\),损失函数是 \(p\) 和 \(y\) 的交叉熵,如果预估准确,那么 \(t\) (实际观看时长)就和 \(\exp(z)\) 是一样的. 线上推理的时候,就用 \(\exp(z)\) 作为播放时长的预估。最终作为融分公式的一项,参与视频播放排序。
- 视频完播的建模
-
例如,10 min 视频 4 min用户就关掉了。完播率 \(y = 0.4\).
让预估播放率 \(p\) 拟合 \(y\)(实际完播率)
\[Loss = y \log p + (1 - y) \log(1 - p)\]
把 \(p\) 作为影响融分公式的一项。
- 二元分类
定义完播指标:比如完播 x% 算作positive样本,其他negative样本。进行二元分类模型。线上预估完播率 p = 0.73, 则 P(播放 > 80%) = 0.73
实践中不能把完播率用到融分公式中(对长视频不公平)。需要拟合完播率-时长曲线,对线上预估的完播率进行调整:
p_finish = 预估完播率 / f(视频长度)
作为融分公式中的一项。进行分数融合。
Lectire xx. 排序模型的特征⚓︎
每个用户都有用户属性,记录在用户画像中。(User Profile)
- 用户ID(在召回、排序中embedding)
- 人口统计学属性:性别、年龄
- 账号信息:活跃度、新老;
- 感兴趣的类目、品牌
物品画像(Item Profile)
- 物品ID(在召回、排序中embedding)
- 发布时间
- GeoHash(经纬度编码)
- 类目、品牌
- 字数、图片数、视频清晰度
- 内容信息量、图片质量(事先先用人工标注数据训练CV/NLP),视频发布时候进行打分
用户统计特征: