机器学习中常用的一些评价指标：AUC, ROC, F1 Score ...⚓︎

约 3769 个字 264 行代码 3 张图片预计阅读时间 16 分钟

Confusion Matrix （混淆矩阵）⚓︎

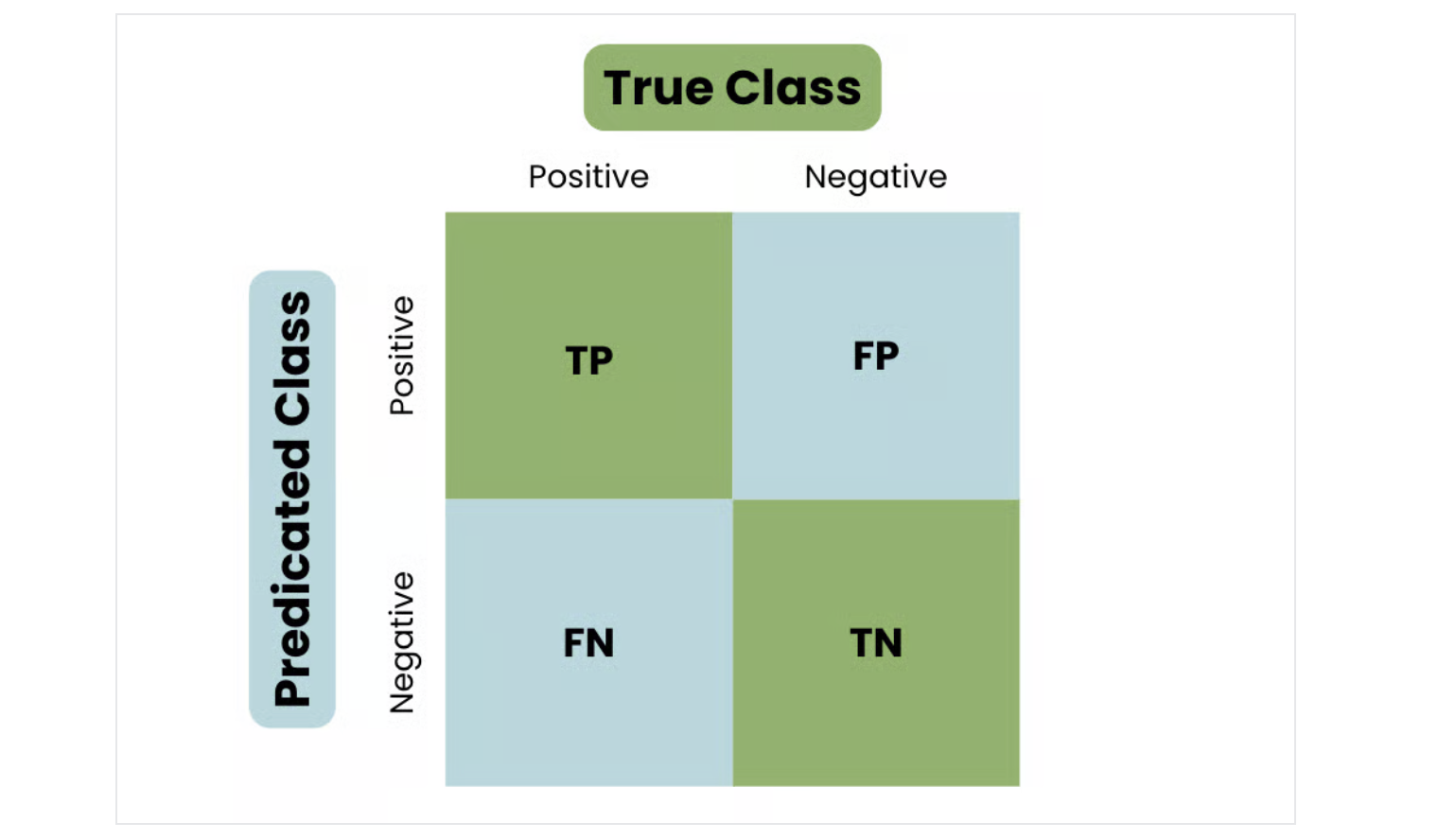
我们需要一种工具总结某种机器学习方法在测试集上的效果。此时我们可以引入混淆矩阵（Confusion Matrix）。对于一个二分类问题，很明显有如下4种情况：

原本是Postive，预测为 Positive；（True Positive）
原本是Negative，预测为 Negative；（True Negative）
原本是Positive，但预测为 Negative；（False Negative）
原本是Negative，但预测为 Positive；（False Positive）

一种记忆方法是，上述所有的Positive 和 Negative 都是“预测的结果”。因此，只有当预测和实际是一样的时候，才是 True ~ ，否则是 False ~ ...

我们可以绘制出如下的图：

举个例子：我们用下表来展示Algo1 / Algo2 两种算法的分类效果：

Algo1	Act. Positive	Act. Negative	Algo2	Act. Positive	Act. Negative
Pred. Positive	142	22	Pred. Positive	139	20
Pred. Negative	29	110	Pred. Negative	32	112

拓展一下。如果我们不是一个二分类问题，而是一个多分类问题，比如我们需要预测某个Item被分在哪个类中，那么，有\(N\)个类，就有 \(N \times N\) 大小的混淆矩阵，其中的主对角线上表示分类正确的数目。

Accuracy, Recall, Precision ...⚓︎

一个显而易见的事情是，我们想知道算法到底分对了多少样本，也就是，对于所有样本，有多少样本本身是Positive，分成Positive，或者本身是Negative，分成了Negative。于是我们有：

\[\dfrac{TP + TN}{TP + FP + TN + FN}\]

这就是准确率（Accuracy）。

现在，我们希望知道，有多少原本就是 Positive 的样本，正确地分类为了 Positive(Correctly classified)了，也就是从 Positive的样本视角看，分类器筛出了多少的比例。即：

\[\dfrac{TP}{TP + FN}\]

这就是“True Positive Rate”，真阳性率，也叫召回率（Recall）。

同样地，我们也希望知道，对于原本就是 Negative 的样本，有多少被错误地分为了 Positive，也就是假阳性率 （False Positive Rate）：

\[\dfrac{FP}{FP + TN}\]

上面2点都是从样本角度出发进行划分的，我们也可以从预测算法的角度为判断依据进行划分。比如，我们想知道预测为 Positive 的样本中，有多少实际就是 Positive的，也就是：

\[\dfrac{TP}{TP + FP}\]

这个指标就是 Precision （查准率）。

ROC⚓︎

ROC曲线（Receiver Operating Characteristic Curve） 是一种用于评估==二分类模型==性能的可视化工具。它通过展示不同分类阈值下模型的 真阳性率（TPR） 和 假阳性率（FPR） 之间的权衡关系，帮助理解模型对正负样本的区分能力。

横轴（FPR）：假阳性率（False Positive Rate），即负样本中被错误预测为正样本的比例，计算公式为：

\[FPR = \frac{FP}{FP + TN}\]

纵轴（TPR）：真阳性率（True Positive Rate），即正样本中被正确预测的比例，等价于召回率（Recall），计算公式为：

\[TPR = \frac{TP}{TP + FN}\]

我们知道，以逻辑回归为例，模型通常输出样本属于正类的概率，也就是说，我们可以认为，概率 > 50%的，就是正样本，我们也可以认为，概率 > 60 % 的就是正样本，这里的 50%, 60% 就是一个阈值。对于同一个测试集，选择不同的阈值，你可以生成不同的预测结果，而对于你生成的每一个预测结果，你都可以对应计算出这个结果的真 or 假阳性率。

对每个阈值，计算对应的TPR和FPR，形成ROC曲线上的一个点。此时我们再连接所有点连成曲线，即为ROC曲线。

解读

对角线（AUC=0.5）：表示模型无区分能力（相当于随机猜测）。
左上角（AUC=1）：理想模型，所有正样本的预测概率均高于负样本。
曲线位置：曲线越靠近左上角，模型性能越好。

如何画ROC曲线⚓︎

怎么画这个图呢？

第一个问题无疑是咱们应该怎么取那个阈值。一个简单的做法是根据我们在测试集上所有输出的概率来取。若模型对3个样本的预测概率为 [0.2, 0.8, 0.6]，候选阈值为 [0.2, 0.8, 0.6]。额外补充阈值 0.0（所有样本均判为正类）和 1.0（所有样本均判为负类）作为起点和终点并把前面的阈值升序排一下，就可以了，我们的阈值就是 [0, 0.2, 0.6, 0.8, 1.0]

第二个问题无疑是怎么调整这个阈值。我们让阈值从 1.0 逐步降低到 0.0 即可。此时 TPR（真阳性率） 逐步上升（正样本被正确分类的比例提高）。FPR（假阳性率） 也逐步上升（负样本被误判的比例提高）。

快速看看AUC曲线长啥样！

import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, roc_auc_score, RocCurveDisplay,  precision_recall_curve
import matplotlib.pyplot as plt

X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

clf = LogisticRegression()  # Logistics Regression Classifier
clf.fit(X_train, y_train)   # X_train and y_train for training
y_score = clf.predict_proba(X_test)[:, 1]  # Predict on x_test
fpr, tpr, thresholds = roc_curve(y_test, y_score)
auc_score = roc_auc_score(y_test, y_score)
display = RocCurveDisplay(fpr=fpr, tpr=tpr, roc_auc=auc_score,
                                estimator_name='example estimator')
display.plot()
plt.plot([0, 1], [0, 1], linestyle='--', color='r', label='Random Classifier')  
plt.show()

一般而言，AUC曲线是呈阶梯状增加的，也就是在相邻两点之间，若FPR或TPR发生变化，则通过线性插值连接。最终曲线呈“阶梯状”，反映阈值调整时分类结果的离散跳跃。

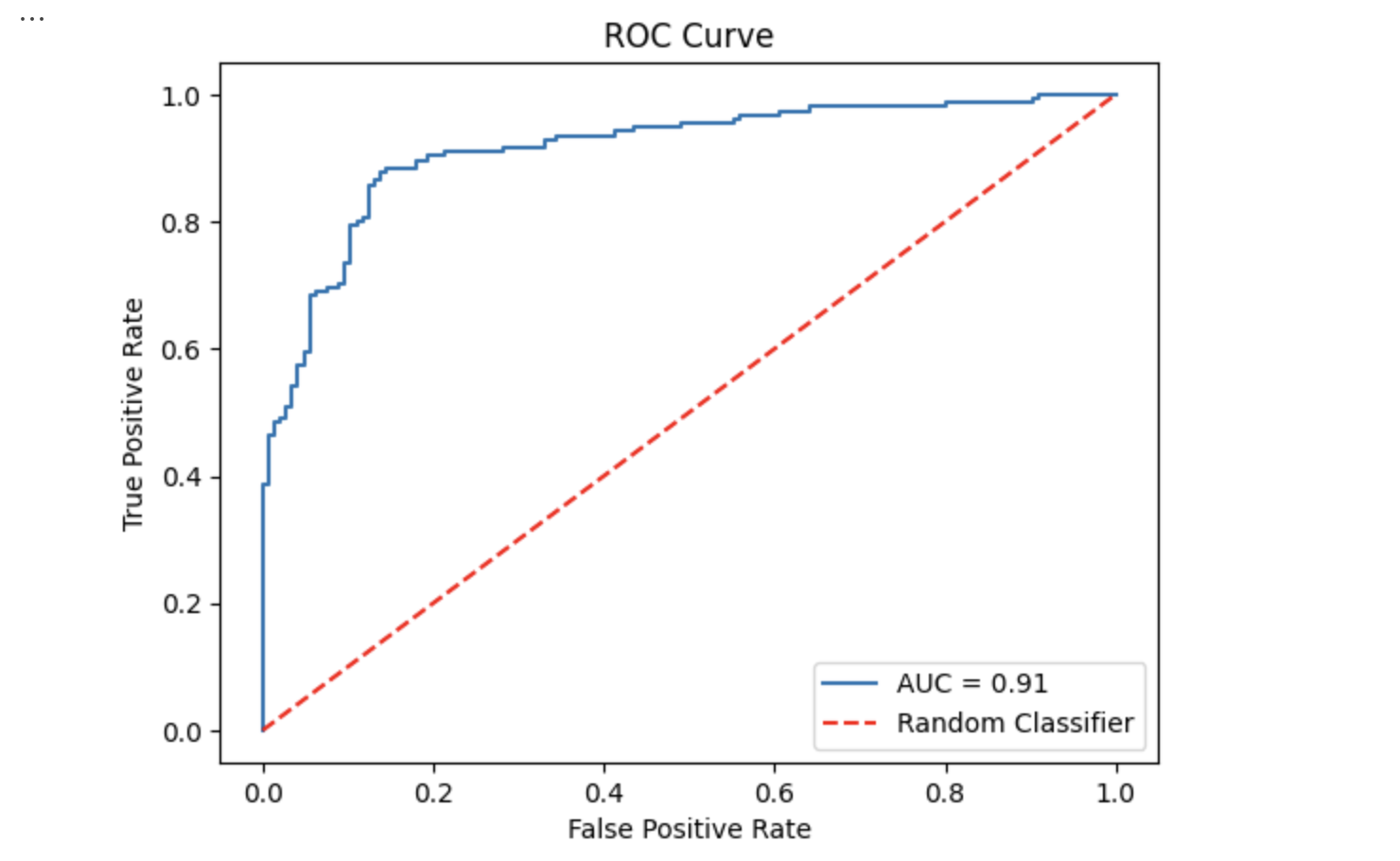
为什么会出现这样的图像呢？

我们可以验证一下，比如我们取出上面所有的预测概率值并且从大到小排序。我们基于这些概率分别计算 TPR， FPR。手撕代码如下：

def manual_tpr_fpr(y_true, y_pred_prob, threshold):
    y_pred = np.where(y_pred_prob >= threshold, 1, 0)
    # Get TP, FP, TN, FN
    tp = np.sum((y_pred == 1) & (y_true == 1))
    fp = np.sum((y_pred == 1) & (y_true == 0))
    tn = np.sum((y_pred == 0) & (y_true == 0))
    fn = np.sum((y_pred == 0) & (y_true == 1))

    # Get TPR, FPR ... 
    tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
    fpr = fp / (fp + tn) if (fp + tn) > 0 else 0.0

    return tpr, fpr

y_true = y_test
for threshold in threshold_np:
    tpr, fpr = manual_tpr_fpr(y_true, y_score, threshold)
    print(round(threshold,6), round(tpr, 6), round(fpr, 6))

其中，第一列对应阈值概率，第二列对应TPR，第三列对应FPR。结果类似：

0.999903 0.006452 0.0
0.999679 0.012903 0.0
0.999622 0.019355 0.0
0.999499 0.025806 0.0
0.999479 0.032258 0.0
0.998925 0.03871 0.0
......
......
0.018623 0.987097 0.834483
0.018358 0.987097 0.841379
0.016268 0.987097 0.848276
0.016144 0.987097 0.855172
0.015737 0.987097 0.862069

什么意思呢，就是，不同的阈值可能对应了不同TPR，但是相同FPR，或者同一个TPR，但是不同FPR。对于第一种情况，就类似于这段图像是一个竖直的线，对第二种情况，对应这段图像是一个水平线。 这种情况是因为某些相邻阈值会导致相同的 TPR/FPR，两个阈值之间无样本被重新分类。正是这么多细小的线水平竖直连接起来，就构成了这么一个阶梯形状的图像。

AUC⚓︎

二分类下的 AUC⚓︎

ROC曲线本身的含义还可以进一步被挖掘。比如，我们可以计算出ROC曲线下的面积。这个值对应的是，若随机抽取一个阳性样本和一个阴性样本，分类器判断阳性样本的值高于阴性样本的概率。

或者，是模型正确排序一对正负样本的概率。

如果模型对正样本的预测概率为0.8，对负样本的预测概率为0.3，则模型正确排序了这两个样本。反之，如果两个样本一个 0.7, 一个 0.8，那么它并没有正确排序这两个样本。

现在，一个重要的问题来了，如何计算AUC？和ROC不同，AUC是一个值。

我们可通过梯形法则（Trapezoidal Rule）近似计算离散点的积分，也就是对阈值从高到低排序后计算每个阈值对应的FPR，TPR，然后：

\[AUC = \sum^n_{i = 1} \dfrac{(FPR_i - FPR_{i-1}) \times (TPR_i + TPR_{i - 1})}{2}\]

注意，AUC反映模型对正负样本的排序能力，与样本数量无关。

我们可以把完整的代码搓出来：

def manual_tpr_fpr(y_true, y_pred_prob, threshold):

    y_pred = np.where(y_pred_prob >= threshold, 1, 0)

    # Get TP, FP, TN, FN
    tp = np.sum((y_pred == 1) & (y_true == 1))
    fp = np.sum((y_pred == 1) & (y_true == 0))
    tn = np.sum((y_pred == 0) & (y_true == 0))
    fn = np.sum((y_pred == 0) & (y_true == 1))

    # Get TPR, FPR ... 
    tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
    fpr = fp / (fp + tn) if (fp + tn) > 0 else 0.0

    return tpr, fpr

if __name__ == "__main__":
    threshold_np = sorted(y_score.tolist(), reverse = True)
    y_true = y_test
    auc_score_manual = 0
    prev_tpr = 0; prev_fpr = 0
    for idx, threshold in enumerate(threshold_np):
        tpr, fpr = manual_tpr_fpr(y_true, y_score, threshold)
        # print(round(threshold,6), round(tpr, 6), round(fpr, 6))
        if idx > 0:
            auc_score_manual += (fpr - prev_fpr) * (tpr + prev_tpr) / 2
        prev_tpr, prev_fpr = tpr, fpr 
    print(f"Manual Check AUC: {auc_score_manual}")
    # Is the same as above!

多分类下的AUC⚓︎

多分类的 AUC 没有单一的标准定义，但一般常用的方法有以下几种：

(1) One-vs-Rest (OvR): 方法：将每个类别视为正类，其他所有类别视为负类，分别计算每个类别的二分类 AUC，然后取平均（宏平均或微平均）。

\[\text{AUC}_{\text{macro-ovr}} = \frac{1}{C} \sum_{i=1}^C \text{AUC}_i\]

其中 \(C\) 是类别数，\(\text{AUC}_i\) 是第 \(i\) 类的二分类 AUC。

(2) One-vs-One (OvO): 方法：对每两个类别组合计算二分类 AUC，然后取所有组合的平均。这里的“每两个类别”，意思是取出预测结果与真实结果里结果为 \(i, j\) 的所有样本求AUC，如果一个样本，真实类别不属于 \(i\) 或者 \(j\)，同时预测结果也不属于 \(i\) 或者 \(j\)，那么不参与 AUC 计算。

\[\text{AUC}_{\text{macro-ovo}} = \frac{2}{C(C-1)} \sum_{i=1}^{C-1} \sum_{j=i+1}^C \text{AUC}_{ij}\]

其中 \(\text{AUC}_{ij}\) 是类别 \(i\) 和 \(j\) 的二分类 AUC。

我们可以手动实现这两种指标的计算方式，并且和 sklearn 给出的结果进行比较。证明是一致的。实际不需要这么麻烦，roc_auc_score 就可以了。

强调一下，要计算AUC，输入就必须包含

每一个样本的真实类别；
每一个样本预测算法给出的不同类别的概率；

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score
import numpy as np

# 加载数据
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 训练模型（需支持概率预测）
model = RandomForestClassifier()
model.fit(X_train, y_train)

# 获取预测概率（形状为 [n_samples, n_classes]）
y_proba = model.predict_proba(X_test)

np.random.seed(2025)
test_y_proba = np.random.rand(y_test.shape[0], 3)

# 逐行归一化（确保每行和为1）
test_y_proba_norm = test_y_proba / test_y_proba.sum(axis=1, keepdims=True)

# 验证结果

# One-vs-Rest 宏平均
auc_ovr_macro = roc_auc_score(
    y_test, test_y_proba_norm, multi_class='ovr', average='macro'
)

# One-vs-One 加权平均
auc_ovo_weighted = roc_auc_score(
    y_test, test_y_proba_norm, multi_class='ovo', average='macro'
)

print(f"Scikit Learn: Macro AUC (OvR): {auc_ovr_macro:.6f}")
print(f"Scikit Learn: Macro AUC (OvO): {auc_ovo_weighted:.6f}")
# 总结：多分类时候的AUC的计算：需要概率；
# 多分类时候F1 score的计算：只需要输出分类结果，不需要概率；


from itertools import combinations
def manual_tpr_fpr(y_true, y_pred_prob, threshold):

    y_pred = np.where(y_pred_prob >= threshold, 1, 0)
    # Get TP, FP, TN, FN
    tp = np.sum((y_pred == 1) & (y_true == 1))
    fp = np.sum((y_pred == 1) & (y_true == 0))
    tn = np.sum((y_pred == 0) & (y_true == 0))
    fn = np.sum((y_pred == 0) & (y_true == 1))

    # Get TPR, FPR ... 
    tpr = tp / (tp + fn) if (tp + fn) > 0 else 0.0
    fpr = fp / (fp + tn) if (fp + tn) > 0 else 0.0

    return tpr, fpr

def manual_auc_binary(y_true, y_score):
    threshold_np = sorted(y_score.tolist(), reverse = True)
    prev_tpr = 0; prev_fpr = 0; auc_score_manual = 0
    for idx, threshold in enumerate(threshold_np):
        tpr, fpr = manual_tpr_fpr(y_true, y_score, threshold)
        if idx > 0:
            auc_score_manual += (fpr - prev_fpr) * (tpr + prev_tpr) / 2
        prev_tpr, prev_fpr = tpr, fpr 
    return auc_score_manual


def manual_auc_multi_class(y_test, y_score, multi_class = "ovr"):
    labels = np.unique(y_test)
    res = []
    if multi_class == "ovo":
        # OvO means One. VS. One, 
        label_combs = list(combinations(labels, 2))
        for label_comb in label_combs:

            label_a, label_b = label_comb[0], label_comb[1] 
            a_mask = y_test == label_a
            b_mask = y_test == label_b
            ab_mask = np.logical_or(a_mask, b_mask)

            a_true = a_mask[ab_mask]
            b_true = b_mask[ab_mask]

            y_binary_a = np.where(y_test == label_a, 1, 0)[ab_mask]
            cur_score_a = y_score[:, label_a][ab_mask]
            cur_auc_a = manual_auc_binary(y_binary_a, cur_score_a)

            y_binary_b = np.where(y_test == label_b, 1, 0)[ab_mask]
            cur_score_b = y_score[:, label_b][ab_mask]
            cur_auc_b = manual_auc_binary(y_binary_b, cur_score_b)
            res.append((cur_auc_a + cur_auc_b) / 2)

        return sum(res) / len(label_combs)

    else:
        # By default perform "One. vs Rest."
        for idx, i in enumerate(labels):
            cur_score = y_score[:, i]
            y_test_binary = np.where(y_test == i, 1, 0)
            cur_auc = manual_auc_binary(y_test_binary, cur_score)
            res.append(cur_auc)
        return sum(res) / len(res)



if __name__ == "__main__":
    res = manual_auc_multi_class(y_test, test_y_proba_norm, "ovr")
    print("Manual AUC (OvR):", res)
    res = manual_auc_multi_class(y_test, test_y_proba_norm, "ovo")
    print("Manual AUC (OvO):", res)

PR-curve⚓︎

PR曲线 Precision-Recall Curve. 是另一种评估二分类模型性能的重要工具，尤其在类别不平衡场景下比ROC曲线更具参考价值。

绘制 PR curve⚓︎

横轴（Recall）：召回率（真阳性率），计算公式为：

\[TPR = \frac{TP}{TP + FN}\]

纵轴（Precision）：精确率，计算公式为：

\[Precision = \frac{TP}{TP + FP}\]

注意，在ROC中TPR是纵轴，但是在PR curve中，是横轴。

绘制步骤和ROC曲线是类似的：

将预测概率从高到低排序。
依次将每个概率作为阈值，计算对应的Precision和Recall。
连接所有点形成PR曲线。

怎么理解

曲线形状：呈下降趋势（阈值降低时，Recall上升，但Precision可能下降）。
关键点：
右上角（Recall=1, Precision=正样本比例）：所有样本均判为正类。
左上角（Precision=1, Recall=0）：无样本判为正类。

PR曲线的作用

类别不平衡场景的敏感性：当负样本远多于正样本时（如欺诈检测中99%为正常交易），ROC曲线的FPR可能被稀释（分母FP+TN过大），导致评估失真。而，Precision关注预测为正类的准确性（即“判为正类的样本中有多少是真的正类”）。

Recall (TPR) 关注正样本的覆盖率（即“真实正类中有多少被正确识别”）。两者均聚焦正样本，对类别分布不敏感。

举个例子，应用在召回正样本时，误判负样本的比例较低（高Precision）。适用于需要减少误报的场景（如垃圾邮件过滤、医学诊断）。

试试看！还是先前的代码，但是调个包！Give it a shot!

from sklearn.metrics import PrecisionRecallDisplay
display = PrecisionRecallDisplay.from_estimator(
    clf, X_test, y_test, name="LogisticsRegression", plot_chance_level=True,
)
_ = display.ax_.set_title("2-class Precision-Recall curve")
plt.show()

Then you got:

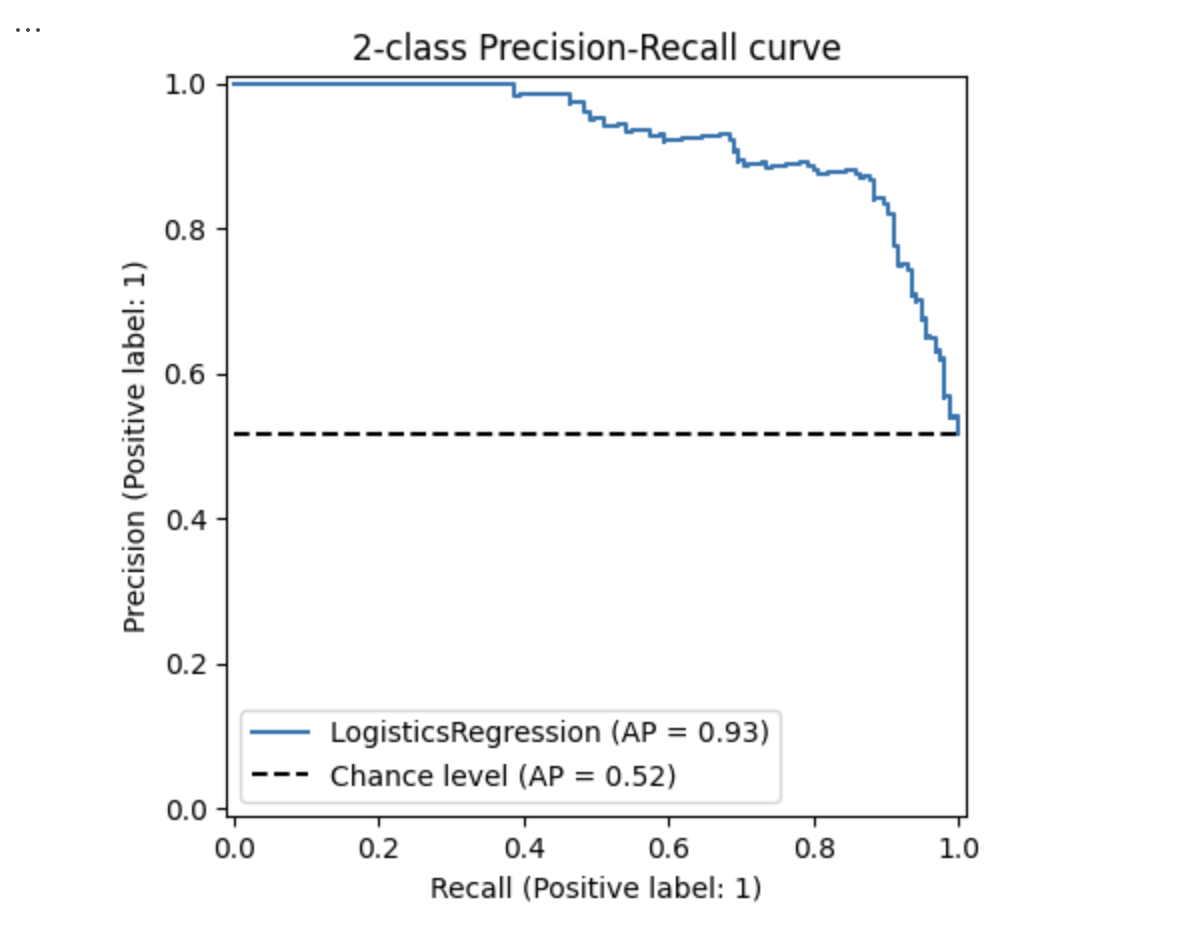
此时你会发现，sklearn帮你算好了一个叫AP (Average Precision)的指标。实际上这个可以近似理解为PR-AUC，也就是这个曲线下的面积，用于量化模型在不同召回率（Recall）下的平均精确率（Precision）。其一般计算公式：

\[AP = \sum_{k=1}^{N} Precision(k) \cdot \Delta Recall(k)\]

必须说一下，sklearn 中的 average_precision_score 计算并不是直接使用梯形法则（基于插值），因为 “梯形规则使用线性插值，可能过于乐观。” (is different from computing the area under the precision-recall curve with the trapezoidal rule, which uses linear interpolation and can be too optimistic.) 因此如果你直接计算梯形面积会发现和那个值对不上。

from sklearn.metrics import average_precision_score

ap = average_precision_score(y_test, y_score)
print(f"AP = {ap:.6f}")  
ap_maunal = 0
for i, precision in enumerate(precisions):
    if i > 0:
        ap_maunal += abs(- recalls[i] + recalls[i - 1]) * precision
print(f"Maunal Check: {ap_maunal}")

结论

AP > 随机基线 → 模型有效。

AP越接近1 → 模型性能越接近完美（所有正样本预测概率高于负样本）。

罗列一下PR曲线下的AUC和ROC曲线下的区别与联系：

指标	关注点	适用场景	基线值
AP	正样本的预测准确性	类别不平衡（正样本稀少）	正样本比例（如0.52）
AUC-ROC	正负样本的全局排序能力	类别均衡或需全局排序能力的任务	0.5（随机猜测）

一个简单的例子是，在医学检测中，阳性样本本身不多（正样本占比1%），若模型AP=0.8（基线AP=0.01），说明模型显著优于随机；而ROC-AUC=0.9可能因类别不平衡掩盖问题。

F1 Score⚓︎

F1 Score 是 精确率（Precision） 和 召回率（Recall） 的调和平均数，直接通过公式计算得出：

\[\text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]

相比于前面提到的AUC，你可以观察到，它所需要的不是预测概率，而是给定某个阈值下的预测结果，计算预测结果的Precision和Recall就能直接得到了。

何时使用 F1 Score？何时使用 AUC？

使用 F1 Score 的场景

需要快速评估模型的分类性能。
明确关注精确率和召回率的平衡（如医疗诊断、欺诈检测）。
需要确保正类样本的识别能力。

使用 ROC/AUC 的场景

需要评估模型的概率预测质量（如广告点击率预估）。
关注模型的整体排序能力（如推荐系统的物品排序）。
在类别不平衡但希望指标对阈值选择不敏感时。

这里还需要补充一个“宏平均”和“微平均”的概念。我们在提及多分类问题AUC这个指标的时候就已经提及了但没有展开。

在多分类问题中，宏平均（Macro-average）和微平均（Micro-average）是两种常用的指标汇总方式，用于将各类别的性能指标综合为一个全局值。以下是它们的核心区别、计算方法和适用场景的详细解释：

(1) 宏平均（Macro-average）

平等对待每个类别，无论其样本量大小。即：

分别计算每个类别的指标（如精确率、召回率、F1 Score）。
对所有类别的指标取算术平均。

\[\text{F1}_{\text{macro}} = \frac{1}{C} \sum_{i=1}^C \text{F1}_i\]

其中 \(C\) 是类别数，\(\text{F1}_i\) 是第 \(i\) 类的 F1 Score。

(2) 微平均（Micro-average）: 平等对待每个样本，所有类别的预测结果合并后计算全局指标。 1. 合并所有类别的 TP、FP、FN（例如，将多分类视为多个二分类的扩展）。 2. 基于合并后的统计量计算全局指标（即全局Precision和Recall）。

\[\text{Precision}_{\text{micro}} = \frac{\sum_{i=1}^C \text{TP}_i}{\sum_{i=1}^C (\text{TP}_i + \text{FP}_i)}\]

\[\text{Recall}_{\text{micro}} = \frac{\sum_{i=1}^C \text{TP}_i}{\sum_{i=1}^C (\text{TP}_i + \text{FN}_i)}\]

\[\text{F1}_{\text{micro}} = 2 \times \frac{\text{Precision}_{\text{micro}} \times \text{Recall}_{\text{micro}}}{\text{Precision}_{\text{micro}} + \text{Recall}_{\text{micro}}}\]

3. 核心区别 | 特性 | 宏平均 | 微平均 | | -------------------- | ------------------------------ | ------------------------------------ | | 权重逻辑 | 每个类别的权重相等 | 每个样本的权重相等 | | 计算方式 | 先计算各类别指标，再取平均 | 合并所有类别的统计量，再计算全局指标 | | 对类别不平衡的敏感度 | 更关注小类别的性能（平等对待） | 更关注大类别的性能（受样本量影响） | | 适用场景 | 类别重要性相同（如罕见病诊断） | 关注整体性能（如广告点击率预测） |

如何选择

选择宏平均：

每个类别的重要性相同（如医疗诊断中的不同疾病）。
数据存在类别不平衡，但需避免大类别主导结果。

选择微平均：

更关注整体预测准确性（如垃圾邮件分类）。
各类别样本量分布均匀，或大类别更重要。

把手弄脏：我们可以手动实现Macro/Micro F1 score的计算：

import numpy as np 
from sklearn.metrics import f1_score

def f1_score_macro(y_true, y_pred):
    labels = np.unique(np.concatenate([y_true, y_pred]))
    tmp_res = np.empty(labels.shape[0])
    for idx, i in enumerate(labels):
        tp = np.sum((y_pred == i) & (y_true == i))
        fp = np.sum((y_pred == i) & (y_true != i))
        tn = np.sum((y_pred != i) & (y_true != i))
        fn = np.sum((y_pred != i) & (y_true == i))
        precision = tp / (tp + fp) if tp + fp > 0 else 0.0
        recall = tp / (tp + fn) if tp + fn > 0 else 0.0
        tmp_res[idx] = 2 * precision * recall / max(precision + recall, 1e-5)
    return np.average(tmp_res)

def f1_score_micro(y_true, y_pred):
    labels = np.unique(np.concatenate([y_true, y_pred]))
    tps = []
    fps = []
    tns = []
    fns = []
    for i in labels:
        tp = np.sum((y_pred == i) & (y_true == i))
        fp = np.sum((y_pred == i) & (y_true != i))
        tn = np.sum((y_pred != i) & (y_true != i))
        fn = np.sum((y_pred != i) & (y_true == i))
        tps.append(tp)
        fps.append(fp)
        tns.append(tn)
        fns.append(fn)
    tps = np.array(tps); fps = np.array(fps); tns = np.array(tps); fns = np.array(fns)
    precision = np.sum(tps) / (np.sum(tps) + np.sum(fps))
    recall = np.sum(tps) / (np.sum(tps) + np.sum(fns))
    return 2 * precision * recall / (precision + recall)


if __name__ == "__main__":
    # 真实标签和预测标签（3个类别）
    y_true = np.array([0, 1, 2, 1, 2, 0, 1, 1, 0, 1, 2, 0, 1, 0, 2, 1, 0, 1, 2, 0, 0])
    y_pred = np.array([0, 2, 1, 0, 0, 1, 2, 1, 0, 0, 0, 1, 1, 2, 1, 1, 0, 2, 2, 0, 1])

    # 宏平均（Macro-F1）：各类别 F1 的简单平均
    macro_f1 = f1_score(y_true, y_pred, average="macro")

    # 微平均（Micro-F1）：全局 TP/FP/FN 计算的 F1
    micro_f1 = f1_score(y_true, y_pred, average="micro")

    print(f"Macro-F1: {macro_f1:.4f}") 
    print(f"Micro-F1: {micro_f1:.4f}") 
    print("Benchmark Above .... ")
    macro_res = f1_score_macro(y_true, y_pred)
    print(macro_res)
    micro_res = f1_score_micro(y_true, y_pred)
    print(micro_res)