决策树 ｜ 树模型

约 5412 个字 7 张图片 预计阅读时间 18 分钟 总阅读量 次

深入理解决策树 (Decision Tree) 模型

决策树是后续更复杂的集成模型（如随机森林、XGBoost）的基础，理解它至关重要。

解决的问题与作用

决策树 (Decision Tree) 是一种基本的监督学习算法，可用于分类和回归任务。

它试图解决的问题是：通过从数据中学习一系列简单的决策规则，来构建一个模型，用于预测目标变量的值。

• 作用/优点：
  1. 可解释性强：模型形式为树状结构，非常直观，易于向非技术人员解释。这种模型通常被称为“白盒模型”。
  2. 计算简单：预测阶段的计算成本很低。
  3. 数据预处理要求低：不需要对数据进行归一化或标准化。
  4. 能够处理混合类型数据：可以同时处理数值型和类别型特征。

算法流程

决策树的生成是一个递归构建的过程，遵循“分而治之”的策略。

1. 开始：所有训练数据都在根节点。
2. 特征选择：遍历当前节点中所有数据的每一个特征，选择一个最优切分特征和一个最优切分点。这个“最优”的标准是使得分裂后的子节点“纯度”最高（或者说不确定性最小）。
3. 分裂：根据最优特征和切分点，将当前节点的数据集划分为多个子集，每个子集构成一个新的子节点。
4. 递归：对每个子节点，递归地重复步骤 2 和 3。
5. 停止：递归在以下情况停止，当前节点成为叶子节点：
   • 当前节点的所有样本都属于同一个类别。
   • 没有剩余的特征可以用来进行划分。
   • 达到了预设的停止条件，如树的最大深度、节点最小样本数等（这是预剪枝策略）。

重要知识点（面试核心）

决策树的核心在于如何选择最优切分特征。历史上主要有三种经典算法，它们的主要区别就在于这个选择标准。

1. ID3 算法 -> 信息增益 (Information Gain)

   • 核心思想：选择一个特征进行分裂，使得分裂后的信息不确定性下降得最多。这种不确定性的下降程度就叫做“信息增益”。

   • 度量标准：熵 (Entropy)。熵用来度量一个数据集的纯度，熵越小，纯度越高。

     \[
     \text{Entropy}(D) = -\sum_{k=1}^{|\mathcal{Y}|} p_k \log_2(p_k)
     \]

     其中，\(D\) 是数据集，\(|\mathcal{Y}|\) 是类别总数，\(p_k\) 是第 \(k\) 类样本在数据集 \(D\) 中所占的比例。

     我们在每次分支的时候，都希望这个熵尽可能地小，这样，每一个分支都是尽可能地“Pure”（纯净）的。

   • 信息增益：分裂前的数据集熵，减去分裂后所有子节点熵的加权平均。 $$ \text{Gain}(D, A) = \text{Entropy}(D) - \sum_{v=1}^{V} \frac{|D^v|}{|D|} \text{Entropy}(D^v) $$

     其中，\(A\) 是用来分裂的特征，\(V\) 是特征 \(A\) 的取值个数，\(D^v\) 是 \(D\) 中在特征 \(A\) 上取值为 \(v\) 的样本子集。 * 缺点：信息增益偏爱取值较多的特征。一个特征的取值越多，分裂出的子节点就越多、越“纯”，算出来的增益就越大。极端情况下，如果一个特征对每个样本都有唯一的值（如学号ID），那么它的信息增益最大，但这显然是无用的。

在选择一个特征进行分支后，我们希望所有子节点的加权平均熵尽可能小

一个节点的熵代表了这个节点数据的不确定性或“不纯度”。

• 熵最大 (最不纯)：当一个节点中，各个类别的样本数量完全相等时，熵达到最大值。例如，一个节点有50个正样本和50个负样本，此时我们完全无法判断这个节点的倾向，不确定性最高。
• 熵最小 (最纯)：当一个节点中，所有样本都属于同一个类别时，熵为0。例如，一个节点有100个正样本和0个负样本，此时没有任何不确定性，这个节点已经是“纯”的。

因此，决策树的目标就是，通过一次分裂，将一个“不纯的”父节点，分裂成多个“尽可能纯的”子节点。

如果两个新分出的支，每一支都有较多的类别，那很显然这种分支是不好的。“每一支都有较多的类别”就意味着每一支（每个子节点）的熵都很高，纯度很低。这说明这次分裂并没有带来多少有价值的信息，我们仍然无法对子节点中的样本做出有效判断。这样的分裂是低效的、不好的。

---

假设我们有一个数据集，包含14个样本，目标是预测是否“打网球”。其中有9个“是”和5个“否”。

这个根节点的初始熵是：

\[
\text{Entropy}(\text{Root}) = -\left(\frac{9}{14}\log_2\frac{9}{14} + \frac{5}{14}\log_2\frac{5}{14}\right) \approx 0.940
\]

这是一个比较高的熵，代表节点很不纯。

分裂方案A：一个好的分裂（按“天气”特征

假设我们按“天气”这个特征来分裂，得到三个子节点： * 子节点1 (天气=晴天)：包含5个样本 [2个是, 3个否]。 * 这个节点的熵不为0，但纯度比根节点高了一点。 * 子节点2 (天气=阴天)：包含4个样本 [4个是, 0个否]。 * 这个节点的熵为0！它是一个纯节点。所有阴天都去打球了。这是一个非常有价值的信息。 * 子节点3 (天气=雨天)：包含5个样本 [3个是, 2个否]。 * 这个节点的熵也不为0，但纯度也比根节点高了一点。

这个分裂是好的，因为它产生了一个熵为0的纯节点，并且其他节点的纯度也得到了一定提升。

分裂方案B：一个坏的分裂（按“风力”特征）

假设我们按“风力”来分裂，得到两个子节点： * 子节点1 (风力=弱)：包含8个样本 [6个是, 2个否]。 * 熵 \(\approx 0.811\)。 * 子节点2 (风力=强)：包含6个样本 [3个是, 3个否]。 * 熵 \(\approx 1.0\)。这是熵的最大值！

这个分裂是不好的。虽然“风力弱”节点的纯度有所提升，但“风力强”这个节点变得更加不纯了（从9:5变成了3:3）。整体来看，这次分裂提供的信息量有限。

1. C4.5 算法 -> 信息增益率 (Gain Ratio)

   • 核心思想：为了克服 ID3 的缺点，C4.5 引入了信息增益率。它在信息增益的基础上，除以一个“分裂信息”(Split Information)，对取值数目多的特征进行惩罚。

   • 分裂信息：特征本身的不确定性，特征取值越多，分裂信息越大。

     \[
     \text{SplitInfo}(D, A) = -\sum_{v=1}^{V} \frac{|D^v|}{|D|} \log_2\left(\frac{|D^v|}{|D|}\right)
     \]

   • 信息增益率：

     \[
     \text{GainRatio}(D, A) = \frac{\text{Gain}(D, A)}{\text{SplitInfo}(D, A)}
     \]

   • C4.5 就是选择信息增益率最高的特征进行分裂。

2. CART 算法 -> Gini 系数 (Gini Impurity)

   • 适用范围：Classification and Regression Tree (CART)，既能分类也能回归 。现在常见的库（如 scikit-learn）中的决策树多是基于 CART 实现的。
   • 核心思想：选择一个特征进行分裂，使得分裂后的基尼不纯度下降得最多。

   • 基尼不纯度 (Gini Impurity)：表示从一个数据集中随机抽取两个样本，其类别标签不一致的概率。基尼不纯度越小，数据集纯度越高。

     \[
     \text{Gini}(D) = 1 - \sum_{k=1}^{|\mathcal{Y}|} p_k^2
     \]

   • 选择标准：遍历所有特征和所有可能的切分点，计算分裂后的基尼不纯度。选择那个能使基尼不纯度下降最多的分裂方式。

     \[
     \Delta \text{Gini}(A) = \text{Gini}(D) - \sum_{v=1}^{V} \frac{|D^v|}{|D|} \text{Gini}(D^v)
     \]

   • 注意，系数 \(\frac{|D^v|}{|D|}\) 帮助给样本数量较多的分支赋予更高的权重。

   • 优点：与熵的计算相比，基尼系数的计算不涉及对数，计算速度更快。
   • 谨记：每次在一个节点进行分支的时候，都需要在所有可选的特征下，选择一个最好的特征。
   • 最后，在分类问题中，怎么确定每个叶子结点输出的类别呢？看这个叶子结点下哪个类别的样本数多就行了。

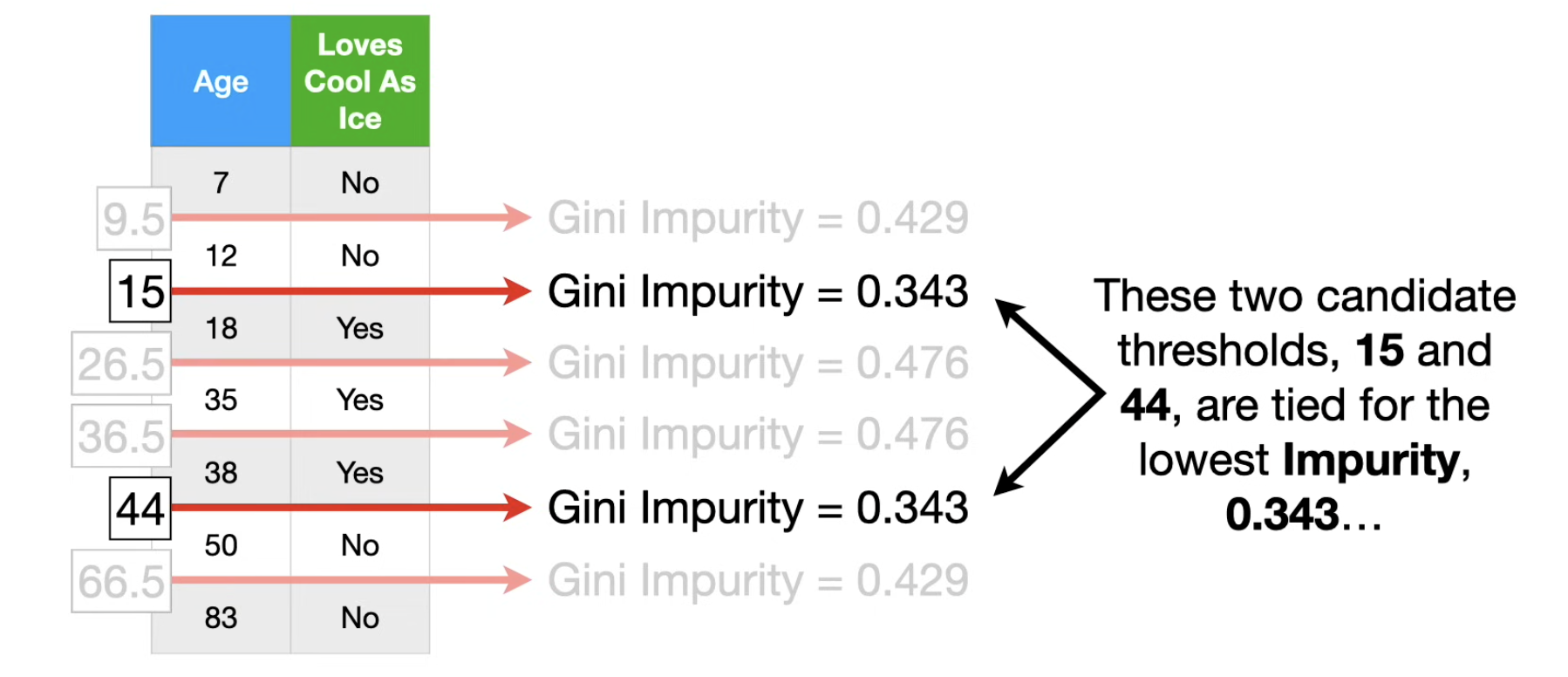
如果是对数值特征（而不是类别特征）进行分类，比如，工作时间 这个特征，此时如何决定分支的阈值参数呢？ （ > ? 是一类，<= 是另一类）

先对所有样本的该特征进行排序，对所有唯一元素，两两取均值，就得到了==该特征下可供分支的所有备选的阈值参数==。

对每个备选的阈值参数，分别计算以这个阈值参数分支后的Gini系数，选出最小的那个，就是==在当前节点处，以该特征进行分支的最好阈值参数了==。

---

针对过拟合的处理 （🌟）

决策树如果不做处理，单个决策树很容易过拟合（学到过多训练数据中的噪声），剪枝是防止过拟合的主要手段。一些策略包括：

• 预剪枝 (Pre-pruning)：在树的生长过程中，提前停止。例如限制树的深度、限制叶子节点的最小样本数等，即使叶子结点不是 Pure 的（不同类都有），但是样本数已经很少了（或者已经Branch了很多层），此时就不需要继续 Branch 了。这个结点就当作叶子结点，输出的值（类别）就是这个结点中数量最多的那个类。
• 后剪枝 (Post-pruning)：先生成一棵完整的决策树，然后自底向上地考察非叶子节点，如果：将该节点对应的子树替换为叶子节点能带来性能提升（如在验证集上），则进行替换。这个步骤也可以视为一个特征选择的过程：在某些阶段，选择某些特征进行分支，甚至可能导致效果更差了。

---

算法复杂度分析

• 训练复杂度：假设有 \(n\) 个样本， \(m\) 个特征。在构建树的每一层，都需要遍历所有特征和所有样本来寻找最佳分裂点。如果特征是连续值，通常需要先排序，排序复杂度为 \(O(n \log n)\)。所以每层的复杂度大约是 \(O(m \times n \log n)\)。树的深度最好情况下是 \(O(\log n)\)。因此，总的训练复杂度较高，粗略估计为 \(O(m \times n \log n \times \text{depth})\)。
• 预测复杂度：非常快。只需要从根节点走到一个叶子节点。树的深度通常是 \(O(\log n)\) 级别，所以预测一个样本的复杂度是 \(O(\log n)\)，或者 \(d_{depth}\)，也就是树的深度。

---

从分类到回归

我们同样可以把上面的用于分类的决策树，变成用于回归分析的，此时每个叶子结点，输出的不再是“属于某个类别”，而是某个概率。

同时，这种方式适合特征较多的情况下，给出“在满足某些特征的约束下，某个事件的概率”，这种问题。。

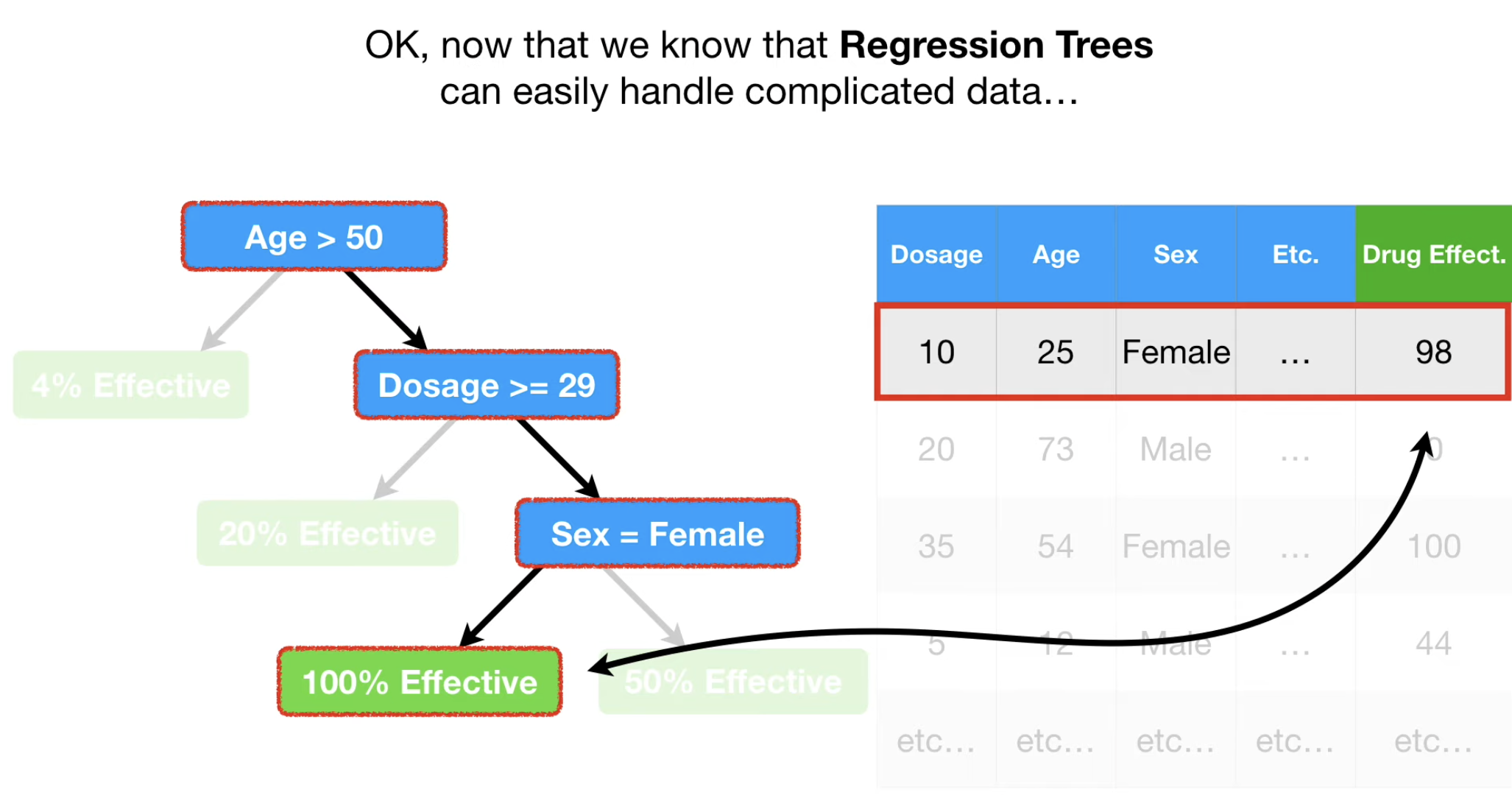
问题就来了，对于一个回归树，在某个特征进行Branch时，如何确定每个结点 branch 的阈值呢？

答案也不难，针对样本中该特征所有数值进行分支，这个分支会把样本分成两部分，每部分给出的预测概率，就是每部分样本真实概率（或者，数值）的均值。然后计算这个均值下，样本的 MSE （均方误差）。找到最小的那个阈值即可。

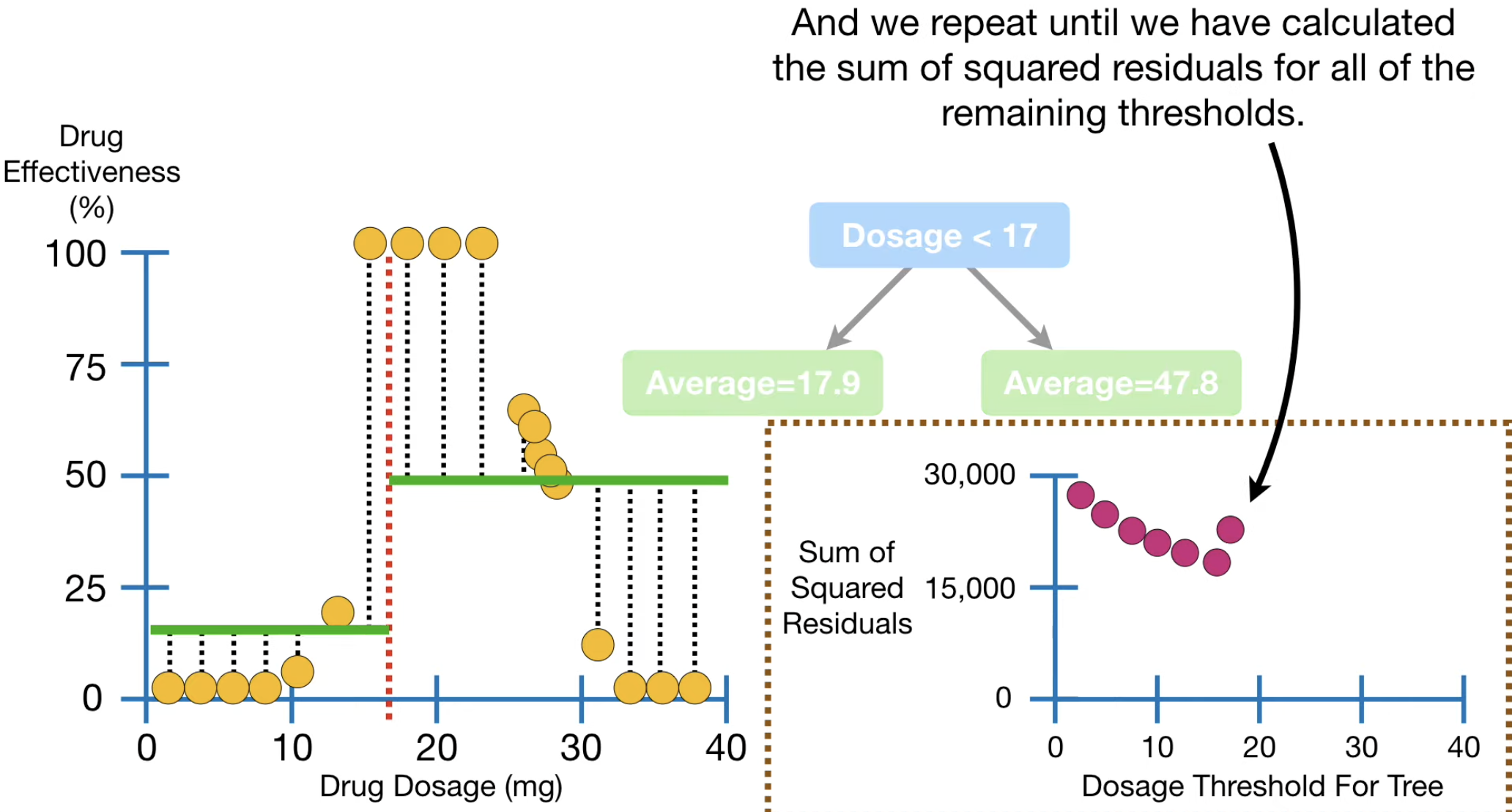
此时，你可以发现，最终建立的这棵树，其输出的叶子结点的“数值”，实际上是“符合某些特征的阈值条件的样本的目标值的均值”。

如法炮制，如果我们有多个特征，那更简单了，我们对每个特征（不管是数值、类别），都可以找到那个最好的分支 threshold，并且可以算出，这个最好的阈值分类下的总平方误差，选择那个最小的，进行分支即可。如下图所示。

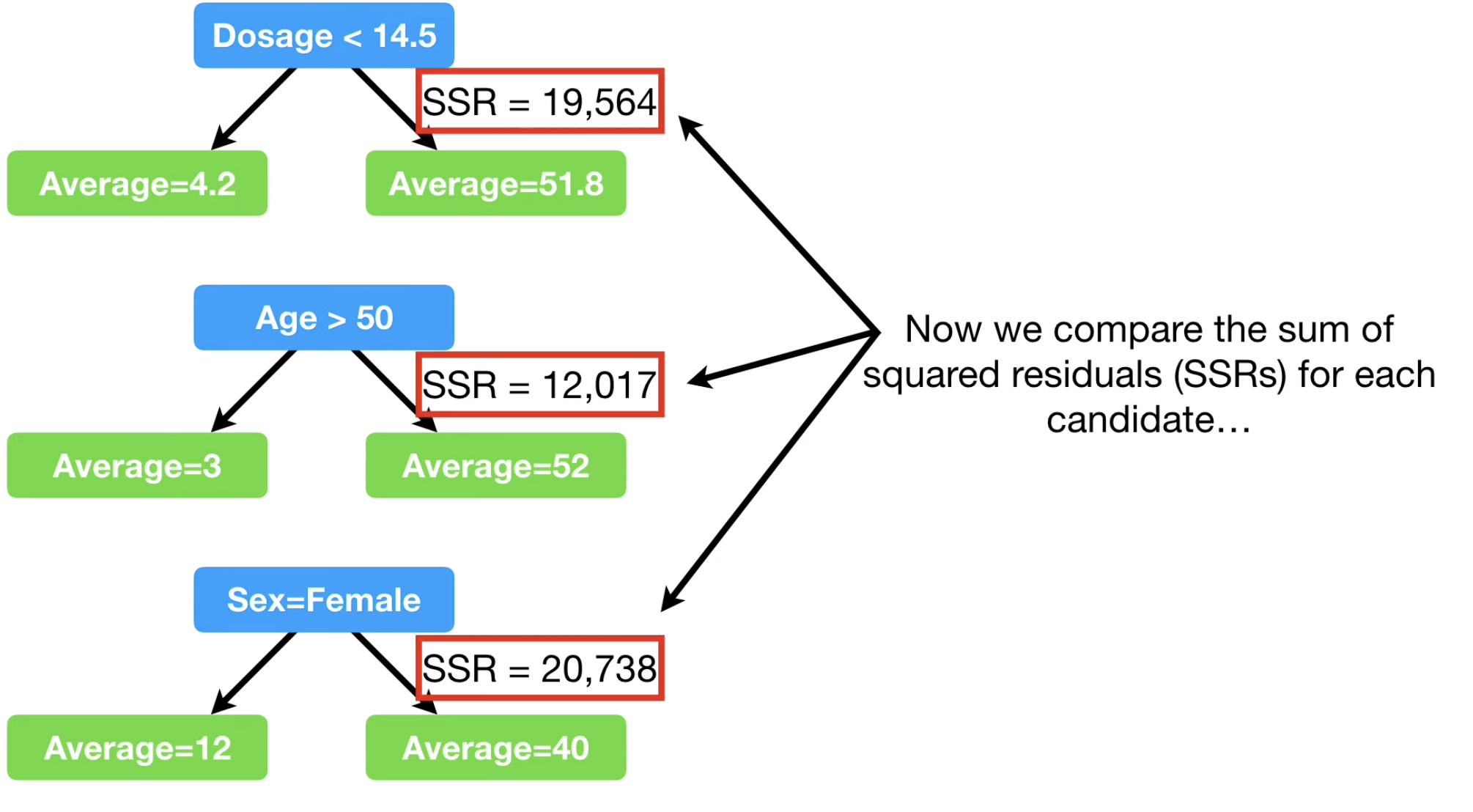
在回归树的情况下，那些常见的防止过拟合的策略依然是 work 的，比如要求某分支的样本数量不得小于某个阈值， 这样，一些node就不会继续分支了。

Cost Complexity Pruning

关于剪枝策略的进一步优化：Cost Complexity Pruning, aka Weakest Link Pruning

代价复杂度剪枝 (Cost-Complexity Pruning, CCP) 是一个非常经典且重要的剪枝策略，它正是 CART (Classification and Regression Trees) 算法中使用的官方后剪枝方法。

CCP 的核心思路是：在“模型准确度”和“模型复杂度”之间进行显式的、可量化的权衡（trade-off）。

它不是简单地看剪掉一个节点后验证集精度是否提升，而是引入一个正则化思想。它定义了一个新的代价函数，既包含树的预测误差，也包含树的复杂度（大小），然后去寻找能最小化这个新代价函数的子树。

这个代价函数，即代价复杂度 (Cost-Complexity)，其定义如下：

\[
R_{\alpha}(T) = R(T) + \alpha|T|
\]

• \(T\)：代表一棵子树。
• \(R(T)\)：树的误差。对于回归树，这通常是这棵树在训练集上的总平方误差和 (SSE)。对于分类树，可以是错分类样本数或者基尼不纯度总和。
• \(|T|\)：树的复杂度，通常用叶子节点的数量来衡量。叶子越多，树越复杂，而==因为过多地进行 Branch 可能导致过拟合==，这个正则项可以认为是用来预防过拟合的。
• \(\alpha\)：复杂度惩罚参数 (Complexity Parameter)，这是一个非负的超参数（\(\alpha \ge 0\)）。它控制着我们对模型复杂度的惩罚力度。

核心思路可以总结为：对于一个给定的 \(\alpha\)，CCP 会找到一棵子树 \(T\)，使得 \(R_{\alpha}(T)\) 的值最小。 1. 如果 \(\alpha = 0\)，没有复杂度惩罚，那么最优的树就是未剪枝的、最完整的树 \(T_0\)，因为它的训练误差 \(R(T_0)\) 最小。 2. 如果 \(\alpha \to \infty\)，我们对复杂度的惩罚极重，任何一个多余的叶子节点都会带来巨大的代价。此时，最优的树就是一个只包含根节点的树（\(|T|=1\)），因为它最简单。

比如，对于 后剪枝 策略来说（将一些叶子结点删掉，不在某些结点继续 Prune，那么如何选择删去哪些叶子结点呢？）

我们可以保留下每个叶子结点导致的 MSE （下图中为 Sum of Squred Residuals，类似），这样计算出整棵树导致的 MSE。

---

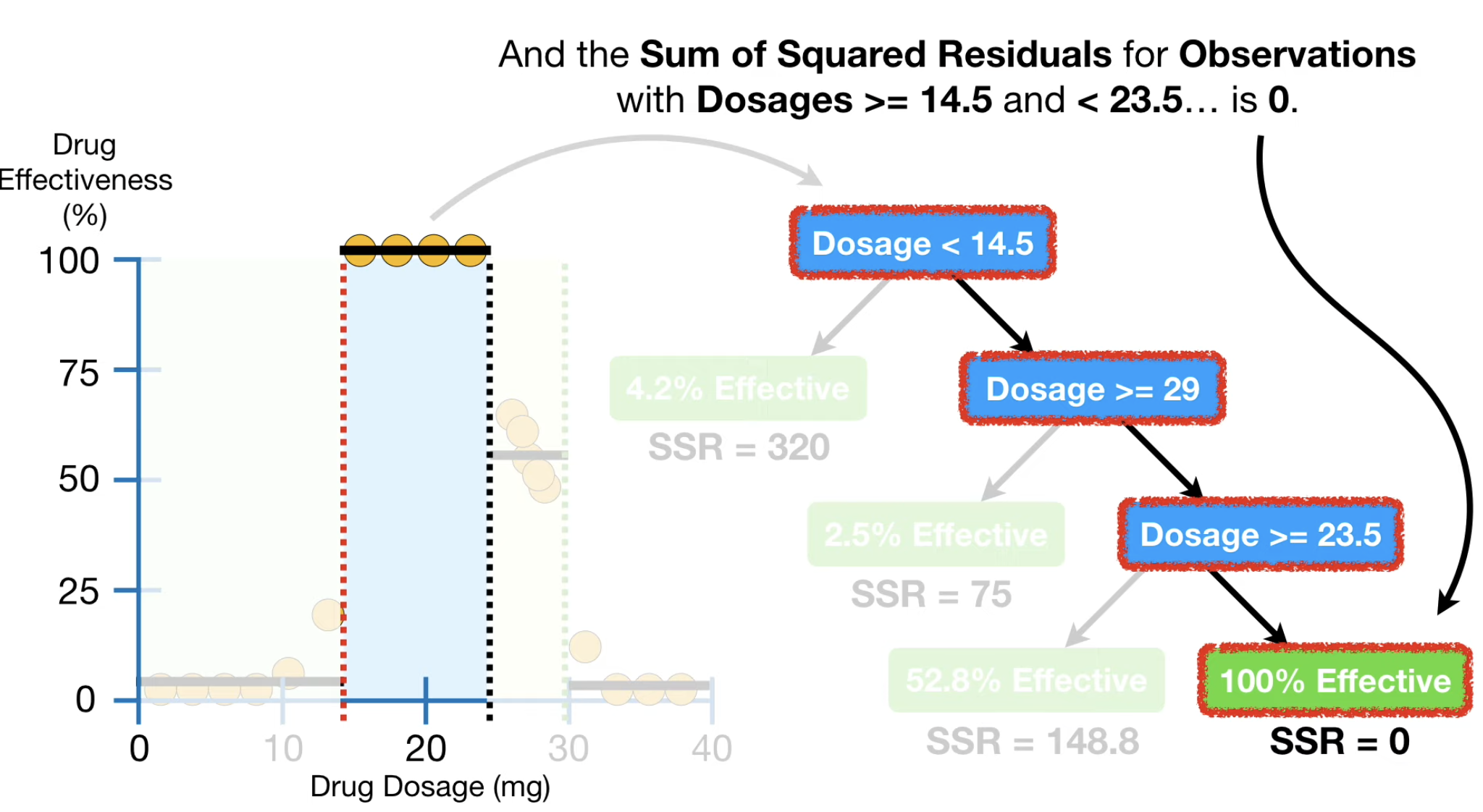
我们来一步步拆解它。

有效防止过拟合：这是所有剪枝策略的共同目标。通过简化模型，CCP 降低了模型对训练数据噪声的拟合程度，从而提升了在未见数据上的泛化能力。

提供一个最优的子树序列：CCP 最独特的优点是，它不只是给出一个剪枝后的树，而是能够生成一个从完整大树到根节点树的、嵌套的、最优子树序列。这为后续选择最佳模型提供了极大的便利。

这个别名的由来非常形象地解释了算法的内在逻辑。

1. 从完整树 \(T_0\) 开始：我们有一棵生长到最大的树。
2. 寻找“最弱的一环”：在树 \(T_0\) 中，我们考察每一个非叶子节点。如果我们将某个内部节点 \(t\) 下方的整个子树剪掉，使其自身成为一个叶子节点，会发生什么？
   • 误差会增加：因为这个新叶子节点的预测值（均值）肯定不如原来那片精细的子树预测得准。我们记误差增加量为 \(\Delta R\)。
   • 复杂度会减小：原来的子树有很多叶子，现在变成了一个。我们记叶子节点减少量为 \(\Delta |T|\)。

3. 计算“性价比”：我们可以为每个潜在的剪枝点（即每个内部节点）计算一个“性价比”指标 \(g(t)\)：

   \[
   g(t) = \frac{R(t) - R(T_t)}{|T_t| - 1} = \frac{\Delta R}{\Delta |T|}
   \]

   • \(R(t)\) 是将节点 \(t\) 剪成叶子后的误差。
   • \(R(T_t)\) 是未剪枝前，节点 \(t\) 下方整个子树 \(T_t\) 的总误差。
   • \(|T_t|\) 是子树 \(T_t\) 的叶子数。
   • 这个 \(g(t)\) 的含义是：剪掉这个子树，我们每减少一个叶子节点，会换来多大的误差增幅。

4. 剪掉最弱的：\(g(t)\) 值最小的那个节点，就是“最弱的一环”。因为剪掉它“最划算”——用最小的误差代价，换来了复杂度的降低。

5. 迭代过程：算法会找到 \(g(t)\) 最小的那个节点，并将其剪枝，得到一棵更小的树 \(T_1\)。然后，在这个 \(T_1\) 上重复上述过程，找到下一个“最弱环节”并剪掉，得到 \(T_2\)……如此往复，直到最后只剩下根节点。

这个过程就产生了一个子树序列 \([T_0, T_1, T_2, ..., T_{root}]\)。可以证明，这个序列中的每一棵树 \(T_k\)，都是在某个特定的 \(\alpha_k\) 值下的最优子树。

3. 与其他剪枝策略的区别

对比维度	代价复杂度剪枝 (CCP)	预剪枝 (Pre-pruning)	简单后剪枝 (Simple Post-pruning)
执行时机	后剪枝：在树完全生成后进行。	预剪枝：在树的生长过程中进行。	后剪枝：在树完全生成后进行。
决策依据	全局的代价复杂度函数 \(R_{\alpha}(T)\)。通过一个超参数 \(\alpha\) 平衡误差与复杂度。	固定的、启发式的阈值，如 max_depth, min_samples_leaf, min_impurity_decrease。	独立的验证集。比较剪枝前后的验证集精度。
过程与结果	系统性地生成一个最优子树序列，然后通过交叉验证选择最佳的 \(\alpha\) 对应的树。	一次性生成一棵最终的树。过程简单直接。	自底向上，贪心地逐个节点判断是否剪枝。最终也只生成一棵树。
优点	1. 更鲁棒，不易错过好的子树。 2. 通过交叉验证选择 \(\alpha\)，模型选择更可靠。 3. 结果是一个优化问题的解，更具理论依据。	1. 速度快，因为树从未完全生长。 2. 算法简单，易于实现。	比预剪枝视野更广，因为看到了完整的树。
缺点	计算量比预剪枝大。	1. 贪心本质，可能过早停止生长，导致欠拟合。 2. 阈值是超参数，选择困难。	也可能因贪心而陷入局部最优，剪掉不该剪的节点。

总结一下：

• 分类树的目标：最大化纯度。它使用的分裂标准是基尼不纯度 (Gini Impurity) 或 信息增益 (Information Gain)，目标是让分裂后的子节点中类别尽可能单一。

• 回归树的目标：最小化预测误差。它没有“纯度”的概念，因为目标值是连续的。它衡量一次分裂好坏的标准是：分裂后的两个子区域内，样本的方差或均方误差 (Mean Squared Error, MSE) 是否足够小。

复盘流程

假设我们要在某个节点上进行分裂，算法会执行以下操作：

1. 遍历每一个特征 \(j\)。
2. 对于选定的特征 \(j\)，遍历该特征所有可能的取值 \(s\) 作为切分点（对于连续特征，通常是两个相邻取值的中点）。
3. 每一次尝试（即选择一个特征 \(j\) 和一个切分点 \(s\)）都会将当前节点的数据集 \(D\) 分成两个子集：
   • \(D_1 = \{(x, y) | x_j \le s\}\)
   • \(D_2 = \{(x, y) | x_j > s\}\)

4. 计算分裂后的误差。最常用的误差度量是平方误差和 (Sum of Squared Errors, SSE)。

   • 首先，计算出两个子集的预测值（即各自样本的均值）：\(c_1 = \text{mean}(y_i | x_i \in D_1)\) 和 \(c_2 = \text{mean}(y_i | x_i \in D_2)\)。

   • 然后，计算这两个子集内的总平方误差和：

     \[
     \text{SSE}(j, s) = \sum_{x_i \in D_1} (y_i - c_1)^2 + \sum_{x_i \in D_2} (y_i - c_2)^2
     \]

5. 选择最优分裂：算法会选择那个能使分裂后总 SSE 最小化的特征 \(j^*\) 和切分点 \(s^*\)。

   \[
   (j^*, s^*) = \arg\min_{j,s} \left[ \text{SSE}(j, s) \right]
   \]

这个过程会递归地在每个新生成的子节点上进行，直到满足停止条件（如达到最大深度、节点样本数过少等）。

复盘一下复杂度

• 构建整棵树：

  • 这个寻找最佳分裂点的过程会在树的每一层、每个节点上重复进行。
  • 总的训练复杂度与分类树处于同一数量级，粗略估计为 \(O(\text{depth} \times m \times n \log n)\)，其中 \(n\) 是总样本数。

• 预测复杂度：

  • 与分类树完全相同。对于一个新样本，只需要从根节点开始，沿着树的分支向下走，直到到达一个叶子节点。其复杂度只与树的深度有关，即 \(O(\text{depth})\)。对于一棵平衡树，深度约为 \(O(\log n)\)。

这是一个简单的对比表格：

对比维度	分类树 (Classification Tree)	回归树 (Regression Tree)
解决问题	预测离散的类别标签	预测连续的数值
核心分裂标准	信息增益 或 基尼不纯度 (目标：使节点纯度最高)	平方误差和 (SSE) 或 均方误差 (MSE) (目标：使节点内方差最小)
叶节点输出	落在该叶节点样本的众数 (Mode)	落在该叶节点样本的均值 (Mean)
模型评估	准确率、精确率、召回率、F1 等	均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)等
算法复杂度	基本相同	基本相同

---