Boosting ｜ GBDT⚓︎

约 5821 个字 2 张图片预计阅读时间 19 分钟总阅读量次

GBDT (Gradient Boosting Decision Tree)，即梯度提升决策树，是当今工业界和数据科学竞赛中使用最广泛、效果最好的机器学习算法之一。它也是理解 XGBoost、LightGBM 和 CatBoost 等更先进算法的基础。

与 AdaBoost 通过提升错分样本的权重来学习不同，GBDT 的核心思想是，每一棵新的树都是为了拟合和修正上一棵树留下的残差（Residual）。更一般地说，是拟合损失函数的负梯度 。

本文首先讨论用作回归任务的场景。区别于Adaboost在于，不用小的 Stump 了，而是用一些尺寸相同但是限制规模的树（比如，8个叶子，或者32个叶子节点）按顺序组成。

更重要的是，我们不再单单对预测值进行学习，而是对“某个预测值的残差进行学习”。

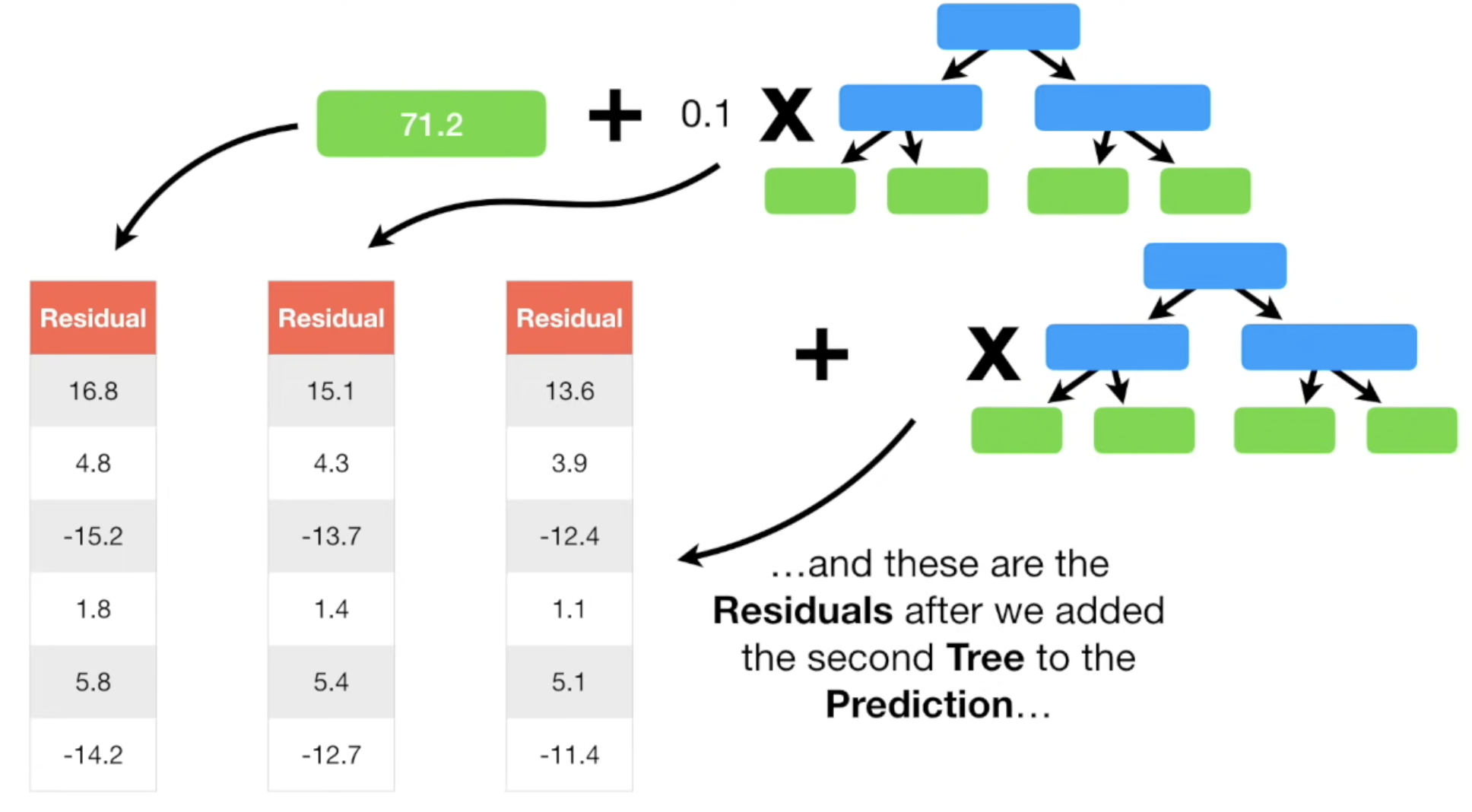
每一个新建立的小树，都会学习先前的残差（加上一个特定的学习率），类似一次走一小步，每次逼近一点“正确的方向”。每次都在前一个“预测值”的基础上，学习残差。

终止条件是：Residual 的减少不明显了，或者到达一定迭代次数了。

1. 使用场景⚓︎

GBDT 是一个非常通用的框架，既能用于回归问题，也能用于分类问题，并且在两者上都表现出色。

回归问题：这是 GBDT 最直观的应用。例如预测房价、预测股票价格、预测用户停留时长等。
分类问题：通过使用不同的损失函数（如对数损失函数），GBDT 在分类任务上同样强大。例如广告点击率（CTR）预测、信用风险评估、用户流失预测等。
排序问题：GBDT 也可以用于学习排序（Learning to Rank），如搜索结果排序。

由于其高精度、可解释性（可以输出特征重要性）以及对多类型数据的良好处理能力，GBDT 在各大公司的推荐、风控、搜索等核心业务中扮演着至关重要的角色。

2. 核心思想：拟合残差与梯度下降⚓︎

GBDT 的思想比 AdaBoost 更进了一步，也更为通用。我们可以从两个层面来理解它。

直观理解（以回归为例）：假设我们正在做一个预测年龄的任务，第一个基学习器（一棵树）预测某人的年龄是30岁，但他的真实年龄是35岁。那么模型就留下了 5 岁的残差（residual = 35 - 30 = 5）。GBDT 的下一步就是训练第二棵树，这棵树不再以人的特征为输入、年龄为输出来学习，而是以人的特征为输入、5岁这个残差为输出来学习。如果第二棵树成功预测了这个残差，那么 新预测 = 30 + 5 = 35，就命中了真实值。当然，第二棵树也不可能完美预测，它会留下新的、更小的残差。GBDT 就是这样一轮一轮地通过训练新树来不断减少之前模型留下的总残差，从而逼近真实值。
数学理解（梯度下降）： GBDT 的精髓。GBDT 将模型的优化过程看作是在函数空间（Function Space）中的梯度下降。
- 我们的目标是找到一个模型 $F(x)$，使得所有样本的损失函数 $L(y, F(x))$ 之和最小。
- GBDT 是一个加法模型，最终模型 $F_M(x)$ 是由 $M$ 棵树累加而成的：$F_M(x) = F_0(x) + F_1(x) + ...$。
- 在第 $m$ 步，我们已经有了模型 $F_{m-1}(x)$，我们希望找到一棵新树 $h_m(x)$，使得损失函数进一步下降：$L(y, F_{m-1}(x) + h_m(x))$。
- GBDT 使用了梯度下降的思路来近似求解。它计算出当前损失函数相对于模型预测值 $F_{m-1}(x)$ 的负梯度，并将这个负梯度值作为本轮要拟合的目标（即“残差”）。
```
\[
\text{本轮拟合目标} \approx - \left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]_{F(x) = F_{m-1}(x)}
\]
```
这个负梯度被称为伪残差（Pseudo-residual）。 * 当损失函数是均方误差 $L = \frac{1}{2}(y - F(x))^2$ 时，其负梯度恰好就是 $y - F(x)$，也就是我们直观理解中的“残差”。 * 当损失函数是其他函数（如用于分类的对数损失）时，负梯度就不再是简单的“真实值-预测值”，但其作为“修正方向”的意义是不变的。

因此，GBDT 的每一轮迭代，都是在训练一棵树来拟合当前所有样本损失函数的负梯度。

3. 算法流程 (回归任务 + CART 树为例)⚓︎

假设训练集为 $T = \{(x_1, y_1), ..., (x_N, y_N)\}$，损失函数为均方误差 $L(y, F(x)) = \frac{1}{2}(y - F(x))^2$，迭代次数为 $M$，弱学习器为 CART 回归树。

初始化模型 用一个常数值来初始化模型，使得损失函数最小。对于均方误差，这个值就是所有样本 $y$ 值的平均数。
```
\[
F_0(x) = \bar{y} = \frac{1}{N}\sum_{i=1}^{N} y_i
\]
```
进行 M 轮迭代 对 $m = 1, 2, ..., M$：

a. 计算伪残差（负梯度）：对每一个样本 $i=1, ..., N$，计算它在当前模型 $F_{m-1}(x)$ 下的伪残差。
```
\[
r_{im} = - \left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]_{F(x) = F_{m-1}(x)} = y_i - F_{m-1}(x_i)
\]
```
b. 训练一棵回归树：将伪残差 $r_{im}$ 作为新的目标值，将原始特征 $x_i$ 作为输入，得到一个新的训练集 $\{(x_i, r_{im})\}_{i=1}^N$。使用这个新数据集训练一棵 CART 回归树 $h_m(x)$。这棵树会将输入空间划分为 $J_m$ 个不相交的区域（叶子节点）$R_{1m}, R_{2m}, ..., R_{J_m m}$。

c. 更新模型的叶子节点输出：对于每个叶子节点区域 $R_{jm}$，计算出该区域内使损失函数最小的最佳拟合值 $\gamma_{jm}$ (也称作叶子节点的权重)。对于均方误差，这个值就是该区域内所有样本残差的平均值。
```
\[
\gamma_{jm} = \arg\min_{\gamma} \sum_{x_i \in R_{jm}} L(y_i, F_{m-1}(x_i) + \gamma) \approx \text{mean}_{x_i \in R_{jm}}(r_{im})
\]
```
d. 更新总模型：将新生成的树加入到总模型中，通常会乘以一个学习率（Learning Rate） $\eta$ ，用于防止过拟合。
```
\[
F_m(x) = F_{m-1}(x) + \eta \cdot h_m(x)
\]
```
其中 $h_m(x)$ 的输出是对应叶子节点的 $\gamma_{jm}$ 值。
最终模型 经过 $M$ 轮迭代，最终的强学习器就是所有树的加权（通过学习率）累加。
```
\[
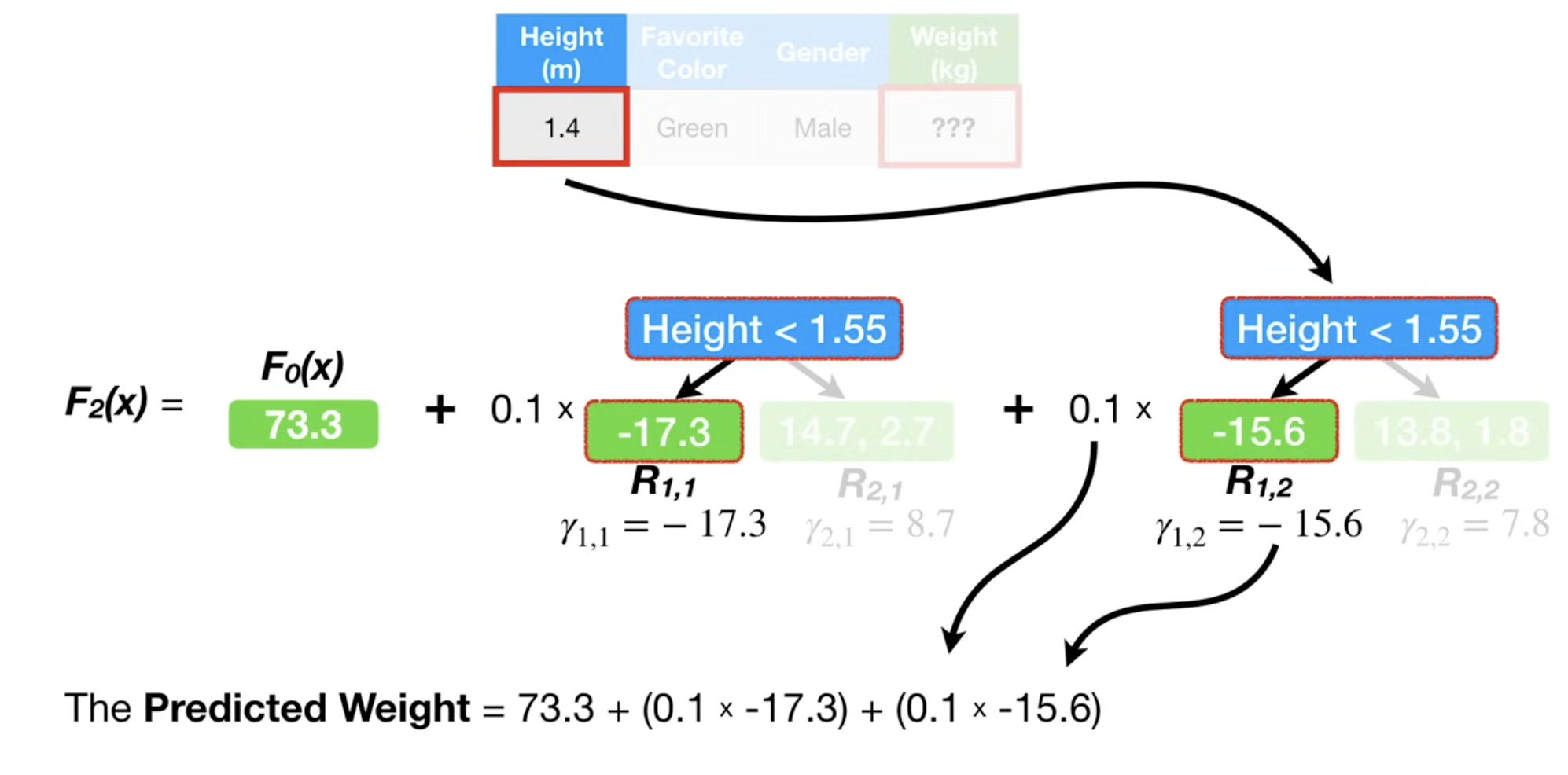
F_M(x) = F_0(x) + \eta \sum_{m=1}^{M} h_m(x)
\]
```

4. 算法复杂度⚓︎

训练复杂度：训练过程是 GBDT 最耗时的部分。其复杂度主要取决于迭代次数 $M$ 和每轮迭代中决策树的构建成本。
- 在每一轮迭代中，首先要计算所有 $N$ 个样本的伪残差，复杂度为 $O(N)$。
- 接下来是训练一棵决策树，这是最耗时的步骤。对于一棵深度为 $D_{tree}$ 的树，使用 $N$ 个样本和 $d$ 个特征，构建成本近似为 $O(N \cdot d \cdot D_{tree})$ 或 $O(N \cdot d \cdot \text{num\_leaves})$。更精确地，如果对每个特征的取值进行排序来寻找分裂点，复杂度会接近 $O(N \log N \cdot d)$。
- 总的训练复杂度为：
```
\[
\text{复杂度}_{\text{train}} \approx O(M \cdot (N \cdot d \cdot D_{tree}))
\]
```
由于是串行过程，GBDT 的训练通常比较慢。
推理复杂度：与 AdaBoost 类似，GBDT 的推理过程很快。对于一个新样本 $x$：
- 需要将它输入到 $M$ 棵树中，分别得到预测值（叶子节点值）。
- 每棵树的预测过程是沿树的路径从根走到叶，复杂度为 $O(D_{tree})$。
- 将所有树的结果与学习率相乘并累加。
- 总的推理复杂度为：
```
\[
\text{复杂度}_{\text{inference}} = O(M \cdot D_{tree})
\]
```
这个复杂度与训练样本数 $N$ 和特征维度 $d$ 无关，因此推理速度很快。

4.5 核心流程/伪代码/推导⚓︎

Input: Data ${(x_i, y_i)}^n_{i = 1}$， Loss Function $L(y_i, F(x))$

对于回归问题，损失函数选择的是 Sum of squared error

Step 1: Initialize model with const value $F_0(x) = \arg \min_{\gamma} \sum^n_{i = 1}L(y_i, \gamma)$

初始值，是那个能够最小化损失函数的值，在当前 Sum of squared error 的情况下，就等于均值。

Step 2: for $m=1$ to $M$:

(A) Compute $r_{im} = -\left[\frac{\partial L(y_{i},F(x_{i}))}{\partial F(x_{i})}\right]{F(x)=F $for }(x)$i=1,\ldots,n$

根据当前预测值，计算每一个样本的负梯度方向，用来表示预测残差，由于我们用的 Sum of squared error，也就是： - (observed - pred) * (-1) = (observed - pred)

这个式和逻辑回归惊人地相似！

(B) Fit a regression tree to the $r_{im}$values and create terminal regions $R_{jm}$, for $j=1\ldots J_{m}$

这一步的作用，是构建残差树，并且给样本数据进行划分。每个样本数据被划分到一个叶子节点中。

(C) For $j = 1 \ldots J_{m}$ compute $\gamma_{jm} = \underset{\gamma}{\operatorname{argmin}} \sum_{x_{i} \in R_{ij}} L(y_{i},F_{m-1}(x_{i})+\gamma)$

计算出残差树中，每个叶子结点的输出值（作为一种残差的修正！）

这个输出值 $\gamma$ 的含义是，添加了这个修正之后，能够最明显地修正（用原先预测值+这个决策树处理后）的残差。体现在数学公式上，就是最小化“原先预测值 + 修正值 $\gamma$ 后”的损失函数。

这个输出的 $\gamma$ 还可以理解为，对于现在这个决策树叶子结点（其实就是前面一步写的 $R_{jm}$ 区域内的所有样本，我需要调整多少，才能使得加上这些误差后，样本的预测误差尽可能地小？

也就是 $\arg \min \dfrac{1}{2} (y_i - (F_{m - 1}(x_i) + \gamma))^2$

用链式法则推导即可发现，$\gamma$ 取残差的均值即可。

$\text{mean}_{x_i \in R_{jm}}(r_{im})$

(D) Update $F_{m}(x) = F_{m-1}(x) + \nu \sum_{j=1}^{J_{m}} \gamma_{m} I(x \in R_{jm})$

这里推理的时候，可以发现，其实它的迭代还是基于不断地学习前一次回归预测时的残差，不断修正来进行的。

5. 优缺点总结⚓︎

优点: * 预测精度高：GBDT 在各类数据集上通常都能取得非常高的精度。 * 适用范围广：能处理回归、二分类、多分类等多种任务。 * 对异常值有一定鲁棒性：相较于 AdaBoost，如果使用一些对异常值不敏感的损失函数（如 Huber loss），GBDT 的鲁棒性更强。 * 可解释性强：可以输出特征重要性，便于理解模型决策。

缺点: * 训练过程串行，难以并行：同 AdaBoost 一样，后一棵树的训练依赖于前一棵树的结果，难以并行化，导致训练速度较慢。 * 参数众多，调参复杂：GBDT 的超参数较多（如学习率 learning_rate、树的数量 n_estimators、树的深度 max_depth、子采样比例 subsample 等），调参需要一定的经验。 * 容易过拟合：如果参数设置不当（如树的数量太多、深度太深），GBDT 也很容易过拟合。

用于分类的 GBDT⚓︎

思路是一样的，首先从一个General的预测值入手，后续的每一棵树都用来拟合前一棵树的残差。

当 GBDT 用于分类时，我们不再是去直接预测一个类别标签（如 0 或 1），而是去预测样本属于某个类别的概率。更准确地说，是预测这个概率对应的对数几率（log-odds）。

也就是，我们初始的预测值，是 $\log(odd)$，odd = 样本为正的数量 / (总量 - 样本为正的数量)。

log odds 公式

然后，用sigmoid公式，将这个 log odds 转化成0-1之间的概率分布：

\[\dfrac{1}{1 + e^{- \log (odds)}}\]

现在，我们相当于知道了一个概率，我们的残差如何计算？只需要用样本的情况（0，1），减去概率即可。

好的，我们接着深入 GBDT。在面试中，能够清晰地阐述 GBDT 如何从回归任务推广到分类任务，是展现你对算法理解深度的绝佳机会。

与回归任务相比，用 GBDT 做分类的核心区别在于损失函数 (Loss Function) 和模型输出的意义。下面我们来详细拆解。

GBDT 用于分类与回归的核心区别⚓︎

损失函数不同:
- 回归: 通常使用均方误差 (Mean Squared Error, MSE)。
- 分类: 通常使用对数损失函数 (Log-Loss)，也称为二项偏差 (Binomial Deviance)。
模型输出的意义不同:
- 回归: GBDT 的总输出 $F_M(x)$ 直接就是最终的预测值。
- 分类: GBDT 的总输出 $F_M(x)$ 是一个原始的、未归一化的分数（我们称之为对数几率, log-odds）。这个分数需要通过一个连接函数 (Link Function)（对于二分类，是 Sigmoid 函数）转换成一个 0 到 1 之间的概率值。

算法流程 (以二分类为例)⚓︎

假设我们的标签 $y \in \{0, 1\}$。

1. 损失函数与连接函数

对数损失函数 (Log-Loss):
```
\[
L(y, p) = -(y \log(p) + (1-y)\log(1-p))
\]
```
这里的 $p$ 是模型预测样本为类别 1 的概率。
Sigmoid 函数: 我们用 Sigmoid 函数将模型的原始输出 $F(x)$ 映射到概率 $p$。
```
\[
p(x) = \text{sigmoid}(F(x)) = \frac{1}{1 + e^{-F(x)}}
\]
```

2. 算法详细流程

初始化模型 与回归任务中用均值初始化不同，这里我们需要找到一个常数值 $F_0(x)$ 来最小化总的对数损失。这个最优的初始值是所有样本标签的对数几率 (log-odds)。
```
\[
F_0(x) = \ln\left(\frac{\sum y_i}{N - \sum y_i}\right) = \ln\left(\frac{\text{mean}(y)}{1 - \text{mean}(y)}\right)
\]
```
在 $F_0(x)$ 下，模型对所有样本的初始预测概率都是 $p_0 = \text{mean}(y)$。
进行 M 轮迭代 对 $m = 1, 2, ..., M$：

a. 计算伪残差（负梯度）：这是最关键的一步。我们需要计算损失函数 $L$ 对上一轮模型输出 $F_{m-1}(x)$ 的负梯度。对于第 $i$ 个样本，首先计算它在当前模型下的预测概率：
```
\[
p_{i, m-1} = \text{sigmoid}(F_{m-1}(x_i))
\]
```
然后计算伪残差。对于对数损失函数，其负梯度有一个非常简洁和直观的形式：
```
\[
r_{im} = - \left[ \frac{\partial L(y_i, p)}{\partial p} \frac{\partial p}{\partial F(x_i)} \right]_{F(x) = F_{m-1}(x)} = y_i - p_{i, m-1}
\]
```
没错，伪残差就是真实标签（0或1）与上一轮预测概率之间的差值！ 这非常直观：如果模型预测概率偏低（$p$ 小于 $y$），残差为正，下一棵树就要学习一个正值来拉高预测；反之亦然。

b. 训练一棵回归树：和回归 GBDT 完全一样，我们使用新的数据集 $\{(x_i, r_{im})\}_{i=1}^N$ 来训练一棵 CART 回归树 $h_m(x)$，拟合这些伪残差。

c. 更新模型的叶子节点输出：这一步比回归 GBDT 稍复杂。我们不能简单地将叶子节点内残差的均值作为输出。需要找到一个最优的叶子节点输出值 $\gamma_{jm}$，使得加上这个值后，总损失最小。在标准的 GBDT 实现中，这个最优值的计算公式为：
```
\[
\gamma_{jm} = \frac{\sum_{x_i \in R_{jm}} r_{im}}{\sum_{x_i \in R_{jm}} [p_{i, m-1}(1 - p_{i, m-1})]}
\]
```
理解起来就是，这个叶子节点下所有样本，在前一次迭代时候的预测概率乘以（1-预测概率）的和。

分母是每个样本在上一轮预测概率下对应的Hessian矩阵（二阶导数）的相反数。这实际上是应用了一步牛顿-拉夫逊法来寻找最优解。XGBoost 正是把这个思想发扬光大。对于面试，你能说出“不仅仅是均值，而是要考虑二阶信息”就已经很加分了。

d. 更新总模型：与回归 GBDT 一样，使用学习率 $\eta$ 进行缩放更新。
```
\[
F_m(x) = F_{m-1}(x) + \eta \cdot h_m(x)
\]
```
最终预测 经过 $M$ 轮迭代，得到最终模型 $F_M(x)$。
- 要获得概率：将最终的原始分数输入 Sigmoid 函数。
```
\[
\hat{p}(x) = \text{sigmoid}(F_M(x))
\]
```
- 要获得类别：将得到的概率与阈值（通常是0.5）比较。
```
\[
\hat{y}(x) = \begin{cases} 1 & \text{if } \hat{p}(x) > 0.5 \\ 0 & \text{otherwise} \end{cases}
\]
```
  这等价于直接判断 $F_M(x)$ 的正负。

算法复杂度⚓︎

训练复杂度：与回归 GBDT 完全相同。在每一轮迭代中，主要的计算开销依然是构建决策树。计算伪残差和更新叶子节点值的复杂度都是 $O(N)$，而构建树的复杂度远大于此。因此，总训练复杂度依然是：
```
\[
\text{复杂度}_{\text{train}} \approx O(M \cdot (N \cdot d \cdot D_{tree}))
\]
```
推理复杂度：与回归 GBDT 完全相同。推理时，同样需要将样本输入 $M$ 棵树并累加结果。最后多了一步 Sigmoid 函数的计算，但其开销可以忽略不计。总推理复杂度依然是：
```
\[
\text{复杂度}_{\text{inference}} = O(M \cdot D_{tree})
\]
```

核心流程的伪代码、推导⚓︎

这里非常建议对比着前面“分类”部分的伪代码和推导来分析，可以直观感受到损失函数不同给梯度推导、叶子结点输出的残差计算方式带来的影响，以及预测概率 $p$ 与输入值 $\log(\text{odds})$ 的巧妙变换的。

Input: Data ${(x_i, y_i)}^n_{i = 1}$， Loss Function $L(y_i, F(x))$

对于分类问题，损失函数选择的是 对数损失函数（多分类下的交叉熵）

我们可把 $y_i \log p + (1-y_i) \log (1 - p)$ 的损失函数，改写成与 Log Odds 有关的公式！

这里 Follow 一个重点，即，我们给出的预测概率 p，和我们输入函数的 log(odds) 之间的转换公式，为：

$p = \text{sigmoid}(\log(\text{odds}))$

而我们有 sigmoid 函数： $\text{sigmoid}(x) = \dfrac{1}{1 + e^{-x}}$

所以，$p = \dfrac{e^{\log(\text{odds})}}{1 + e^{\log(\text{odds})}}$

所以，我们的损失函数可以用 $\log (\text{odds})$ 和 $p$ 两个式子分别来表示。

也就是:

\[\min - ( y\log(\text{odds}) - \log (1 + e^{\log(\text{odds})}) )\]

或者说：

\[\min - ( y \log (\dfrac{p}{1 - p}) + \log (1 - p))\]

我们希望交叉熵尽可能地大，所以希望最小化负的交叉熵。

这里的 y 表示的是样本属于某类的真实概率（1或者0）。

Step 1: Initialize model with const value $F_0(x) = \arg \min_{\gamma} \sum^n_{i = 1}L(y_i, \gamma)$

初始值，是那个现有数据中能够最小化损失函数的值，在当前 Log Loss 损失函数的情况下，就等于原先所有样本的 $\log (\text{odds})$。

Step 2: for $m=1$to $M$:

(A) Compute $r_{im} = -\left[\frac{\partial L(y_{i},F(x_{i}))}{\partial F(x_{i})}\right]_{F(x)=F_{m-1}(x)}$ for $i=1,\ldots,n$

根据当前预测值，计算每一个样本的负梯度方向，用来表示预测残差，由于我们用的 Log Loss，梯度方向： $-($ observed $-$ $\dfrac{e^{\log(\text{odds})}}{1 + e^{\log(\text{odds})}})$，由此可得我们的残差：

\[\text{observed} - \dfrac{e^{\log(\text{odds})}}{1 + e^{\log(\text{odds})}}\]

(B) Fit a regression tree to the $r_{im}$ values and create terminal regions $R_{jm}$, for $j=1\ldots J_{m}$

这一步的作用，是构建残差树，并且给样本数据进行划分。每个样本数据被划分到一个叶子节点中，并且我们也有了残差 $r_{im}$ 的数据。

(C) For $j=1\ldots J_{m}$ compute $\gamma_{jm} = \underset{\gamma}{\operatorname{argmin}} \sum_{x_{i} \in R_{ij}} L(y_{i},F_{m-1}(x_{i})+\gamma)$

计算出残差树中，每个叶子结点的输出值（作为一种残差的修正！）

这个输出值 $\gamma$ 的含义是，添加了这个修正之后，能够最明显地修正（用原先预测值+这个决策树处理后）的残差。这里的 $F_{m - 1}(x_i)$ 实际上就是 $\log (\text{odds})$.

做分类时候的叶子结点的输出比较难以计算，要用到二阶Taylor展开。这里用 $p$ (前一棵树计算出来的它为正样本的概率) 来写更加简洁。

\[
\gamma_{jm} = \frac{\sum_{x_i \in R_{jm}} r_{im}}{\sum_{x_i \in R_{jm}} [p_{i, m-1}(1 - p_{i, m-1})]}
\]

注意，这里的 $p_{i,m - 1}$ 对于每一个样本来说，在后面会是越来越不同的。

(D) Update $F_{m}(x) = F_{m-1}(x) + \nu \sum_{j=1}^{J_{m}} \gamma_{m} I(x \in R_{jm})$

在推理时，你可以发现我们始终输出的是一个 $\log (odds)$，我们的叶子结点对残差的修正，其实就是一种“对 $\log(\text{odds})$ 的修正。

我们整个流程，就是对原先 $\log(\text{odds})$ 的预测结果，每次建立一个稍微弱一些的 Learner，去学习它的预测残差，不断修正预测结果。

也正因为此，当我们从 $M$ 棵 Boosting 树中最终得到了新输入样本时，我们计算得到了它的 $\log (\text{odds})$，只需要加上 sigmoid 变换成最终的概率，就可以了。

总结：GBDT 分类 vs. 回归⚓︎

特性	GBDT for Regression	GBDT for Classification (Binary)
核心问题	预测一个连续值	预测一个离散类别（通过概率）
损失函数	均方误差 (MSE)	对数损失 (Log-Loss) / 二项偏差
初始化 $F_0(x)$	所有样本标签的均值	所有样本标签的对数几率 (log-odds)
伪残差 $r_{im}$	真实值 - 预测值 ($y_i - F_{m-1}(x_i)$)	真实值 - 预测概率 ($y_i - p_{i, m-1}$)
弱学习器 $h_m(x)$	回归树，拟合残差	回归树，拟合残差
叶子节点输出 $\gamma_{jm}$	区域内残差的均值	区域内残差/二阶信息的一个比值
最终预测	直接输出 $F_M(x)$	先计算 $F_M(x)$，再通过 Sigmoid 转换为概率

总而言之，GBDT 做分类是通过巧妙地替换损失函数，将问题转化为了在梯度指导下的一系列回归问题。它的框架非常灵活，这也是 GBDT 如此强大的原因之一。

MSE 与 Cross Entropy 的辨析⚓︎

可以发现，一般 MSE 用于回归，而交叉熵（或者二分类的 Log Loss）用于分类，这是为什么？为什么不把 MSE 用在分类？

本质上，MSE 衡量的是连续值之间的距离，而 CE 衡量的是概率分布之间的距离，本质属于极大似然估计，试图最小化预测分布和真实分布之间的差异。

在梯度上，交叉熵的梯度更新效率更高，$(\hat{y} - y)$，而如果是MSE，最后用sigmoid将输出映射到 [0, 1] 区间时，容易导致梯度消失（以逻辑回归为例）。因为sigmoid求导， $\hat{y} (1 - \hat{y})$.

在函数性质上， MSE 会导致 logistic 回归任务中函数是非凸的，容易陷入局部最优。

最后，交叉熵的计算效率更高。