广义线性回归：T-test与ANOVA分析⚓︎

约 1751 个字 9 张图片预计阅读时间 6 分钟

The goal of t-test is to compare means and see if they are significantly different from each other.

我们首先考虑简单的情况。我们有两种类别，每一个类别有多个样本，每个样本都有一个指标的具体值。比如我们有两组小鼠，一组突变一组没有突变，我们分别记录这两组中所有小鼠的体重。

Follow LR steps: (which is very very important!)

Find the overall mean;
Calculate SS(mean). 基于多类的数据计算全部数据的SS。
Fit a line to the data.

在对数据进行fit的时候有不同：对不同种类的数据，每一个类都分别取mean。但是回忆LR，我们只fit出了一条线，现在有多条，怎么用一个公式表示这些线呢？

有一种将两条线合并成一个单一等式的方法。采取这种方法后，后续步骤会与F检验完全相同。

我们开始。

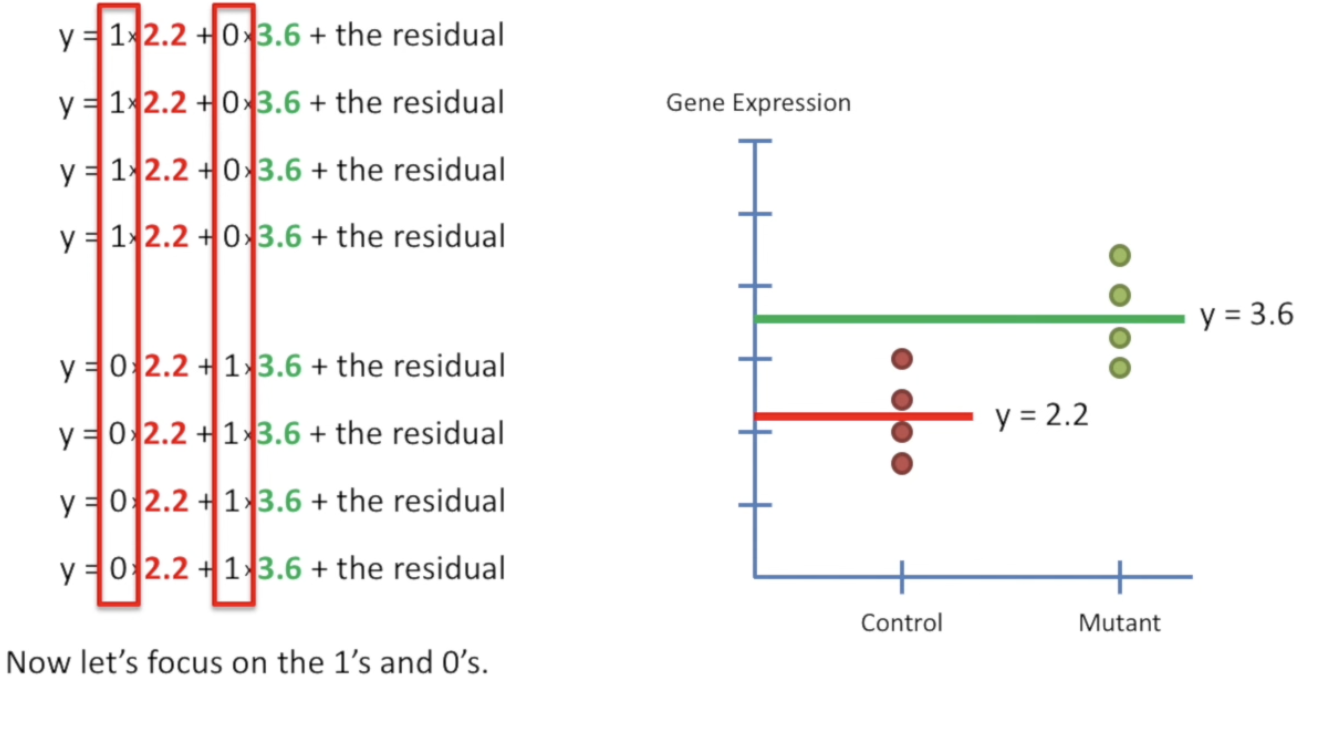
我们可以form 一个矩阵：Design Matrix。这里的0-1就像是开关，决定了每个类的mean是否“开/关”。

我们可以用公式 \(y = MEAN_{type_A} + MEAN_{type_B}\) 来进行表示。这样的话，相当于我们有 \(2\) 个参数来表示这个公式。

计算SS(fit)，也就是拟合后结果的SS。

这样，我们公式：

\[F = \dfrac{[SS(mean) - SS(fit)] / (p_{fit} - p_{mean})}{SS(fit) / (n - p_{fit})}\]

就可以照搬自LR的结果了。我们把两种情况进行对比。会发现，T-test更加侧重于“类别”，即样本中多个类在某个指标变化的情况。

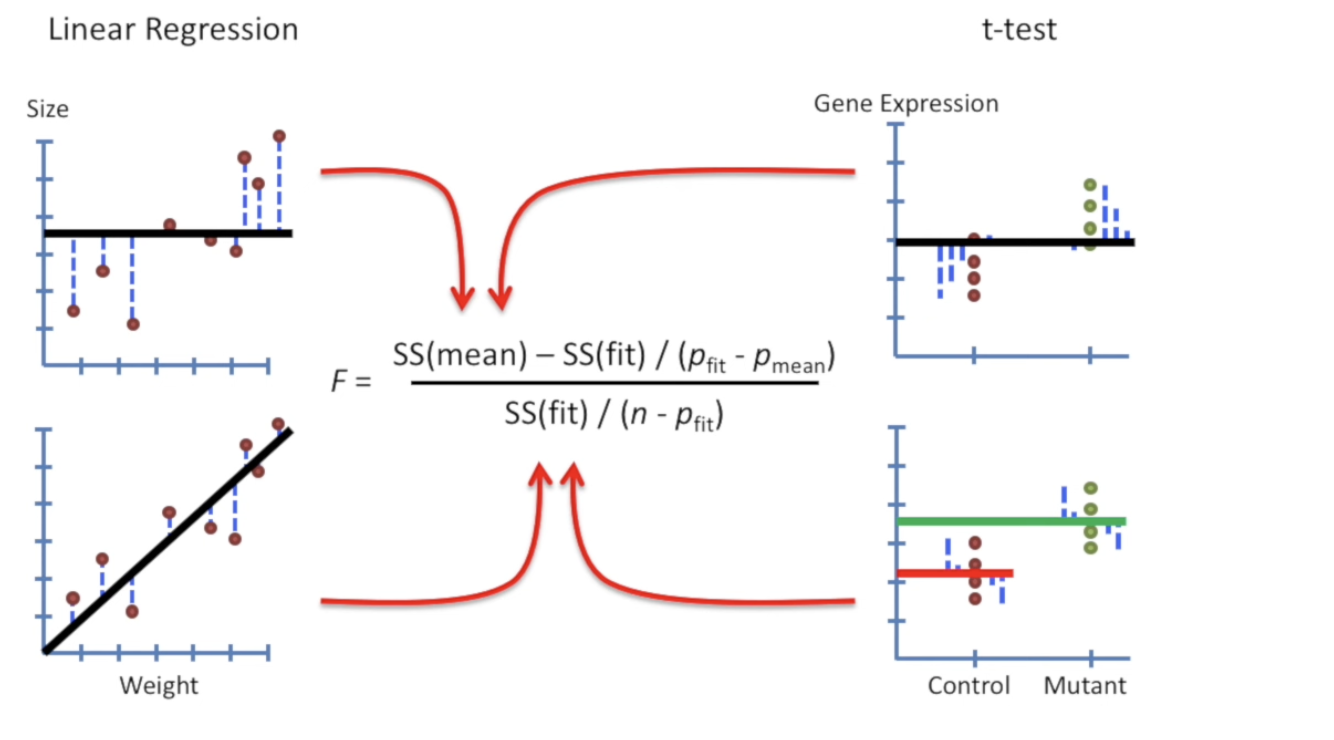
注意了，在如上的 T-test 的场景下，\(p_{mean} = 1, p_{fit} = 2\)

ANOVA⚓︎

我们把刚才的情况扩展到5种类别，ANOVA就在此出现了。ANOVA可以探讨这多种类别样本在某一个固定指标上是否是相同的。

照搬上面的操作即可。此时我们需要做一个有5组不同0-1的长长的矩阵。如图所示。分别表示5个类别情况下的不同。

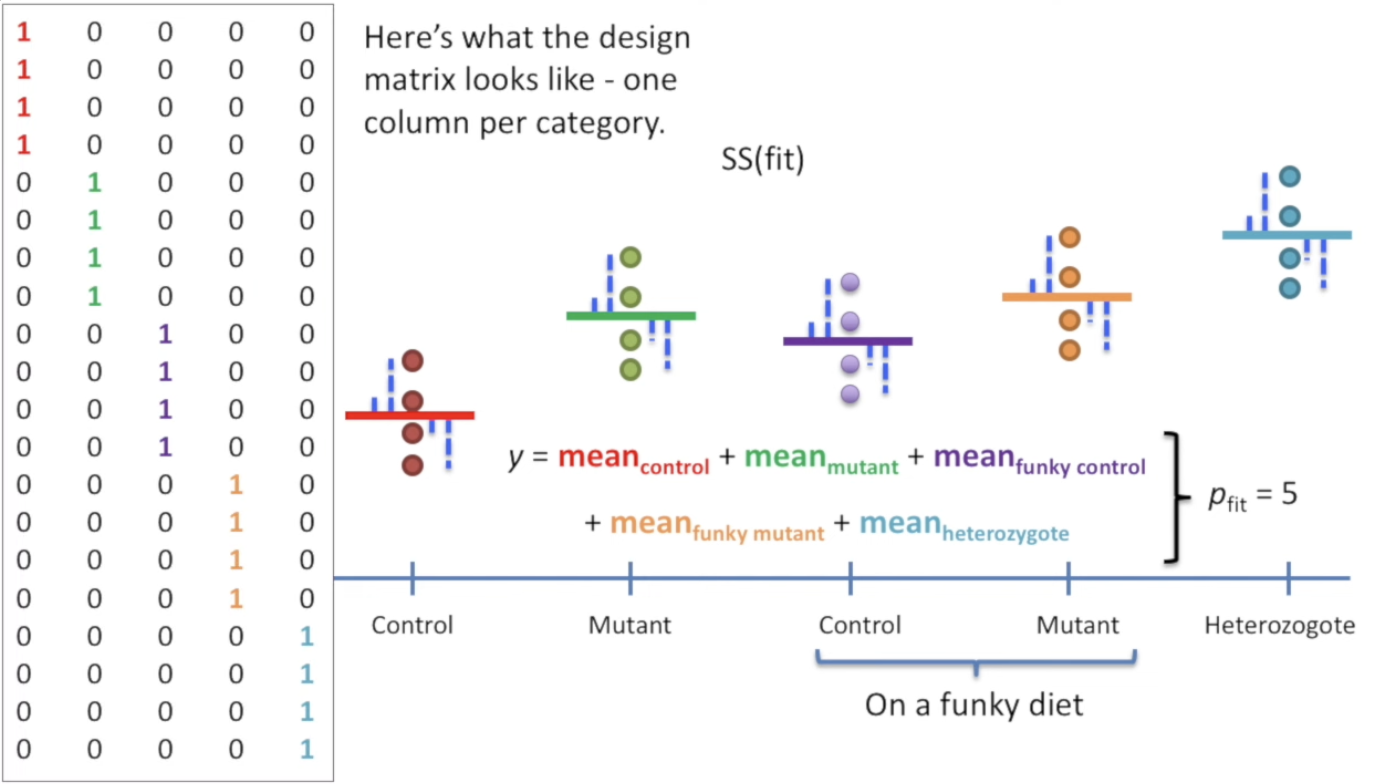
我们刚刚使用的design matrix（就是用来表征每个类是否被选中的那个矩阵），在标准的计算中会被写成如下新的样式，即第一列全是1，后面按组别变化。

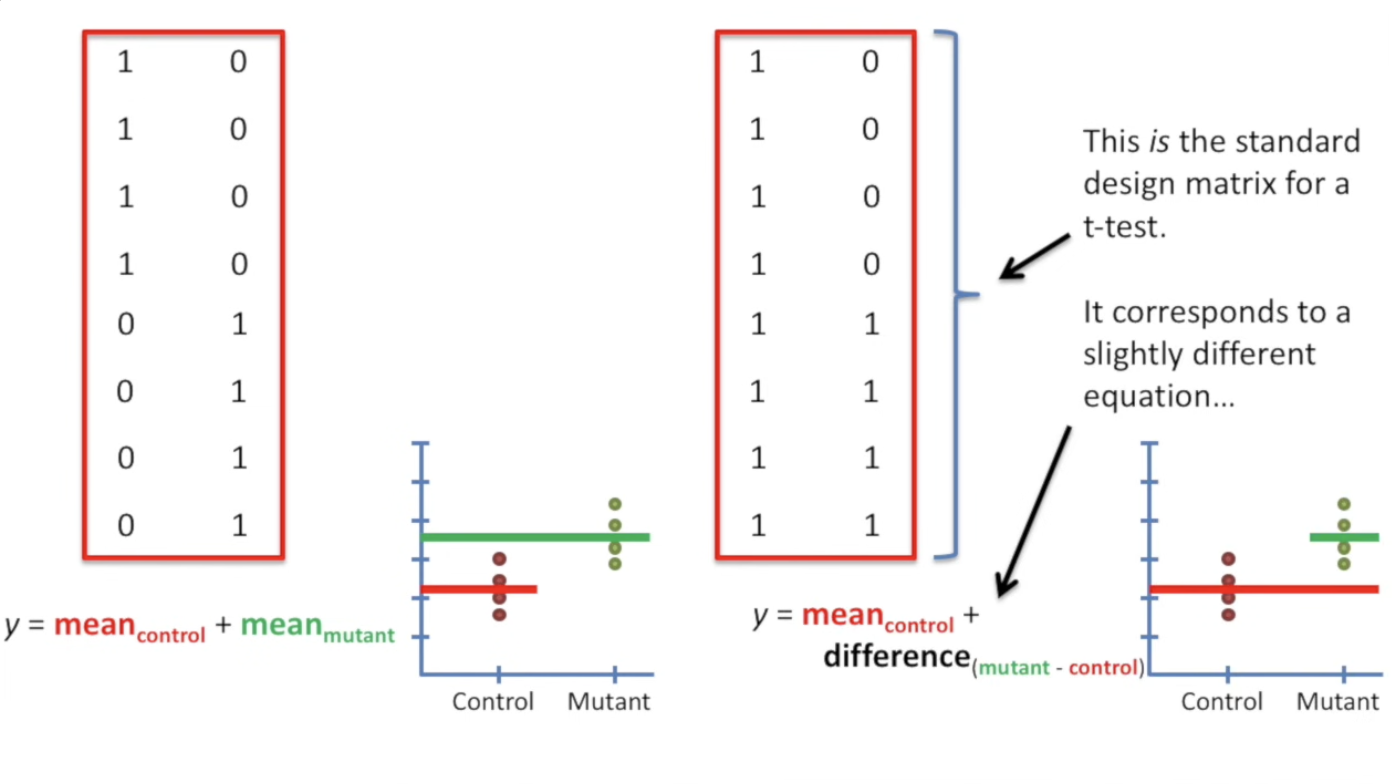
为什么？参考下面解释：

Design Matrices⚓︎

为什么标准的T-test矩阵是：上图右边所示，而不是左边？

这个新公式的含义是：

\[y = 1 \times MEAN_{Type_1} + 0 \times diff(Type_1 - Type_2)\]

第一列是要与 \(MEAN_{type_1}\) 相乘，第二列意味着要与 Type1 与 Type 2 均值的差相乘。

两种矩阵表达的残差是相同的。\(p_{fit}\) 也是相同的，同样数据得到的 \(p-value\) 也是相同的。那为什么要用右边的呢？

对于那些全是0/1的matrix，很适合做T-test，或者ANOVA，适合处理那些不同类别(categories)的数据，但是我们也可以用其他的数字。

举个例子

我们以线性回归为例，假设我们的公式是：

y = y-intercept + slope

我们的第一列的元素需要和 y-intercept 相乘，第二列的元素需要和 slope 相乘。

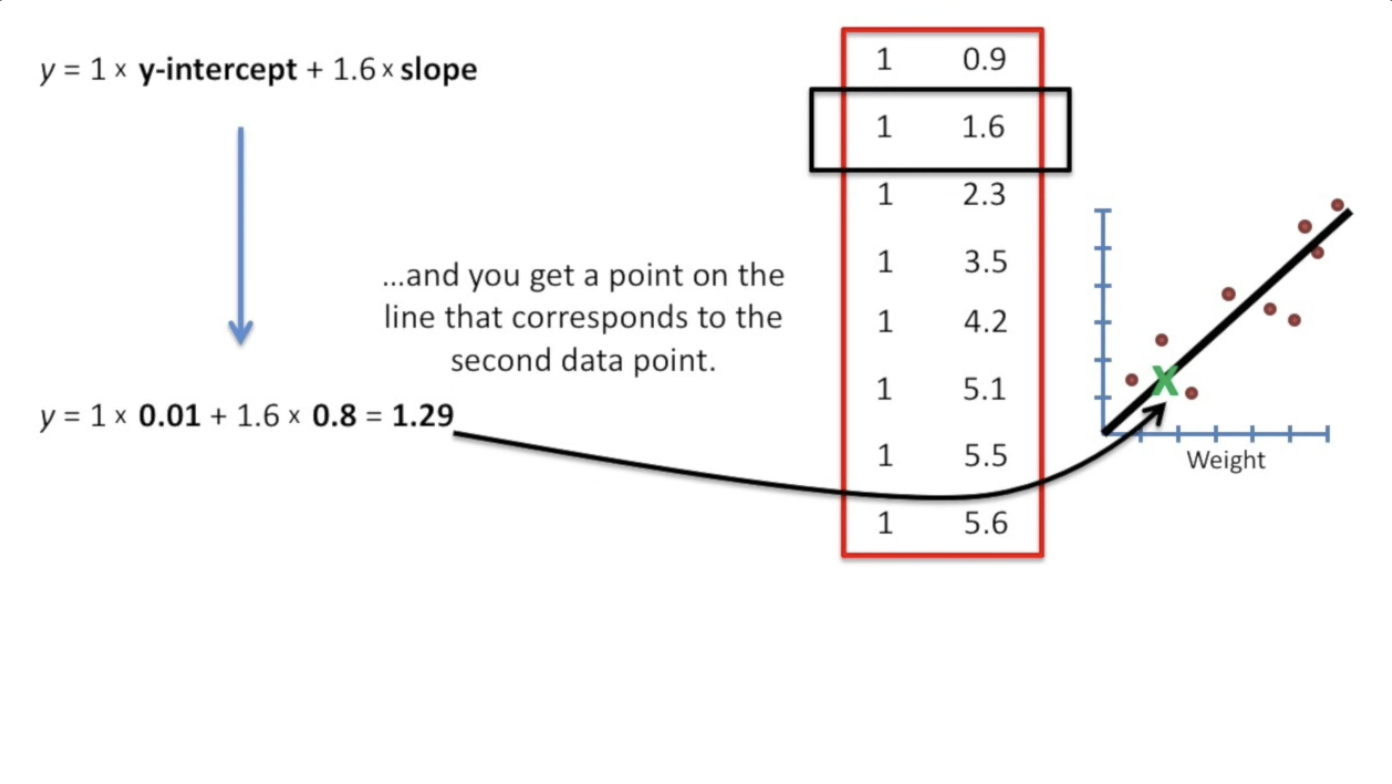
此时，我们引入第二列为实数（其实也就是我们的自变量在数据中的值），第一列均为1.

会发现，这个矩阵的数字对应到上面那个y的公式，乘下来的结果正好就是拟合直线上的点。

在这种“第一列都是1”的design matrix下，我们不止可以加入0或者1，我们可以加入==任何实数== ，只要我们设置好了 \(y\) 的表达式含义。这样，我们只需要把矩阵对应位置塞上需要的数，这个矩阵与我们的拟合曲线的参数的向量相乘，就“通过数据中的自变量找到了拟合曲线对应的点”，这有助于在表达式中刻画拟合线/面的情况。

我们可以把T-test和回归结合起来 ...

比如如下的复杂情况：有两种老鼠，他们各自有自己的size-weight关系。我们能否用统计方法来检验这两种老鼠之间是否有显著的不同呢？

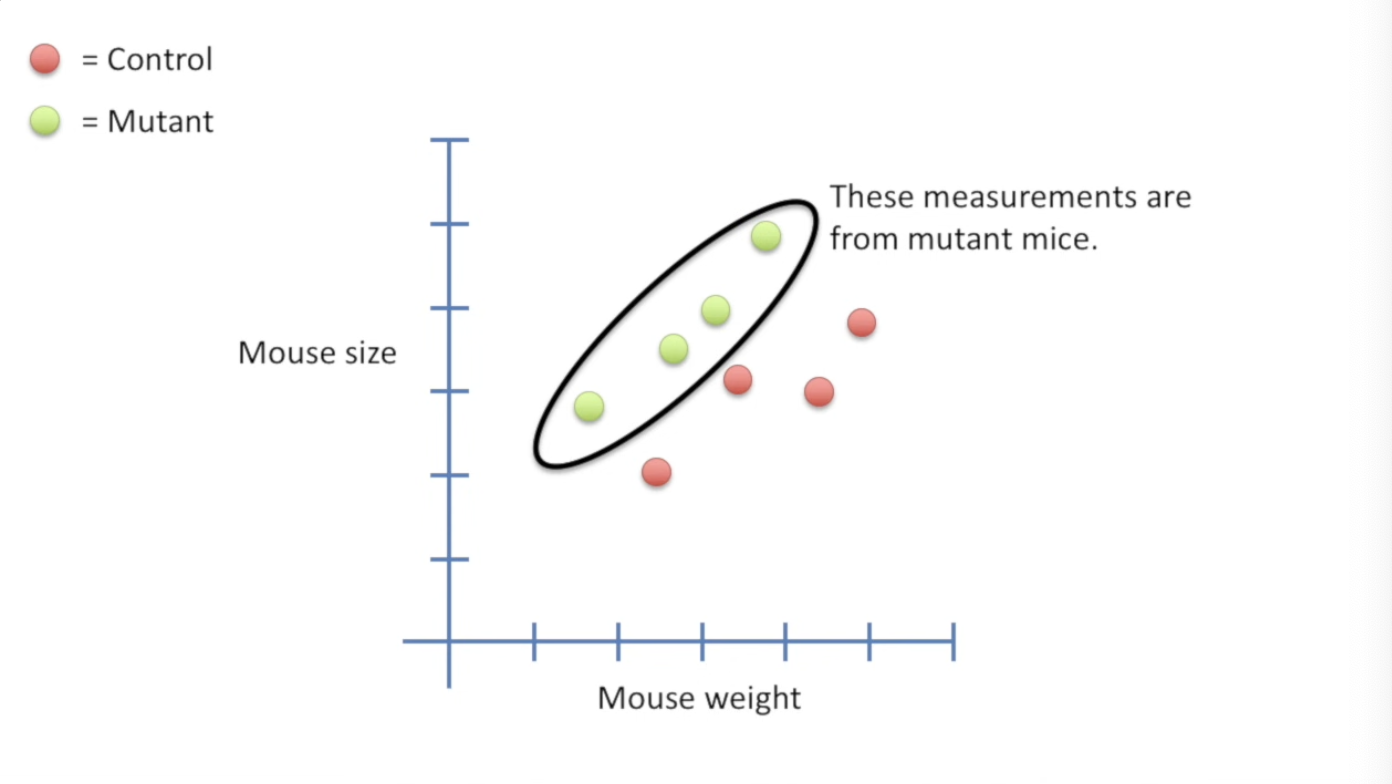
相比T-test，我们依然有两种类别，每一个类别有多个样本，但是每个样本有多个指标，比如我们有两组小鼠，一组突变一组没有突变，我们分别记录这两组中所有小鼠的体重以及大小。

如果我们仅仅用regression，我们只会从总体中获得一个fit line；如果我们仅仅用T-test，我们仅仅能获得在不同类别的某一个指标上二者的差异等（还不一定显著）。

我们想要比较的是，既能比较多个类别，又能表示fit-line！所以！Combine T-test and Regression!!!

怎么做呢？如下图，注意一下我们的 \(y\) 的公式（我们默认两个线的slope相等）。我们把矩阵的最后一列用x轴填充，因为这加上 control-intercept 正好就是control的红线；而第二列则负责表示mutant造成的偏移，只在绿线的时候才取到。

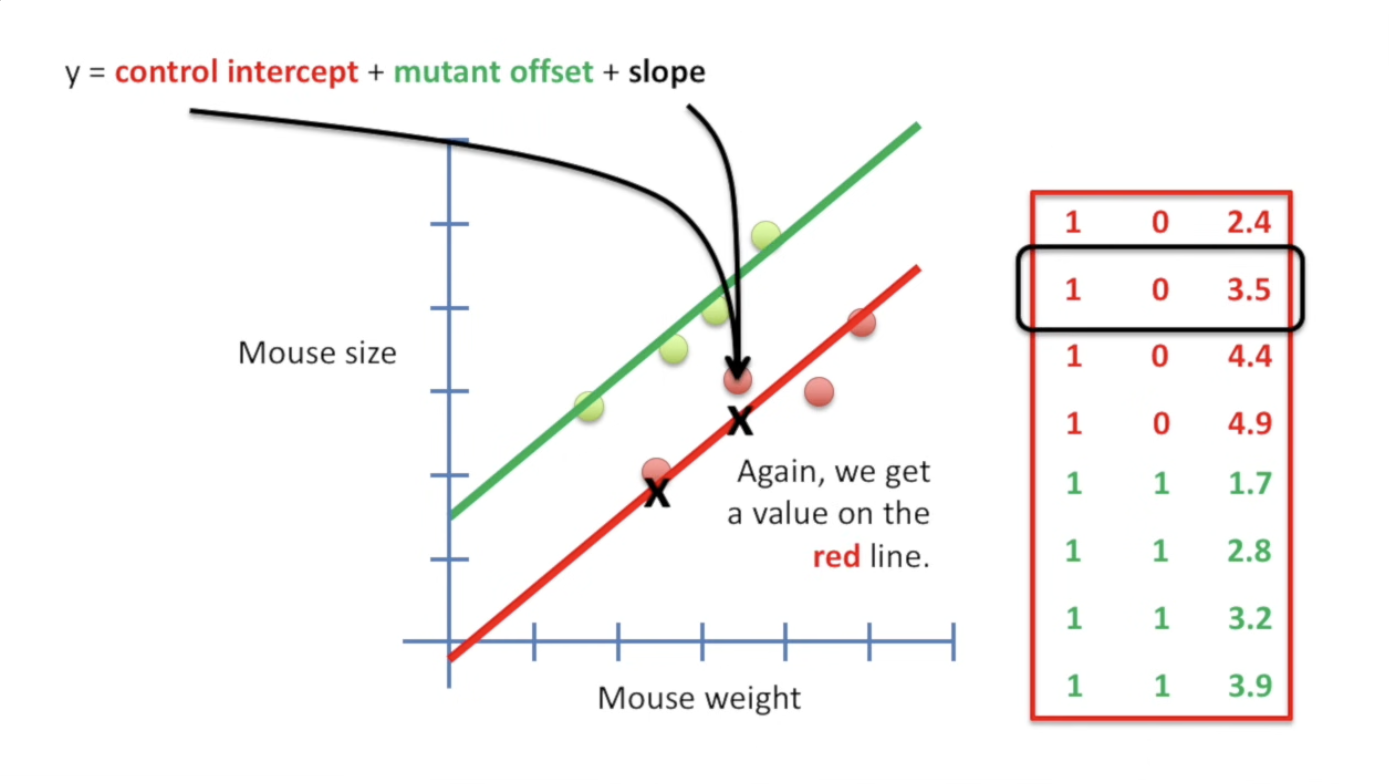
这个矩阵的每一行，都需要和那个 y 的表达式乘起来才可以表示一个具体的点！这个矩阵的作用，就是保证乘完之后的结果，能够表征我们的数据。每一行，对应一个数据！

如果我们想要表示： y = intrcept_1 + offset + slope_1 + slope_2，也就说斜率不同的情况，怎么办呐？

Here we go~

\[\begin{bmatrix} 1 & 0 &a_1 & 0 \\ 1 & 0 &a_2 & 0 \\ 1 & 0 &a_3 & 0 \\ 1 & 0 &a_4 & 0 \\ 1 & 0 & 1 & b_1 \\ 1 & 0 &1 & b_2 \\ 1 & 0 &1 & b_3 \\ 1 & 0 &1 & b_4 \\  \end{bmatrix}\]

我们用这种新方法对这两个数据进行fit，然后用F检验进行检查，会发现一个较小的p-value，说明，同时考虑样本中不同类的子样本，以及子样本的一个变量进行预测，比仅仅使用一个type的均值进行预测的simple model，效果要显著地好。

当然了，你可以和其他的simple model对比，比如：考虑所有样本进行的线性回归，不考虑样本的类别；比如，仅仅考虑样本不同类别对一个指标进行T-test的预测。

公式里的 \(p_{fancy}\) 就是3，对应新模型的3个参数。

最后一个例子⚓︎

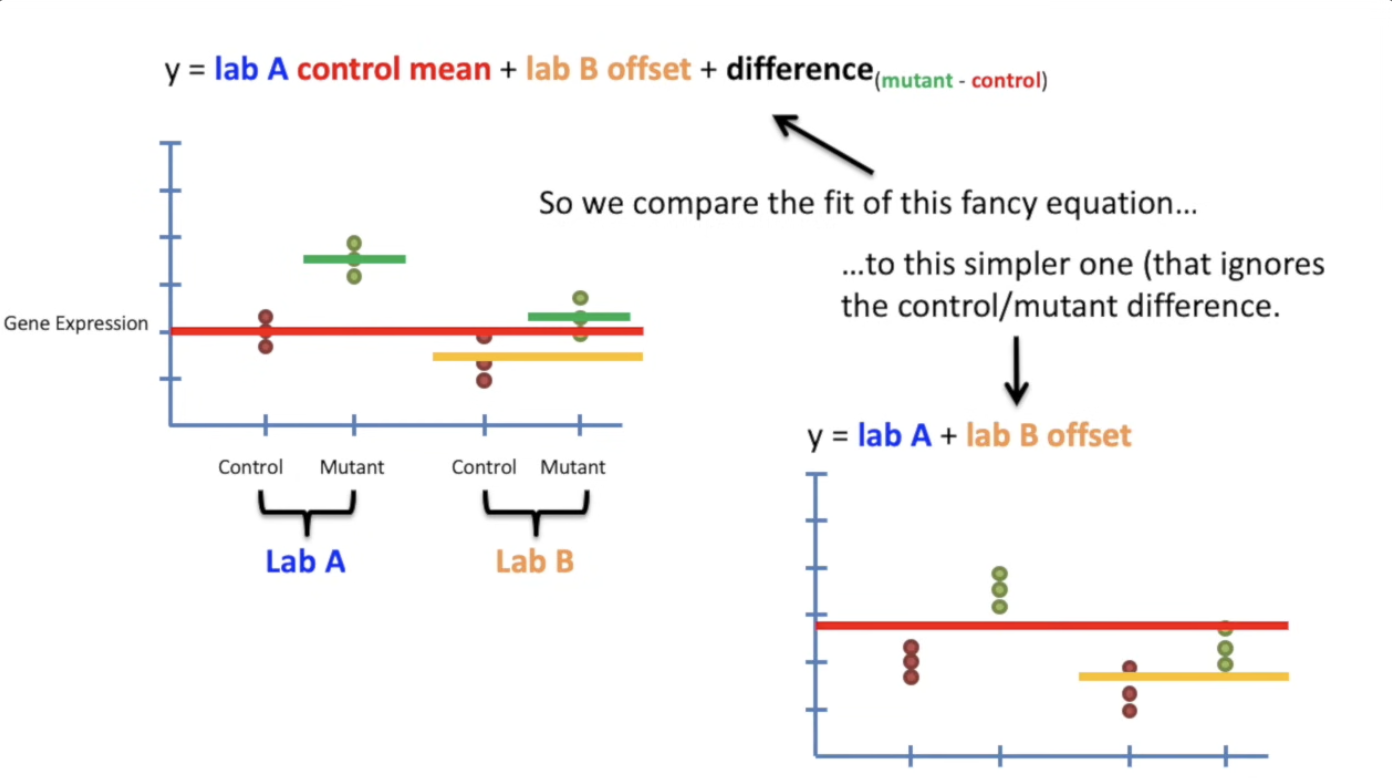
如果有两个实验室同时重复了实验，但是得出的结果有偏差，（batch-effect），我们该如何补偿呢？

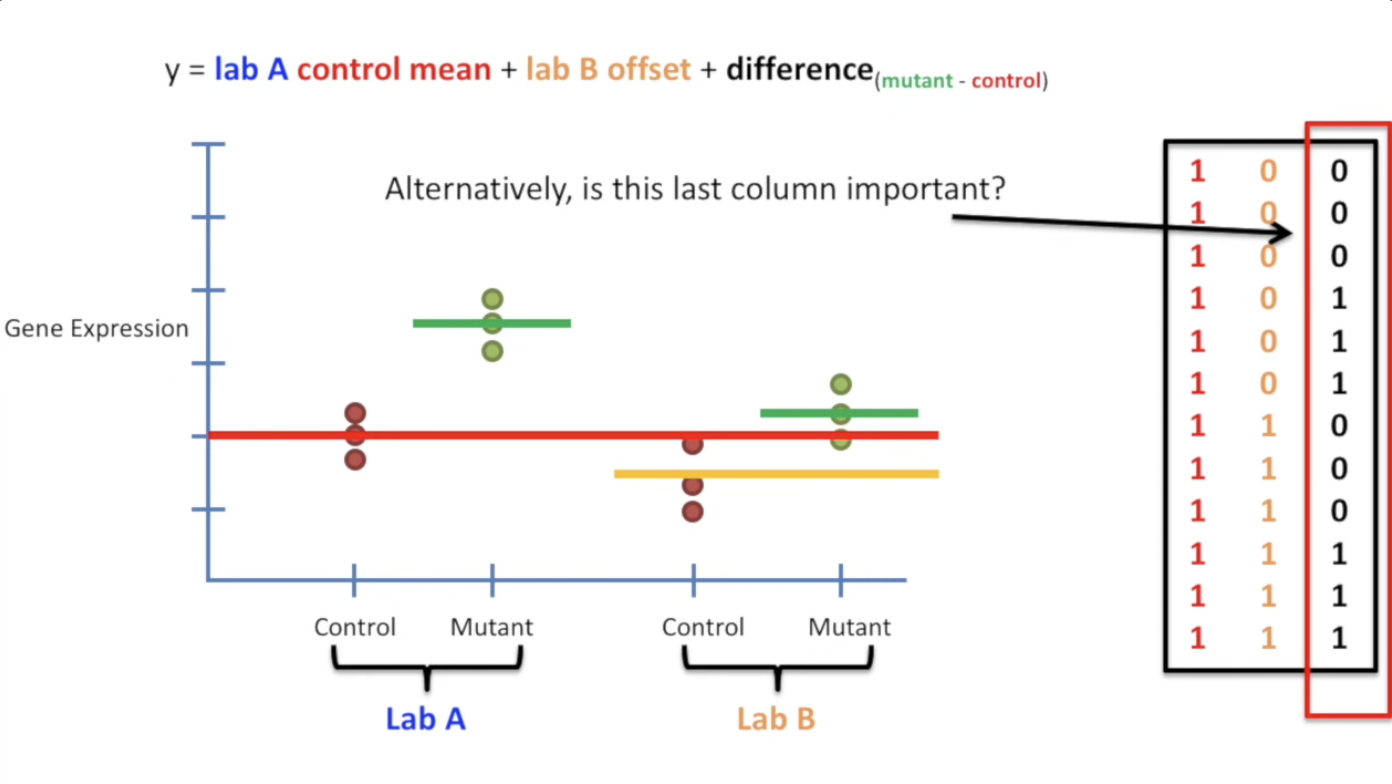
或许我们可以总结，如果要处理category的不一样，需要在 y 中加入 \(differece(type_a - Type_b)\)，而如果是其他指标，同样需要随机应变。

同样地，为了验证加上最后一列是否有必要，我们还可以继续和 simple model 进行对比：