多层感知机 (MLP)⚓︎
约 1790 个字 1 张图片 预计阅读时间 6 分钟 总阅读量 次
多层感知机(Multi-Layer Perceptron, MLP)是深度学习和神经网络领域最基础、最核心的模型之一。它本质上是前馈神经网络(Feed-Forward Neural Network)的一种经典形式。
MLP可以被理解为对逻辑回归(或单层感知机)的扩展。逻辑回归只有一个计算层,只能学习线性决策边界。MLP通过堆叠多个“层”,并引入非线性激活函数,从而获得了学习和表示极其复杂的非线性关系的能力。
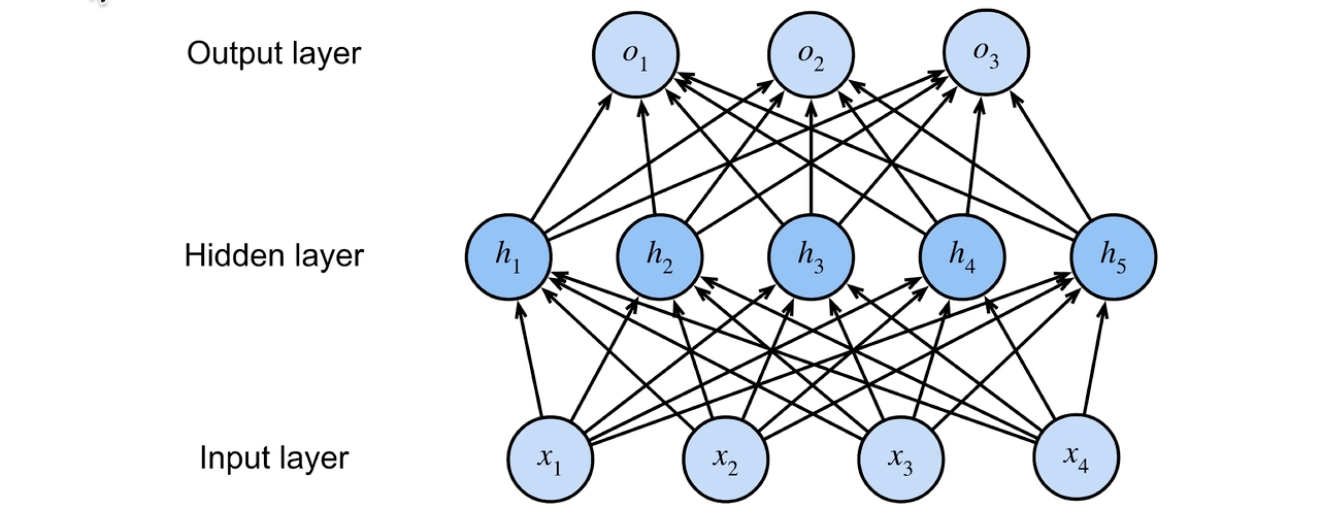
1. MLP 流程 / 解决的问题 / 应用场景⚓︎
- 输入 \(x \in \mathbb{R}^{n}\),要解决一个 \(k\) 分类的问题,输出向量长度为\(k\)。
- 单隐藏层 \(W_{1} \in \mathbb{R}^{m \times n}\),\(b_{1} \in \mathbb{R}^{m}\)
- 输出层 \(W_{2} \in \mathbb{R}^{m \times k}\),\(b_{2} \in \mathbb{R}^{k}\)
\[\mathbf{h} =\sigma\left ( W_{1} \mathbf{x} + B_{1} \right )\]
\[o = W_{2}^{T} \mathbf{h} + B_{2}\]
其中\(\sigma\)为激活函数。Element-wise 进行计算。一般用 sigmoid.\(f(x) = 1 / (1 + \exp(-x))\)。参考 我的 Activition Function 笔记。
为什么需要激活函数?为什么需要非线性?
如果不激活,那么\(W^T_2 (W_1 x + B)\)本质上还是线性函数,是简单的矩阵乘法的结果。
而,为了在分类时从更加丰富、非线性的方式对数据特征进行表示,可以增强模型的分类能力。是十分有必要的。
MLP是一个强大的通用函数逼近器(Universal Function Approximator)。理论上,一个具有足够多神经元的单隐藏层 MLP,能够以任意精度逼近任何连续函数。这使得它能够解决两大核心问题:
-
非线性分类(Non-linear Classification):当数据的决策边界不是一条直线(或一个平面)时,MLP可以学习到任意形状的复杂边界。这包括二分类、多分类和多标签分类。经典的 “XOR异或问题” 就是一个线性分类器无法解决,但MLP可以轻松解决的例子。
对于多分类问题,有 K 个类则最后一层就输出 K 个值(这个值就是logits,注意,softmax 的输入才是 logits。
K 个值做 softmax 就可以得到对应概率了。
-
回归(Regression):预测一个或多个连续值。MLP可以学习输入特征与连续输出之间的非线性映射关系。
当然不要忘了你可以一直增加隐藏层,每个隐藏层可不同数量的神经元。如果MLP比较深的话,最好从顶到下的层数慢慢减小,并且第一个隐藏层不能过大。因为本质上 MLP 是一个数据压缩的过程,把数据压缩到类别。因此需要注意其大小变化。
2. 训练过程⚓︎
MLP的训练过程依赖于反向传播(Backpropagation)算法和基于梯度的优化方法(如梯度下降)。整个流程可以分为四个核心步骤,在一个循环中不断重复(这个循环被称为训练)。
假设我们有一个输入层、一个隐藏层、一个输出层的MLP。
训练准备: 1. 定义网络架构:确定有多少个隐藏层,每个隐藏层有多少个神经元,以及选择什么样的激活函数(如ReLU, Sigmoid, Tanh)。 2. 初始化参数:随机初始化网络中所有的权重(Weights,\(W\))和偏置(Biases,\(b\))。不能初始化为0,否则会导致对称性问题,使网络学不到东西。
核心训练循环(对一批数据进行一次迭代):
第1步:前向传播 (Forward Propagation)
数据从输入层开始,逐层向前计算,直到输出层,得到预测结果。 * 对于隐藏层中的每个神经元,计算: 1. 线性组合:\(z = W \cdot (\text{上一层的输出}) + b\) 2. 非线性激活:\(a = g(z)\),其中\(g\)是激活函数(如ReLU)。 * 这一层的输出 \(a\) 将作为下一层的输入。 * 最后,输出层得到最终的预测值 \(\hat{y}\)。
第2步:计算损失 (Calculate Loss)
将模型的预测值 \(\hat{y}\) 与真实的标签 \(y\) 进行比较,计算它们之间的差距。这个差距由损失函数(Loss Function)来量化。 * 分类问题:常用交叉熵损失 (Cross-Entropy Loss)。 * 回归问题:常用均方误差 (Mean Squared Error, MSE)。
第3步:反向传播 (Backward Propagation)
这是训练的核心。该算法基于微积分中的链式法则,计算损失函数对网络中每一个权重\(W\)和偏置\(b\)的梯度(偏导数),即\(\frac{\partial L}{\partial W}\)和\(\frac{\partial L}{\partial b}\)。 * 这个过程从输出层开始,将“误差”逐层向后传递。 * 每一层利用后一层传回的梯度,计算当前层的梯度,并继续向前传递。 * 它告诉我们每个参数应该朝哪个方向调整,才能使损失变得更小。
第4步:更新参数 (Update Parameters)
根据计算出的梯度,使用一个优化器(Optimizer)来更新网络的所有权重和偏置。 * 最简单的更新法则是随机梯度下降(SGD):
\[W_{\text{new}} = W_{\text{old}} - \eta \cdot \frac{\partial L}{\partial W}\]
\[b_{\text{new}} = b_{\text{old}} - \eta \cdot \frac{\partial L}{\partial b}\]
其中\(\eta\)是学习率(Learning Rate),控制每次更新的步长。
- 现代实践中更常用Adam、RMSprop等更高级的优化器,它们能自适应地调整学习率。
重复:对数据集中所有的批次(batch)重复以上四步,完成一轮完整的训练(称为一个 epoch)。通常需要训练多个 epoch,直到模型的损失不再显著下降。
3. 算法复杂度⚓︎
MLP的复杂度主要取决于网络的参数数量(即权重和偏置的总数)。
令\(L\)为网络层数,\(n_l\)为第\(l\)层的神经元数量(\(n_0\)是输入特征维度)。 * 第\(l\)层的权重矩阵大小为\(n_l \times n_{l-1}\)。 * 第\(l\)层的偏置向量大小为\(n_l\)。
训练复杂度 (单次更新)
- 前向传播:主要开销是矩阵乘法。对于一层,复杂度约为 \(O(n_l \cdot n_{l-1})\)。整个网络的前向传播复杂度约为 \(\sum_{l=1}^{L} O(n_l \cdot n_{l-1})\) 。如果使用批处理(batch size为B),则乘以B。
- 反向传播:计算量与前向传播在同一个数量级。
- 总训练复杂度:大致与参数数量成正比。与SVM的\(O(N^2)\)不同,MLP的训练复杂度对样本数量\(N\)是线性的(因为我们是分批次处理的),但对网络规模(宽度和深度)是多项式级的。这使得MLP能很好地扩展到非常大的数据集上。
推理(预测)复杂度 (单个样本)
- 推理过程只需要进行一次前向传播,不涉及反向传播和参数更新。
- 复杂度约为 \(O(\sum_{l=1}^{L} n_l \cdot n_{l-1})\),即与参数数量成正比。
- 这个过程非常快,因为主要是高度并行化的矩阵运算,适合部署到需要实时响应的在线服务中。