从朴素贝叶斯到Gaussian Naive Baysian⚓︎

约 1866 个字 3 张图片预计阅读时间 6 分钟

朴素贝叶斯⚓︎

一个有意思的问题

Likelihood 和 Probability 之间是什么区别？

快速入门案例：垃圾邮件分类⚓︎

我们有一些分类好的数据。其中一部分是正常邮件(Normal)，一部分是垃圾邮件(Spam)。我们需要从这些已有的内容中，使用某种方法，使得收到新邮件时，能自动筛选出垃圾邮件。

第一件事

我们可以根据正常邮件中所有出现的单词，制作一个单词频数直方图。比如：Dear / Friend / Lunch / Money (8 / 5 / 3 / 1) 在正常邮件里出现的频率。也就是 ( 8 / 17 ) / ( 5 / 17 ) / ( 3 / 17 ) / ( 1 / 17 )。也就是: 0.47， 0.29， 0.18，0.06. 这就是 \(P( \text{Dear} | N), P( \text{Friend} | N )\)，以此类推。

同样，我们可以制作一个垃圾邮件中所有单词的频数直方图。比如： Dear / Friend / Lunch / Money (2 / 1 / 0 / 4)。计算频率：（0.29 / 0.14 / 0 / 0.57）。这就是 \(P( \text{Dear} | S), P( \text{Friend} | S )\)，以此类推。

第二件事

我们现在收到一封新邮件，内容是：Dear Friend。我们需要计算这封邮件是正常邮件的概率，和是垃圾邮件的概率。也就是 \(P(N | \text{Dear Friend})\) 和 \(P(S | \text{Dear Friend})\)。

我们首先要算的是：不管写什么，这个邮件是正常邮件的概率，也就是 \(P(N)\)。这个只能根据我们的训练集计算。比如，我们有8个正常邮件，4个垃圾邮件。我们的 \(P(N) = 8 /12, P(S) = 4/ 12\)。这个就是先验概率。

现在，我们把这个正常邮件的概率，乘上“这封新邮件中的每个字在正常邮件中出现的概率： \(P(N) \times P( \text{Dear} | N) \times P( \text{Friend} | N) = 0.09\)。这个值可以视为正比于 \(P( N | \text{Dear Friend} )\)

同理，我们也可以根据“邮件是垃圾邮件的概率”，乘以“这封新邮件中的每个字在垃圾邮件中出现的概率”。\(P(S) \times P( \text{Dear} | S) \times P( \text{Friend} | S) = 0.01\)。这个值可以视为正比于 \(P( S | \text{Dear Friend} )\)

思考：这里可以直接相乘，意味着什么？

第三件事

对比可以发现，我们可以决策：\(0.09 > 0.01\)。这个邮件是个正常邮件。

However... 下面我们看一个进阶的例子。

依然是上述训练数据。但是我们需要判断的新邮件是： "Lunch Money Money Money Money"。

按照道理说，Money在垃圾邮件中出现的频率较高，应该会预测成“Spam” ... 吧？

但是，计算一下就会发现，\(P(S) \times P( \text{Lunch} | S) \times P( \text{Money} | S)^4\) 始终为0。因为 Lunch 没有出现在垃圾邮件词表中。但是，由于Lunch出现在了Normal 词表中，所以，正常邮件的预测概率，不为0。我们就会把它判定为正常邮件。

为了解决这个情况，通常的做法是在每个词上都加一个（或者多个）记数，记为 \(\alpha\)。确保在垃圾和正常邮件的数据中，不会有某个字的频数是0。

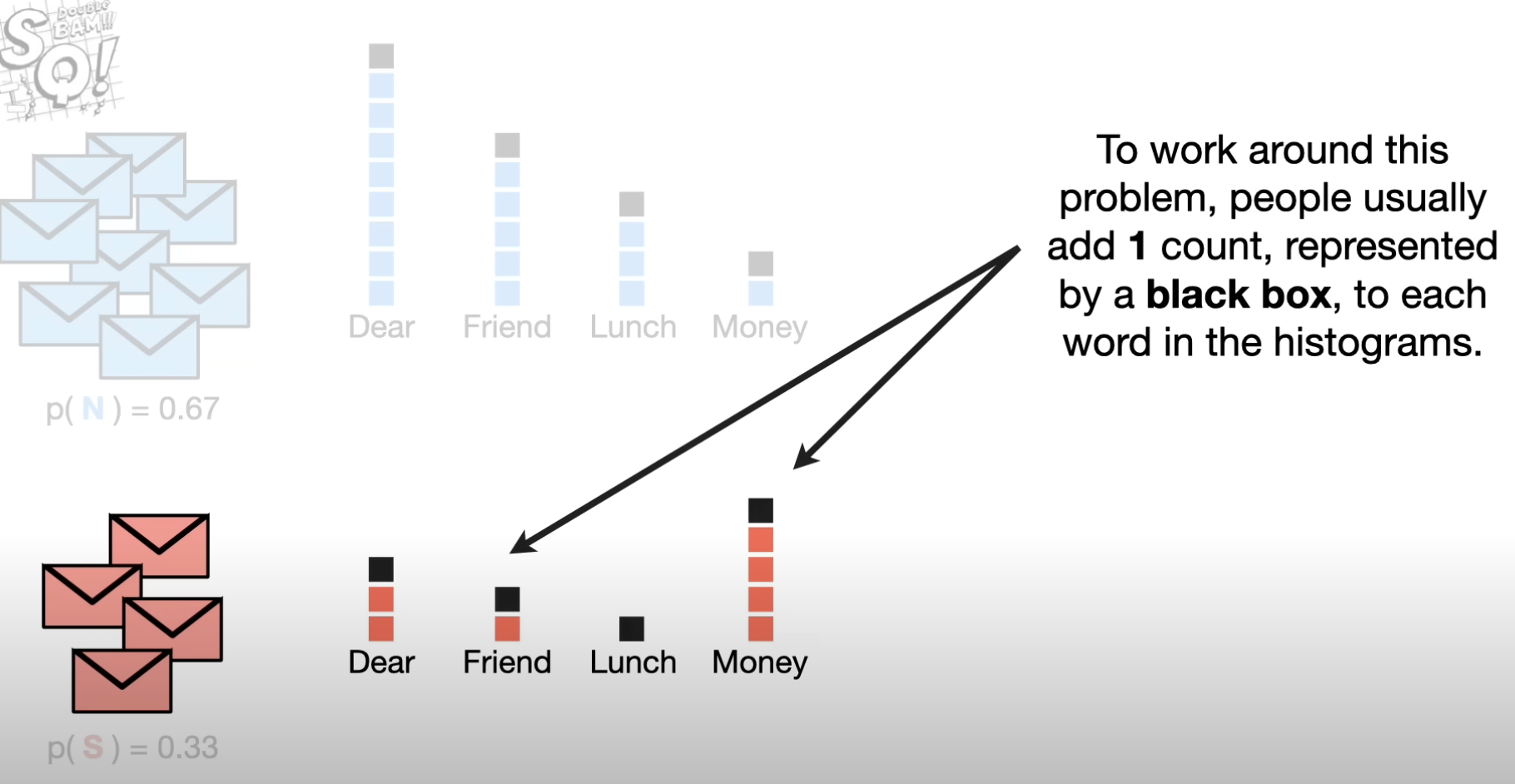
这样，我们的每个单词在特定集合中的出现频率也就要改改了。以垃圾邮件对应的先验的词频而言，Dear / Friend / Lunch / Money (3 / 2 / 1 / 5)。计算频率：（0.27 / 0.18 / 0.09 / 0.45）。这就是 \(P( \text{Dear} | S), P( \text{Friend} | S )\)。

这下，我们就可以在新的概率下，重新计算上面的“第二件事”所做的内容了。可以算出 \(P(N) \times P(\text{Lunch} | N) \times P(\text{Money} | N)^4\)。我们也就可以正常识别了！

为什么Naive Bayesian 是Naive的

以上面的例子为例。它默认了不考虑单词的出现顺序，而把每一段文本视作一些词袋。

However，在垃圾邮件分类上，确实有不错的效果。

Gaussian Naive Bayesian⚓︎

快速入门案例：预测观众喜好⚓︎

我们现在有一些训练数据：一些人对于电影Troll2是否喜欢：Yes or No，以及每个人的一些额外信息 (Popcorn, Soda, Candy的摄入量)。我们需要训练模型，从这些已有的内容中，使用某种方法，使得知道一个人的类似的额外信息的数值，就可以判断出ta是否喜欢电影Troll 2。

第一件事: 对于喜欢和不喜欢的人，我们都可以算出这个群体某个指标的统计量，比如 Mean 和 Standard Deviation。我们根据这两个统计量构成正态分布（高斯分布），绘制分布图。我们把这两个群体的分布可视化，也就是：

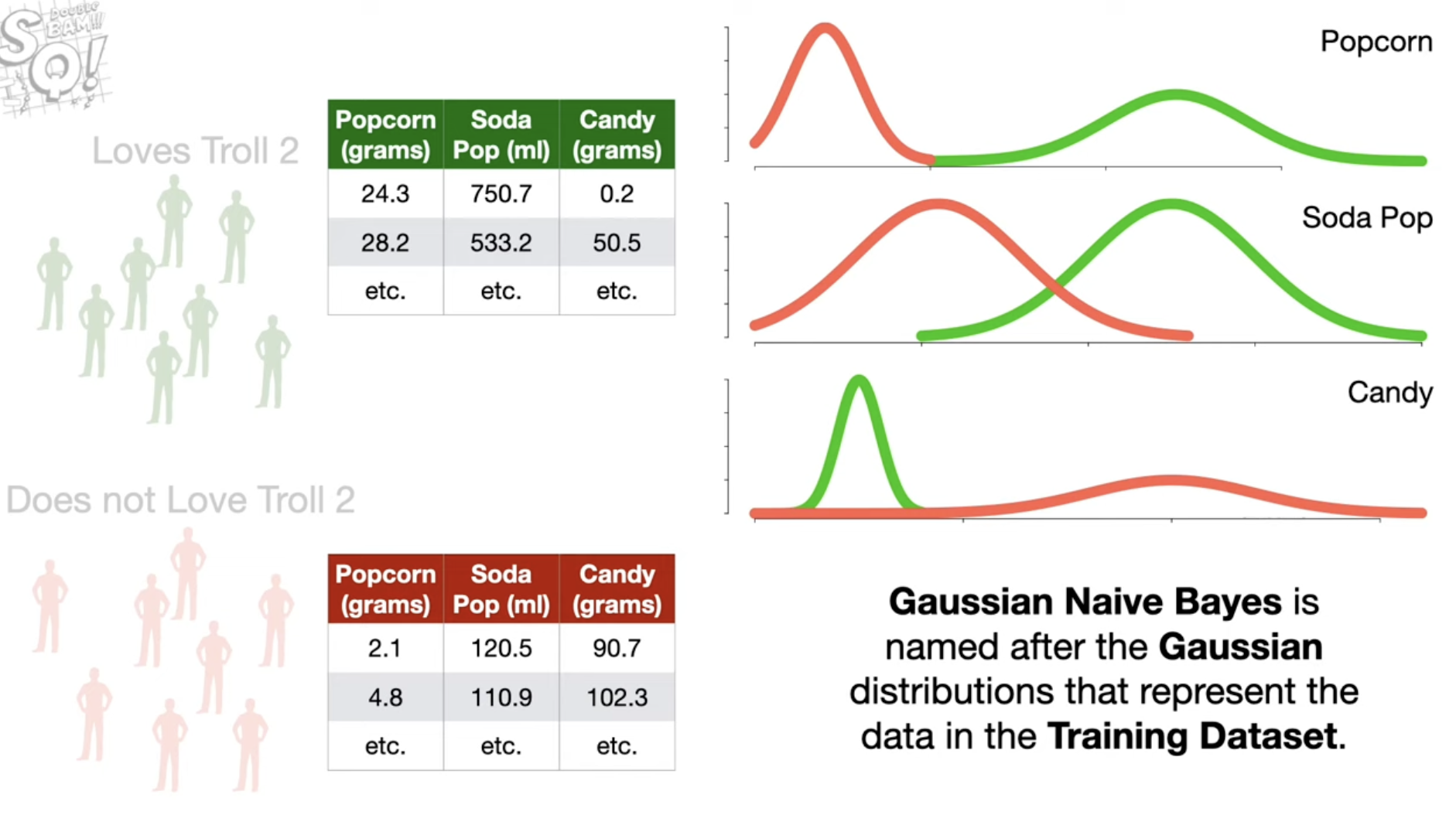
第二件事

我们现在收到一个新观众的信息。比如ta的三个指标分别为 \((20, 500, 25)\)。我们要用Gaussian NB来判断ta的喜好。首先，我们要做一个Initial Guess. 我们根据训练集中Love / Not Love的比例，算出 \(P(L)\) 和 \(P(N)\)，这是先验概率。

接下来，需要根据正态分布，计算出：在知道了喜好的情况下，ta的某个指标是某值的 Likelihood。比如： \(P( \text{Popcorn} = 20 | L)\)，就是要在正态分布那个概率密度图像上，找到 \(x = 20\) 时，对应的 Likelihood.

如果学过概率论，就知道这对应的是正态分布概率密度函数中，这个 \(x\) 值对应的纵轴的值。

我们把这几个指标的 Likelihood 都算出来，然后乘起来，再乘以我们刚刚说的“先验概率”。\(P(L) \times P( \text{Popcorn} = 20 | L) \times P( \text{Soda} = 500 | L) \times P( \text{Candy} = 25 | L)\)。这个值的结果，就是我们判断的，这个人喜欢Troll2这个电影的概率。

注意：这里有一个点。在正态分布图上求 Likelihood，很可能会算出某个likelihood特别小。在计算时出现 Underflow 的现象。比如，可能一个是 0.05，一个是0.0004，一个是0.006，相乘，数字会非常小。

因此，很多时候我们会对算出来的值取 Log (一般用 e 为底的对数)。 此时，我们也就把中间的乘法变成加法了。

我们计算出，在 \(L\) 的情况下，结果是 -124。

同理，我们也可以算出，在 \(N\) 的情况下的结果，假设结果是 -48.

第三件事

好了！我们发现，-48 > -124。所以，我们应该认为，这个人属于"N"类。

一个扩展

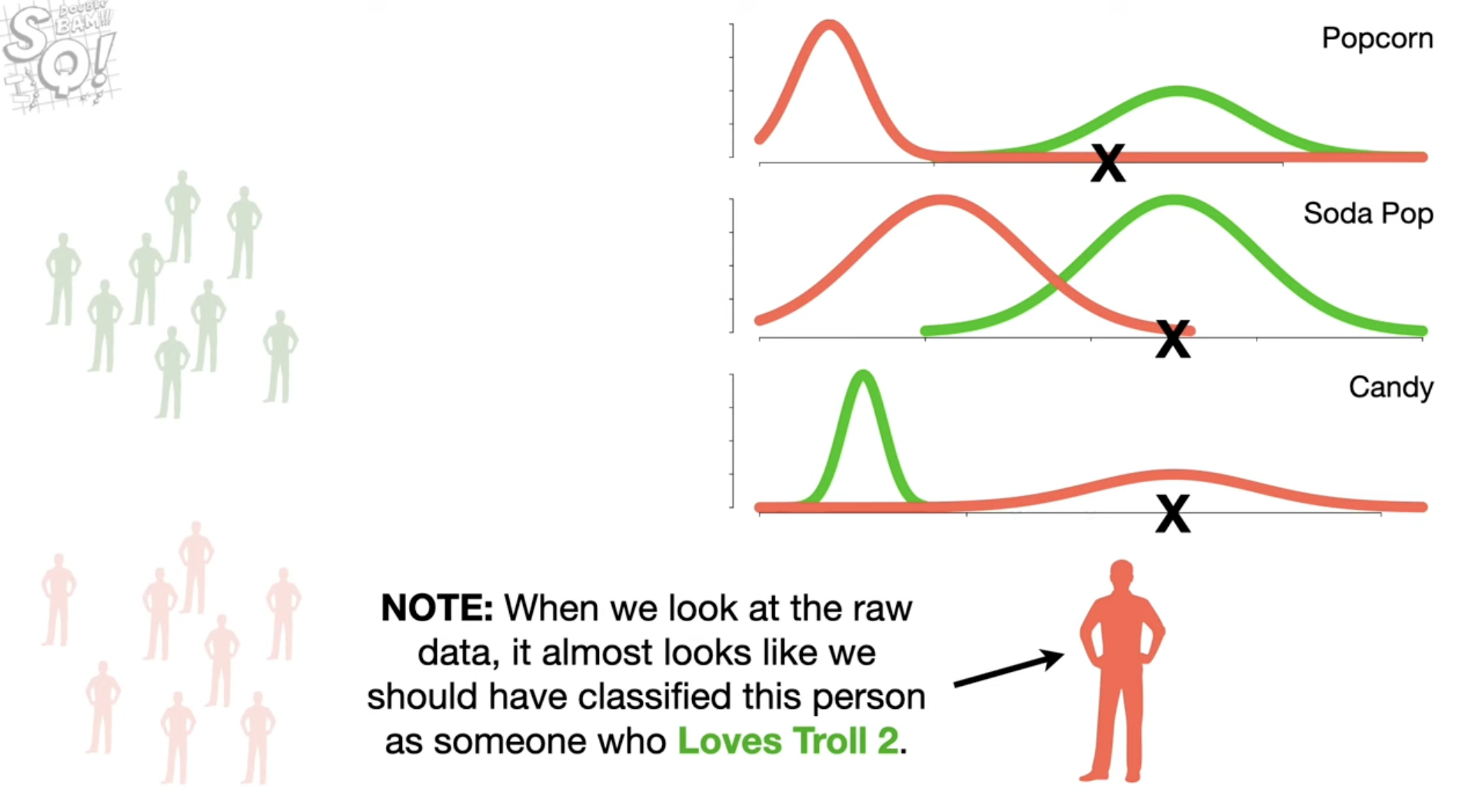
我们用红色表示“N”的人的指标的高斯分布，用绿色表示“Y”的人的指标的高斯分布。用X表示测试的这个新样本的指标。会发现，如果只看前两个指标，这个人似乎更应被分到绿色的，也就是“Y”这一类中。毕竟它的这两个指标更接近绿色的分布，并且距离红色分布都有相当的距离。

但是，为什么高斯朴素贝叶斯会分到“N”中呢？

重点就在第三个特征。这个人的Candy摄入，远远大于那些“Y”的人的摄入（绿线），这也就导致了在Candy这个指标下算出的Likelihood的Log值，差距很大，大到远超前两个指标对分类的影响。

🤔 这就足以让人思考了。我们可以用什么方法判断出，这三个指标，Popcorn，Soda和Candy，哪个更能帮我们做出更好的决策。

这就需要介绍：交叉验证（Cross Validation）。