Page Rank Algorithm

约 1117 个字 27 行代码 1 张图片 预计阅读时间 4 分钟

PageRank 是一种用于评估有向图中节点重要性的方法。也就是说，根据一个网络中边的连接关系，给出每一个节点的重要性得分。

常用于网页排序，社交分析 等。比如搜索引擎。

算法思想

PageRank的核心思想是假设==如果一个网页被许多其他重要的网页链接，那么该网页也被视为重要的==。换句话说，PageRank通过分析网页之间的相互链接关系，判断每个网页的权重。

算法流程：

初始化：

为网络中的每个网页分配一个初始的PageRank值，通常设为相等。

迭代计算：

对于每个网页，计算其新的PageRank值，该值由所有链接到该网页的其他网页的PageRank值贡献。具体而言，一个网页的PageRank值被均等地分配给它链接到的所有网页。

引入阻尼因子（damping factor）：

为模拟用户在浏览网页时可能随机跳转到其他页面的行为，引入阻尼因子 \(d\)（通常设为\(0.85\)）。这意味着用户有\(85\%\)的概率通过链接继续浏览，有\(15\%\)的概率随机跳转到其他页面。

重复迭代：

不断重复上述计算过程，直到PageRank值收敛到一个范围内：相邻两次迭代的值变化在可接受范围内。

我们用 \(R_i\) 表示一个向量，表示第 \(i\) 次迭代时节点的权重，每一个元素代表一个节点的权重；用 \(M\) 表示转移矩阵。\(d\) 表示阻尼因子。因此我们得到了迭代方程：

\[R_{i+1} = d \cdot M R_i + \frac{1-d}{n} \cdot \textbf{1}\]

第一个问题就是，\(M\) 矩阵是如何计算的。

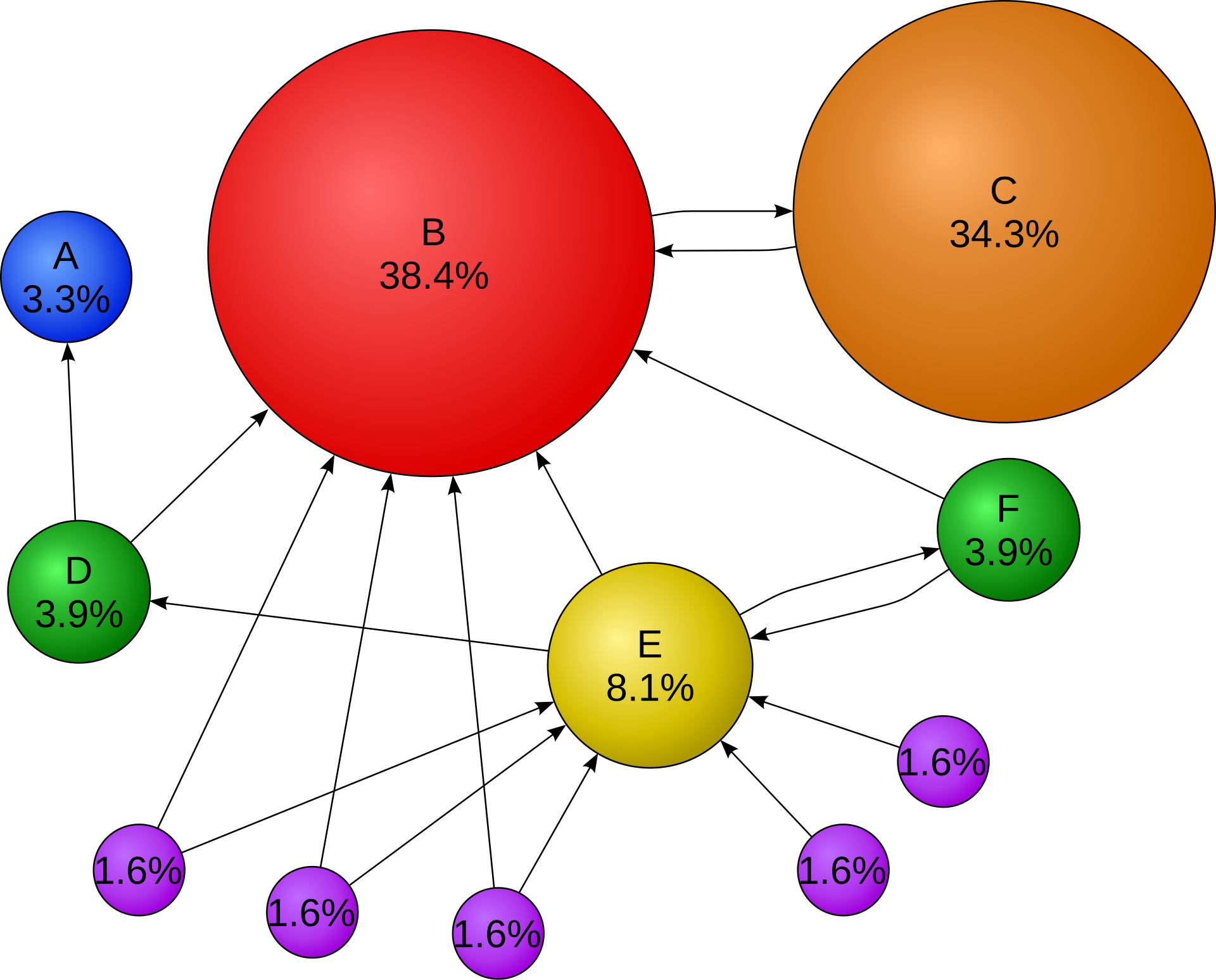
我们考虑这样一张图，用如下矩阵 \(A\) 表示每个节点之间的相连关系，也就是 \(x_{ij} = 1\) 表示有一条边从 \(i\) 流向 \(j\).

\[A = \begin{bmatrix} 
0 & 1 & 1 & 0 & 0 & 1  \\
1 & 0 & 1 & 1 & 0 & 1  \\
0 & 0 & 0 & 0 & 0 & 1  \\
1 & 1 & 0 & 0 & 0 & 1  \\
0 & 0 & 1 & 1 & 0 & 1  \\
1 & 1 & 1 & 0 & 0 & 0  
 \end{bmatrix}\]

行 \(i\) 的和表示节点 \(i\) 的出度。列 \(j\) 的和表示节点 \(j\) 的入度（有多少边指向它）。我们的 \(M\) 矩阵与 \(A\) 矩阵的大小是相同的。对于原先就不存在的边，\(M\) 中对应位置也是0，但是我们要把 \(A\) 中的 1 替换成这个边的权重。我们按照如下规则计算：

对于每一个节点，如果流出它的边数为 \(k\)，那么流入它的每一个边的权重就是 \(1 / k\)。

以节点 \(0\) 为例，看第一行：流出它的共有3条: \((0,1), (0,2), (0,5)\)，那么流入节点 \(0\) 的所有边的权重都为 1/3。所以，我们 \(M\) 矩阵的第一列就是：

\[\begin{bmatrix} 0 \\ 1/3 \\ 0 \\ 1/3 \\ 0 \\ 1/3 \end{bmatrix}\]

同理，对于节点 \(1\)，看第二行：流出它的共有4条: \((1,0), (1,2), (1,3), (1,5)\)，那么流入节点 \(1\) 的所有边的权重都为 1/4。所以，我们 \(M\) 矩阵的第二列：

\[\begin{bmatrix} 0.25 \\ 0 \\ 0 \\ 0.25 \\ 0 \\ 0.25 \end{bmatrix}\]

以及最终的 \(M\) 矩阵：

\[\begin{bmatrix} 
 0         & 1/4 &       1 &          0 &         0 &           1/3 \\
 1/3 & 0 &         1 &           1/3 & 0 &           1/3 \\
 0         & 0 &         0 &          0 &         0 &           1/3 \\
  1/3 & 1/4 &       0 &          0 &         0 &           1/3 \\
 0         & 0 &         1 &           1/3 & 0 &           1/3 \\
  1/3 & 1/4 &       1 &          0 &         0 &          0         \\
 \end{bmatrix}\]

!!! example "主要核心"

- **随机游走模型：** 利用随机游走的概念，模拟用户在网络中的浏览行为。
- **阻尼因子：** 引入阻尼因子，考虑用户随机跳转的可能性，使模型更贴近实际情况。

> 阻尼因子也是为了避免悬挂节点（没有出度的节点）、非强连通图（存在无法相互访问的节点群）等特殊情况

为什么这种方式是靠谱的

这需要我们引入：稳态概率分布：马尔可夫链的收敛性。也就是说，假如一个用户在图中无限次随机跳转（点击链接），最终停留在每个节点的概率会趋于稳定，称为平稳分布。

（感谢Deepseek提供的这个比喻）我们将网页视为房间，链接视为房间之间的门。如果每个房间的人数比例（R）满足“每扇门进出的人数相等”，则总人数比例不再变化。这时 MR=R 就是这种平衡状态的数学表达。

# 调包版
import networkx as nx 
import numpy as np
barabasi_graph = nx.barabasi_albert_graph(60,41) 
matrix = nx.to_numpy_array(barabasi_graph, dtype = np.int16)
pr = nx.pagerank(barabasi_graph,0.85) 
print(np.array( [v for k, v in pr.items()])[:10])
# 调包看看真实的结果

# NumPy手搓版
import numpy as np
def page_rank(matrix, d=0.85, tol=1e-6, max_iter=10000):
    # Page Rank in NumPy!
    out_degree = matrix.sum(axis=1) # 计算每个节点的出度
    weight = matrix / out_degree
    N = matrix.shape[0] 
    pr = np.ones(N).reshape(N, ) * 1.0 / N # 按照出度为每个边赋予权重
    for iter in range(max_iter):
        old_pr = pr.copy()
        pr = d * weight.dot(pr) + (1 - d)/ N # 迭代公式
        err = np.absolute(pr - old_pr).sum() # 满足误差，或者到达最大迭代次数
        if err < tol:
            return pr.T
    return pr.T

if __name__ == "__main__":
    res = page_rank(matrix)
    print(res[:10])