线性回归⚓︎
约 2087 个字 1 张图片 预计阅读时间 7 分钟 总阅读量 次
Main Ideas
- 用最小二乘法来拟合一些数据点;
- 计算 \(R^2\)
- 为计算得到的 \(R^2\) 给出 \(p-value\)
前置概念
- Residuals, Variance
- 本文中会用
SS作为 "Sum of Squares" 的简写。这个操作就是,针对给定数据,计算每个值与这些数均值的差的平方,并求和。 通过这个计算,我们能够知道这组数据的变异程度(离散程度)。比如,对这组数据进行 SS 操作: [1,4, 6, 9]. 我们有: \((1 - 5)^2 + (4 - 5)^2 + (6 - 5)^2 + (9 - 5)^2 = 33\).
\(R^2\) 的解释⚓︎
一言以蔽之,就是我们感兴趣的那个变量 \(Y\) 能够被我们的变量 \(X\) 解释的部分。(fraction of variation explained in Y by X)
- \(SS(Y) = \sum (y_i - \bar{y})^2\) ,total variation in Y
- \(SS(\text{fit}) = \sum (\hat{y_i} - \bar{y})^2\) variation in Y explained by X
引出第一个公式:\(R^2 = \dfrac{SS(Y) - SS(\text{fit})}{SS(Y) }\)。
- \(R^2 = 0\),意味着无法用\(X\)来解释\(Y\);(对应到二维散点图的上,一些点,一条和X轴平行的直线)
- \(R^2 = 1\),意味着所有的 \(Y\)(的误差)都可以被用 \(X\) 解释;
- \(R^2 = 0.8\),意味着80%的\(Y\)的误差可以用\(X\)解释;
所以 \(R^2\) 也被称为
coefficient of determination.
- 皮尔逊相关系数的平方?
- hat 这个符号就用来表示剔除了误差项,仅仅从x回归得到的y的期望值(expected value);
如果是多元线性回归 ..⚓︎
一样的,\(y_i = b_0 + b_1x_1+ b_2x_2 + ... + u_i\)
无论怎么样,\(R^2 = \dfrac{SS(Y) - SS(\text{fit})}{SS(Y) }\) 总是成立的。另一种写法:\(R^2 = \dfrac{\sum (\hat{y_i} - \bar{y})^2}{\sum (y_i - \bar{y})^2}\)
但是需要注意,这也是线性回归到多元线性回归的一个重要变化:
Adding variables will never reduce \(R^2\)
-
如果新增的变量与因变量有一丁点相关性,哪怕这种相关性很弱,是偶然导致的,它也会减少 RSS,使 上升。
-
如果新增的变量与因变量完全(即噪声变量),它对拟合效果并不会有改变,所以最小二乘法会把它的系数置为 0,但 RSS 至少不会变大,因此 \(R^2\) 至少保持不变。
-
那么我们可不可以随意地往这个回归函数里添加变量呢?反正 \(R^2\) 不会变小,随便加呗!
However ...
注意这样一种奇怪的情况。如果一元线性回归的情况下,此时有两个观测,此时的\(R^2 = 1\)(因为这两个点完全解释了这一条直线!但是这并不好!因为它不自由!我们会说,它的自由度是0).
如果有三个观测,自由度是 \(1\),\(R^2\)可能降到\(0.8\),但是此时的模型更好了,因为有了自由度,对模型关系评价的强度就更高了;
但是,如果我总共只有7个数据,我试图用6个自变量来进行线性回归 ... 拟合出来的 \(R^2=1\)!但是此时泛化性并不好。所以:
任意地提高自变量数量,如果不能有目的、有针对地挑选,往往会导致不好的结果。
- 正如上面展开说的那样,其实\(R^2\)本身是很令人疑惑的,因为过高的\(R^2\)可能说明恰恰是缺少了自由度的。
- 比如,对于二元线性回归,我们只有3个点,那么这3个点完全确定了一个面,但是这个面不一定能很好地反映变量间的关系。
此时我们有两个需要:
- 找到一个类似 \(R^2\) 的新的衡量模型的解释能力和复杂度的指标,来反映模型对因变量变异的解释比例。针对这个问题的回答,见下面的 Adjusted \(R^2\)。
- 我们需要一个方法在统计学概率分布的角度判断拟合模型是否是显著的,是否比无自变量的情况更好。也就是需要给出一个 \(p\) 值。针对这个问题的回答,见下面的 \(F\) 检验。
Adjusted \(R^2\)⚓︎
\(\text{Adjusted } R^2 = 1 - \dfrac{[ SS(\text{fit}) ] / (n - p - 1)}{\text{SS}(\text{mean}) / (n - 1)}\)
记录
- 更多自变量,即使这变量与\(Y\)不相关,总有一部分\(Y\)能被\(X\)所解释;\(R^2\) 会变大;
- 在同等多数据的情况下,自变量 (
regressors)越来越多,也意味着自由度越来越低;更低的自由度往往意味着更高的\(R^2\);
我们记修正后的 \(R^2\) 为 \(\bar{R^2}\)。其概念在于,如果加入一个变量,产生的上述如 1 的作用大于 2 的作用,那么 \(\bar{R^2}\) 就会增加,反之减少。这个 \(\bar{R^2}\) 只在“你加入了一些解释变量,而且这些解释变量的解释力度大于自由度减少带来的解释力度,也就是更好滴提升模型预测能力”的时候才增加。
调整后的 \( R^2 \) 在计算时加入了惩罚项,针对模型的变量数量进行调整,从而避免仅靠增加变量就提高 \( R^2 \) 的现象。
使用调整后的 \( R^2 \) 有助于选择既高效又不复杂的模型,尤其是在多元回归分析中。
F 检验⚓︎
\(F =\) 能够被 \(X\) 解释的 \(Y\) 的误差 / 不能被 \(X\) 解释的 \(Y\) 的误差变化。
\[F = \dfrac{ [SS(\text{mean}) - SS(\text{fit}) ] / (p_{\text{fit}} - p_{\text{mean}})}{SS(\text{fit}) / (n - p_{\text{fit}})}\]
这个公式可以告诉我们, \(R^2\) 是否是显著的。
这里,\(p_{\text{fit}}\) 指的是拟合时所用到的参数的数量 (number of parameters in the fit line)。以简单的线性回归为例:\(y = ax + b\),我们的参数有2个 (a, b),那 \(p_{\text{fit}} = 2\)。
这里,\(p_{\text{mean}}\) 指的是计算 mean-line 时候的参数的数量 (number of parameters in the mean line),以简单线性回归为例,我们只有一个 \(y\),所以这里的参数只有一个:\(y\) 的均值。此时,分子上的除数就是 \(2 - 1 = 1\)
注:在许多教材中,这里的 \(p_{\text{fit}} - p_{\text{mean}}\) 一般写作 \(p\),也就是自变量个数。此时\(p_{\text{fit}} - p_{\text{mean}}\)就是 \(n - p - 1\)
拓展一点讲,如果是个多元的线性回归,很明显 \(p_{\text{fit}}\) 就要更多: \(y = ax + bz + c\) ,此时就有 3 个参数咯!
这个分子,实际上就是计算了由所有自变量解释的因变量的变化。
如果我们看分母,这个分母的含义就是因变量中不能被自变量解释的变化 (Variance that can't be explained by the fit)。
为什么分母除以 \(n - p_\text{fit}\)
Intuitively, the more parameters you have in your equation, the more data you need to estimate them. For example, you only need two points to estimate a line, but you need 3 points to estimate a plane.
原因就是上面提到的,随着自变量的增多,我们需要更多的数据来估计这些参数。所以,分母中,\(n - p_\text{fit}\) 就是用来衡量,我们有多少数据来估计这些参数的,也就是,自由的数据的数量。
我们可以画出 \(F\) 分布的图等,以此计算 p-val。某种程度下,可以通过生成很多随机分布数据,计算这个值,绘制分布。然后结合分布,判断我们某个 结果是否是显著的。
p-value is the number of more extreme values devided by all the values.
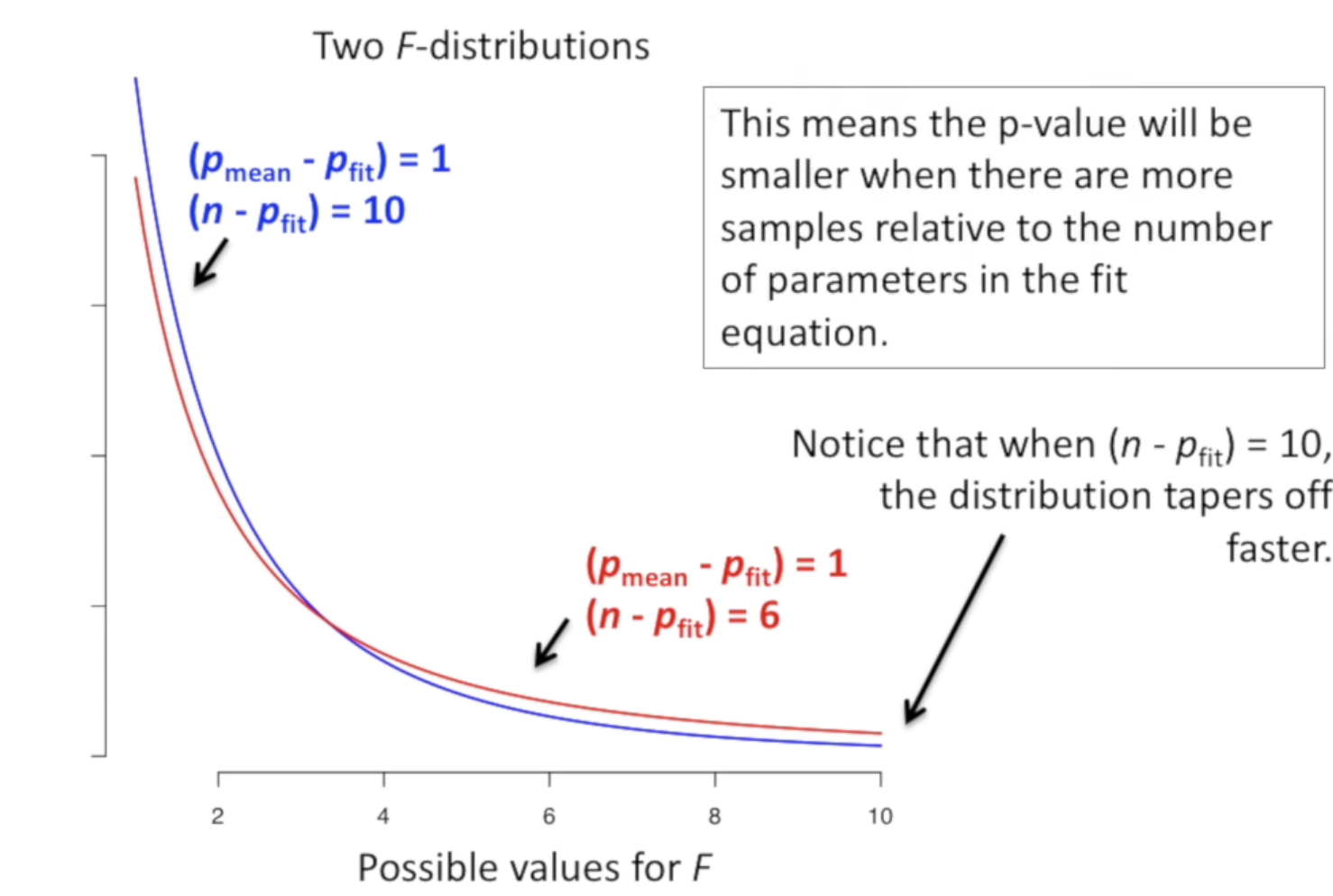
但是。我们还可以更近一步 ...
事实上我们有时候并不知道某个自变量是否有助于解释Y。我们需要事先判断一下是否值得我们搜集这个自变量的数据。我们可以用如下方法计算 F :
我们记不包含某个自变量的回归为Simple,包含后的多元回归为Multiple.
我们就有:
\[F = \dfrac{[\text{SS}(\text{simple}) - \text{SS}(\text{multiple}) ]/ (p_{\text{multiple}} - p_{\text{simple}})}{\text{SS}(\text{multiple}) / (n - p_{\text{multiple}})}\]
可以看到,我们不再用 SS(mean ) 了,而是替换成不包含这个变量的、简单的回归模型时的误差了。
可以想见,如果我们发现,用Simple和Multiple方法进行拟合的时候,\(R^2\) 的差距比较大, 同时,p-value 够小的话,我们就有足够的理由认为,这个变量是值得我们去收集数据的。