从奇异值分解(SVD)到主成分分析(PCA)⚓︎
约 4159 个字 5 张图片 预计阅读时间 14 分钟 总阅读量 次
复习:前置知识⚓︎
正交矩阵 (Orthogonal Matrix)
我们可以从一些标准正交向量开始掌握“正交”。设想一些列向量 \(\mathbf{q_1}, \mathbf{q_2}, ..., \mathbf{q_n}\) 满足:
\[\mathbf{q^T_i q_j} = \begin{aligned}
\begin{cases}
1 \qquad \text{if} \qquad i = j \\
0 \qquad \text{if} \qquad i \neq j
\end{cases}
\end{aligned}\]
那它们就是互相正交的。(由于进行标准化成1了,所以是标准正交的)。
然后,我们把它们以列向量的形式写成一个矩阵:
\(\mathbf{Q} = \begin{bmatrix} \mathbf{q_1} & \mathbf{q_2} & ... & \mathbf{q_n} \end{bmatrix}\)
此时我们计算 \(\mathbf{Q^T Q} = \begin{bmatrix} \mathbf{q^T_1} \\ \mathbf{q^T_2} \\ ... \\ \mathbf{q^T_n} \\ \end{bmatrix} \begin{bmatrix} \mathbf{q_1} & \mathbf{q_2} & ... & \mathbf{q_n} \end{bmatrix}\)
你会得到: \(\mathbf{Q^T Q}= \mathbf{I}\)。
对于由标准正交列向量构成的方阵,我们统称为 正交矩阵。它具有很好的性质: \(\mathbf{Q^T} = \mathbf{Q^{-1}}\)
矩阵的特征值 (Eigenvalues) 和特征向量 (Eigenvectors )
对于一个 \(n \times n\) 的方阵 \(\mathbf{A}\) ,我们希望找到这样的一些向量 \(\mathbf{x}\),使得它与 \(\mathbf{A}\) 相乘之后得到的新向量,依然和它指向同一个方向。也就是:
\[\mathbf{A} \mathbf{x} = \lambda \mathbf{x}\]
这样的向量 \(\mathbf{x}\) 就是特征向量,而对应的 \(\lambda\) 就是特征值。
你同样应该知道如何去计算一个方阵的特征值:比如可以对矩阵进行操作: \((\mathbf{A} - \lambda \mathbf{I}) \mathbf{x} = \mathbf{0}\),进而利用行列式的性质列特征方程:\(\det |\mathbf{A} - \lambda \mathbf{I} | = 0\),进而计算出 \(\lambda\),和特征向量 \(\mathbf{x}\)。
矩阵的对角化 (Diagonalization)
对于一个 \(n \times n\) 的方阵 \(\mathbf{A}\),我们以它的所有特征向量为列,构成一个新矩阵 \(\mathbf{S}\)(注意,我们需要 \(n\) 个线性无关的特征向量,否则无法对角化)。
我们有: \(\mathbf{A} \begin{bmatrix} \mathbf{x_1} & \mathbf{x_2} & ... & \mathbf{x_n} \end{bmatrix} = \begin{bmatrix} \mathbf{x_1} & \mathbf{x_2} & ... & \mathbf{x_n} \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & ... & 0 \\ 0 & \lambda_2 & ... & 0 \\ 0 & ...& ... & 0 \\ 0 & ... & ... & \lambda_n \end{bmatrix} = \mathbf{S} \Lambda\)
而因为我们的特征向量是线性无关的,所以一定可逆,于是上式两边同时左乘 \(\mathbf{S^{-1}}\),有: \(\mathbf{S^{-1}AS} = \Lambda\)。另一种形式,是在上式两遍同时右乘 \(\mathbf{S^{-1}}\),有 \(\mathbf{A} = \mathbf{S^{-1}}\Lambda\mathbf{S}\)。这就是方阵 \(A\) 的另一种分解:方阵的对角化(Diagnoalization)。
一个简单的理解是,将一个方阵分解成了三个矩阵的乘积。
奇异值分解(Singular Value Decomposition)⚓︎
现在我们终于可以进入奇异值分解的内容。SVD 是一种经典的==无监督学习==的算法。
与对角化十分类似,我们也是将一个矩阵进行分解,不同的是,我们可以对任意的 \(m\times n\) 的矩阵 \(\mathbf{A}\) 进行这个操作。我们可以把它分解成如下的形式:
\[\mathbf{A} = \mathbf{U} \Sigma \mathbf{V^T}\]
其中,\(\mathbf{U}\) 是一个正交矩阵,\(\Sigma\) 是一个对角矩阵,而 \(\mathbf{ V^T}\) 也是一个正交矩阵。
如果你熟悉正交矩阵和对角矩阵在空间变换上的作用,你可以发现我们相当于进行了“旋转” 、“拉伸”、“旋转”,三个操作。
与对角化不同的是,我们的 \(\Sigma\) 不再是由特征值组成的,而是 由奇异值组成的对角矩阵 ;我们左右的矩阵,也 不再是由特征向量为列向量组成的矩阵和它的逆,而是两个完全不同的矩阵了 。
你可以看作:
\[\mathbf{A} = \begin{bmatrix} \mathbf{u_1} & \mathbf{u}_2 \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \end{bmatrix} \begin{bmatrix} \mathbf{v_1} \\ \mathbf{v_2} \end{bmatrix}\]
现在我们作一些简单的推导:
\(\mathbf{A} = \mathbf{U} \Sigma \mathbf{V^T}\)
我们用 \(\mathbf{A^T}\) 左乘,得到:
\(\mathbf{A^TA} = \mathbf{V} \Sigma^T \mathbf{U^T} \mathbf{U} \Sigma \mathbf{V^T}\)
考虑到 \(\mathbf{U}\) 是正交的,消去可得:
\(\mathbf{A^TA} = \mathbf{V} (\Sigma^T \Sigma) \mathbf{V^T}\)
注意到 \(\Sigma^T \Sigma\) 的结果是一个对角矩阵,同时我们用 \(\mathbf{A^T A}\) 得到了一个半正定矩阵,也是对称的。
这同样说明了,
- \(\mathbf{A^T A}\) 的特征值,就是 \(\mathbf{A}\) 的奇异值的平方。
- \(\mathbf{V}\) 对应了 \(\mathbf{A^TA}\) 的特征矩阵 。为什么呢?因为 \(\mathbf{V}\) 是正交矩阵,所以 \(\mathbf{V^T} = \mathbf{V^{-1}}\),也就是 \(\mathbf{A^TA} = \mathbf{V} (\Sigma^T \Sigma) \mathbf{V^{-1}}\),正好与前面根据特征值进行矩阵对角化的式子是一样的。
那么如何获得 \(\mathbf{U}\)?只需要用同样方法,计算 \(\mathbf{AA^T} = \mathbf{U} \Sigma \mathbf{V^T} \mathbf{V} \Sigma^T \mathbf{U^T} = \mathbf{U} \Sigma \Sigma^T \mathbf{U^T}\),由于 \(\mathbf{A A^T}\) 和 \(\mathbf{A^T A}\) 有一样的特征值,根据前面的推导,我们有:
- \(\mathbf{U}\) 对应了 \(\mathbf{AA^T}\) 的特征矩阵 。
换句话说,SVD之所以对所有 \(m \times n\) 的矩阵 \(\mathbf{A}\) 都可以操作,就是因为,不管 \(\mathbf{A}\) 的性质如何,我只要:
- 找到 \(\mathbf{A^TA}\) 的特征矩阵,以及 \(\mathbf{A A^T}\) 的特征矩阵(P.S. 矩阵和它转置乘下来一定是一个方阵,所以一定可以找特征值),
- 把这两个特征矩阵,与 \(\mathbf{A}\) 的奇异值(恰好也可以通过 \(\mathbf{A^T A}\) 的特征值求到)构成的对角矩阵拼起来,得到 \(\mathbf{A}\) 了。
主成分分析(PCA)⚓︎
现在,很适合我们引入“主成分分析”相关的内容。我们先考虑这样一个场景:
在生命科学领域,我们测试不同人的基因表达数据,把它存在矩阵里,比如一个矩阵,一列表示一个人的基因数据,每一行表示每个基因的表示情况。每个元素就表示,每个人表示了多少这个基因。
现在我们可能想从这些数据里获得一些“基因-人”之间的洞察。比如有某种疾病的人的某些基因之间的联系:患某种病的人有些共性的“基因组合(A mixture of Gene)”,它们对结果的影响最大。 注意,我们并不会选某个人的某些基因,而是要找样本集合中最有代表性的那些基因组合。
此时我们就需要充分利用 SVD。注意到,如果我们把找到的奇异值按照从大到小排序, 那么, \(\Sigma\) 的第一个奇异值,就是我们想要的,而它又对应着, \(\mathbf{U}\) 矩阵的第一列,以及 \(\mathbf{V^T}\) 的第一行(即 \(\mathbf{u_1}, \mathbf{v^T_1}, \sigma_1\)),它们 才是我最感兴趣的那个特征 。在统计学上称:它的方差最好,也就是最富有信息的。
如果我们不只想知道一个特征,我们想知道 \(k\) 个有代表性的特征,那也很简单,你只需要取从大到小排序之后前 \(k\) 个奇异值,就可以了。
而它们意味着什么?以基因-人的例子来说,\(\mathbf{u_1}\) 代表了人的某种组合,而 \(\mathbf{v^T_1}\) 代表了基因的某种组合,而 \(\sigma_1\) 则代表了它们能达到的最大值。
可视化地理解一下⚓︎
现在我们从可视化的角度看看基于这个场景我们是怎么做PCA的。
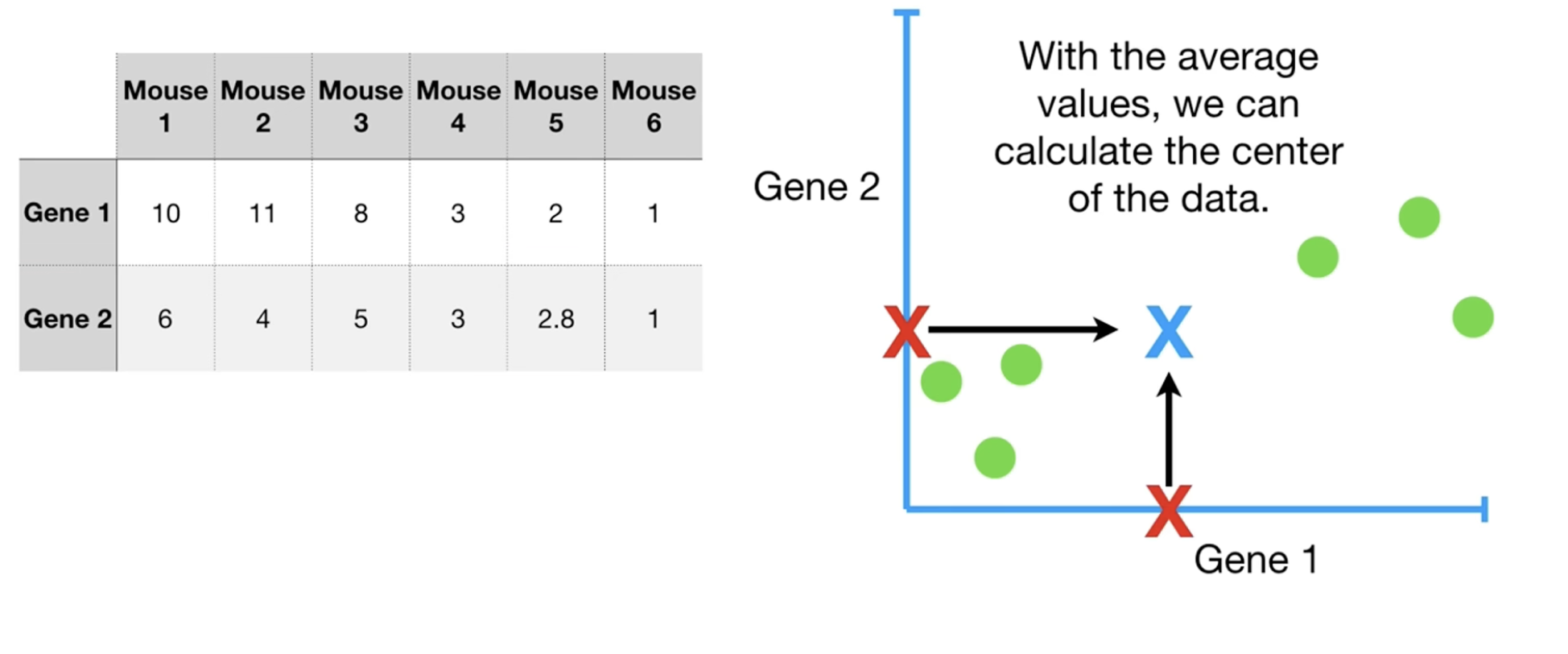
我们以2维数据为例,首先画出散点图,然后稍微做一些处理:按照中心把这些偏离原点的散点以成以原点为中心。
然后我们要做的事和线性回归、最小二乘非常相似:找一条直线,能够最好地拟合这些散点,同时直线经过原点。
如何判断直线的拟合程度?
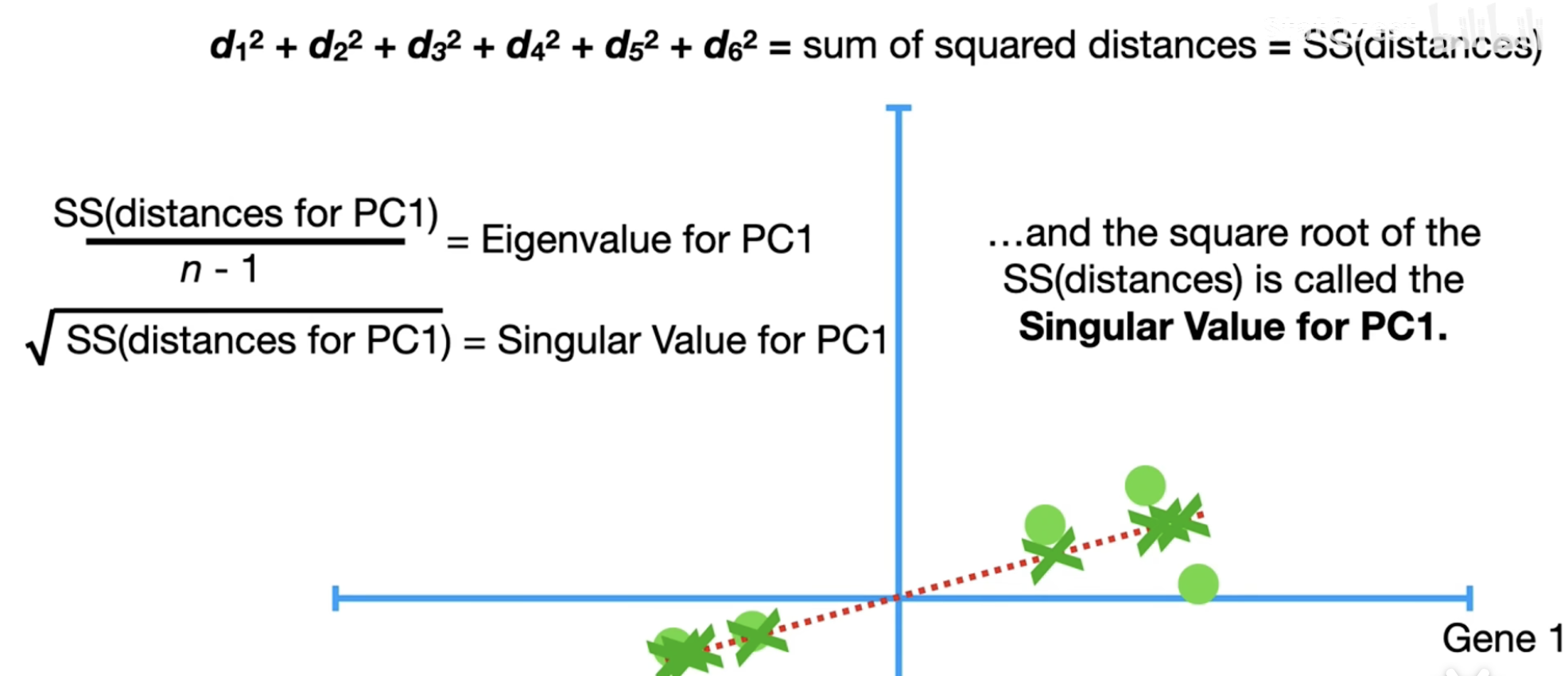
在这个例子里,我们随便画一条线,对每个样本点,作这个直线的垂线,于是每个样本点对应一个投影点。 我们想最大化所有样本投影点到原点的距离的平方和 。事实上,这等价于“最小化所有样本点的投影距离”(你可以借助勾股定理)。但是在这个场景下,我们认为第一种方法更好懂一点,我们上文提到的“方差最大”,你可以理解为平方和再除以 \(n - 1\),即 \(\dfrac{\text{sum of squared distance}}{n - 1}\)。 反映的就是,这一条线它覆盖的样本点的范围。我们当然希望它尽可能地大了,这样才表明我们这一条线更好地覆盖了尽可能多的某种特征。
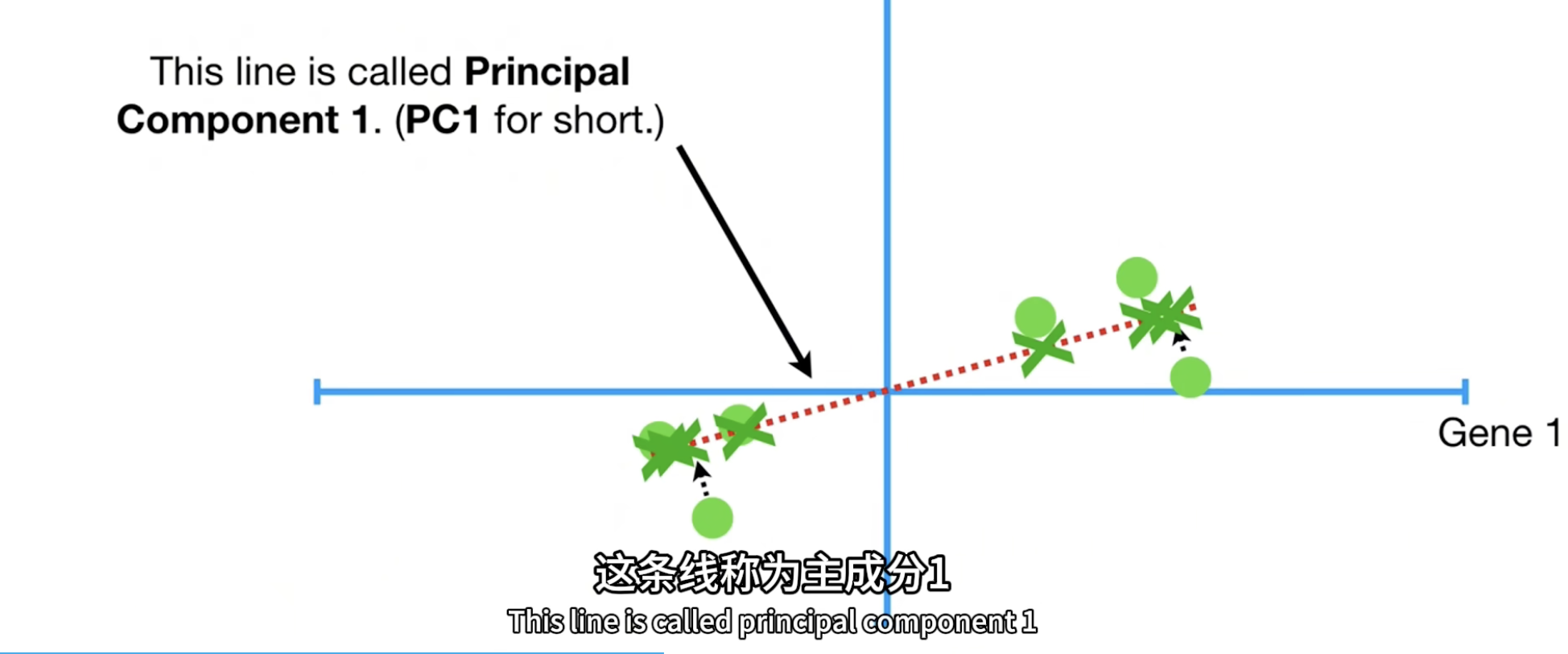
我们画出一条线后,命名为 PC-1。它代表了某种基因的组合,比如假如它方向是 \((4, 1)\),的斜率是 0.25,意味着它在 Gene 1 上走了4个单位,才在 Gene 2 上走了 1个单位。也可以说,它对 Gene 1 是比较分散的(方差很大),但是 Gene 2 是比较集中的。不过一般而言我们会在这里把这个向量标准化为 1,也就是 \((0.97, 0.24)\)。
这个向量,就对应着我们 \(\mathbf{V}\) 矩阵的一个特征向量。而==刚刚计算的那个方差,就对应了这个PC-1的特征值,其实也就是SVD中, \(\mathbf{A^TA}\) 方阵里最大的那个特征值==。
从 SVD 的计算我们知道,我们把这个特征值开根号,也就得到了我们最大的那个奇异值。
第二个主成分怎么找呢?毫无疑问我们需要找的是一条和 PC-1正交(垂直)的线(下图蓝线),毕竟SVD里面,我们的 \(\mathbf{U}, \mathbf{V}\) 都是正交矩阵。我们命名这个线为 PC-2
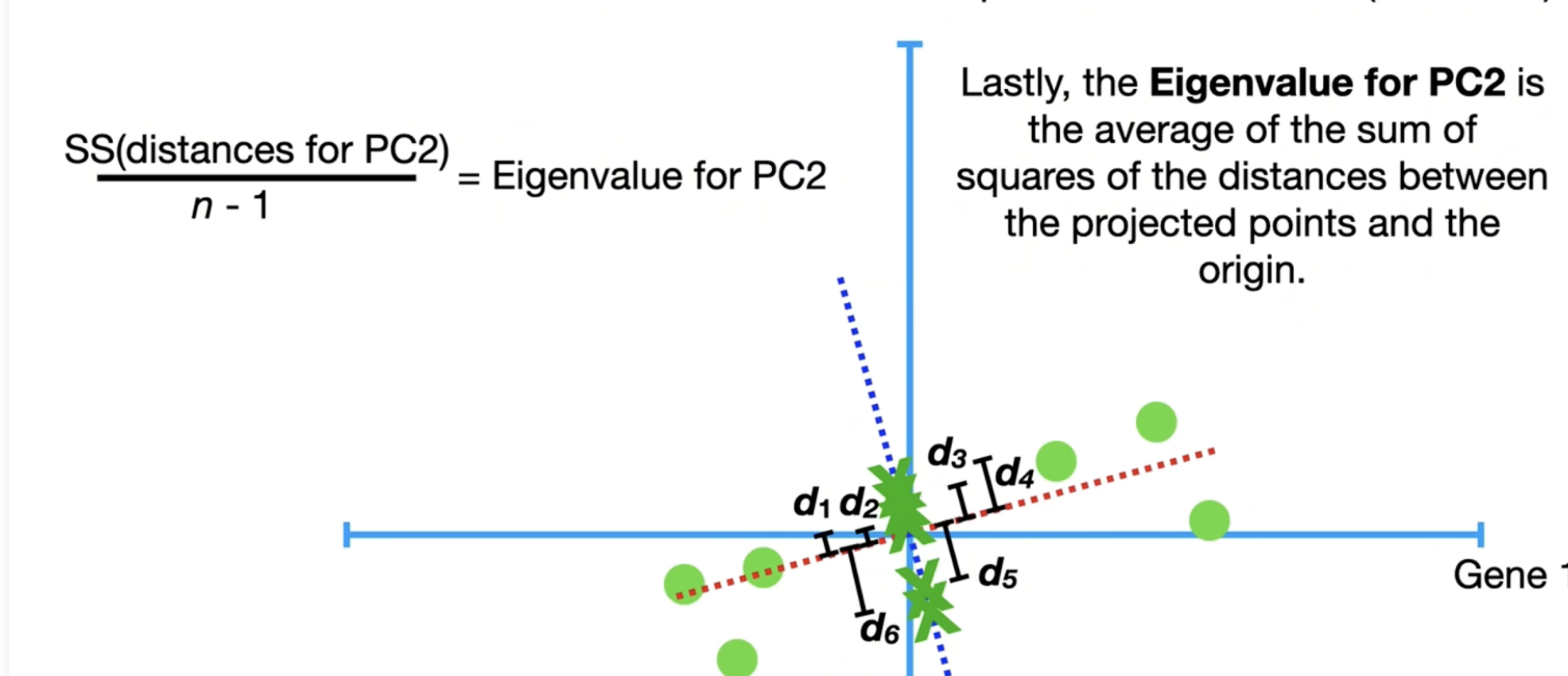
现在我们甚至可以画出PCA之后,原先样本点的情况:只需要把正交的PC-1,PC-2画成坐标系,然后把对应投影点画出来反推出样品点,就可以了。
此时,我们同样能回答,在高于二维的更高维度下,“下一个主成分怎么找”这个问题:不断地找先前已有的所有主成分的另一些正交向量。
我们同样可以发现,对于每一个主成分,我们都算了一次方差。事实上,我们可以通过这个成分的方差占所有成分的方差和的百分比,来评估这种“主成分”的重要性。 我们也就可以筛选出,要想能够解释 \(x \%\)方差的话,需要哪些主成分。
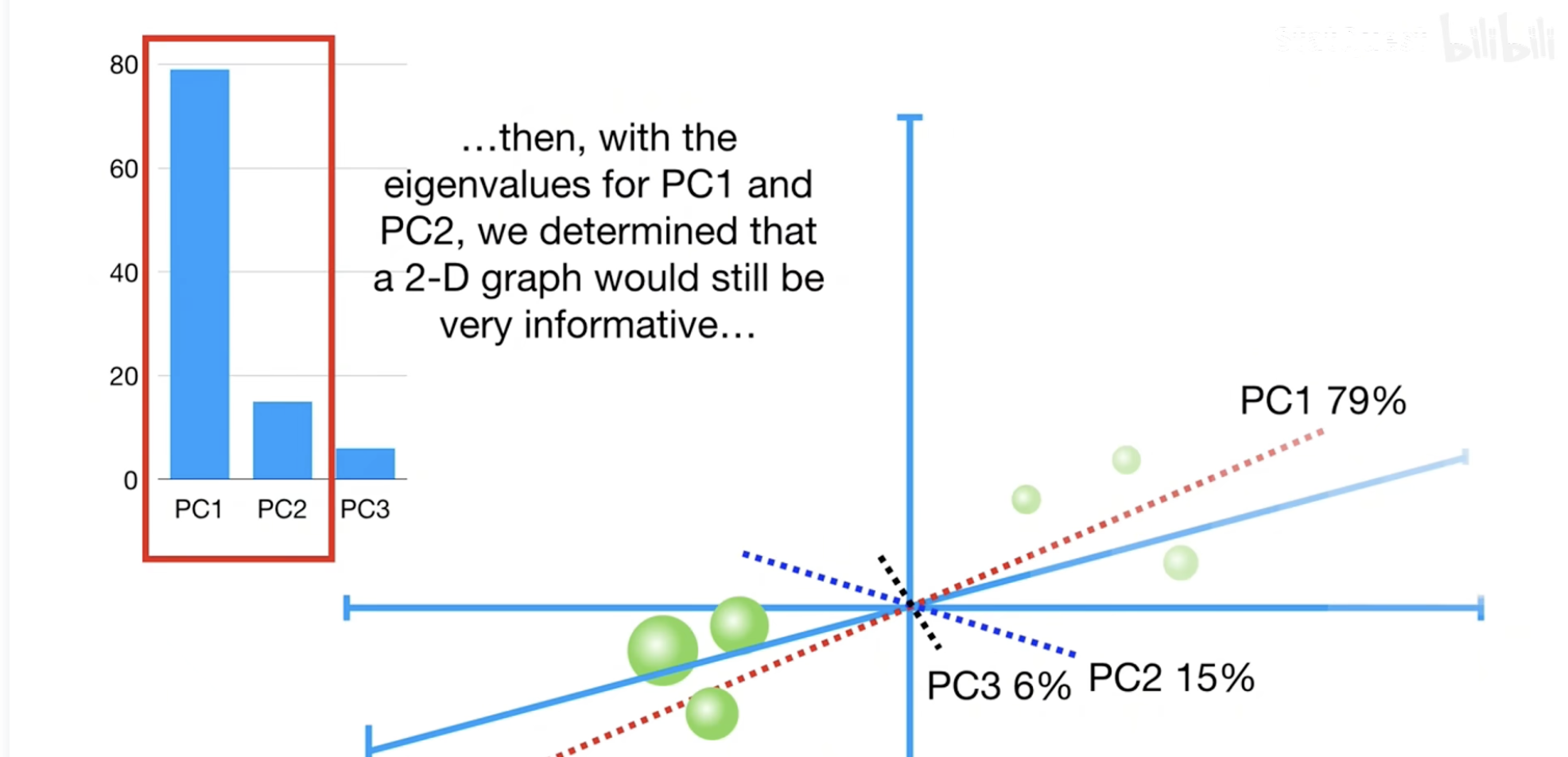
除了识别主成分外,还有一个潜在的作用。如果某个PCA发现,前4个主成分对方差的占比差别不大,我们也可以识别出可能存在一些数据的聚类。
PCA的算法复杂度分析⚓︎
假设我们有 \(n\) 个样本和 \(m\) 个特征,数据矩阵 \(\mathbf{X}\) 的维度是 \(n \times m\)。
设定:我们的数据矩阵为 \(\mathbf{X}\),维度为 \(n \times m\)(\(n\) 个样本, \(m\) 个特征)。我们希望将其降到 \(k\) 维。
整个过程可以分为三步: 1. 数据中心化 2. 对中心化后的矩阵进行SVD分解 3. 得到降维后的数据
下面我们对每一步涉及的矩阵运算及其复杂度进行详细分析。
第 1 步:数据中心化⚓︎
目标:得到中心化矩阵 \(\mathbf{X}_{centered}\),使得其每个特征(列)的均值为0。
矩阵运算: 1. 计算均值向量: 计算 \(\mathbf{X}\) 每一列的均值。 - 运算: 对一个 \(n \times 1\) 的列向量求和(\(n-1\) 次加法)然后除以 \(n\)。 - 维度: 我们需要对 \(m\) 列都进行这个操作。 - 复杂度: \(O(n)\) 的操作执行 \(m\) 次,所以这一步的复杂度是 \(\mathbf{O(nm)}\)。 2. 广播和减法: 从 \(\mathbf{X}\) 的每一列中减去对应的均值。 - 运算: 这是一个 \(n \times m\) 矩阵减去一个 \(1 \times m\) 的均值向量(该向量会被“广播”成 \(n \times m\))。 - 维度: 这需要 \(n \times m\) 次减法操作。 - 复杂度: \(\mathbf{O(nm)}\)。
该步总复杂度: \(O(nm) + O(nm) = \mathbf{O(nm)}\)。 这是一个线性时间复杂度的预处理步骤,通常不是整个算法的瓶颈。
第 2 步:SVD分解 (核心步骤)⚓︎
目标:对 \(n \times m\) 的中心化矩阵 \(\mathbf{X}_{centered}\) 进行奇异值分解,得到 \(\mathbf{X}_{centered} = \mathbf{U} \Sigma \mathbf{V^T}\)。
这是整个PCA算法中计算量最大的部分。现代数值计算库中SVD的实现非常复杂,但其复杂度可以从其背后的数学原理来理解。SVD的算法复杂度取决于矩阵的维度 \(n\) 和 \(m\)。
核心思想:SVD的计算与两个关键的对称矩阵的特征值分解紧密相关: * \(\mathbf{X}_{centered}^T \mathbf{X}_{centered}\) (一个 \(m \times m\) 的矩阵, 与协方差矩阵成正比) * \(\mathbf{X}_{centered} \mathbf{X}_{centered}^T\) (一个 \(n \times n\) 的矩阵, 称为格拉姆矩阵)
SVD的数值算法会隐式地选择计算代价更小的方式进行。
-
如果 \(n \ge m\) (样本数多于特征数):算法倾向于基于 \(m \times m\) 的协方差矩阵进行。
- 形成 \(\mathbf{X}_{centered}^T \mathbf{X}_{centered}\):
- 运算: 一个 \((m \times n)\) 矩阵乘以一个 \((n \times m)\) 矩阵。
- 复杂度: \(\mathbf{O(nm^2)}\)。
- 对 \(m \times m\) 的方阵进行特征值分解:
- 运算: 求解特征值和特征向量(得到 \(\mathbf{V}\) 和 \(\Sigma^2\))。
- 复杂度: \(\mathbf{O(m^3)}\)。
- 计算 \(\mathbf{U}\): \(\mathbf{U}\) 可以通过 \(\mathbf{U} = \mathbf{X}_{centered} \mathbf{V} \Sigma^{-1}\) 推导出来。
- 运算: \((n \times m)\) 矩阵乘以 \((m \times m)\) 矩阵。
- 复杂度: \(\mathbf{O(nm^2)}\)。
- 总和: 在 \(n \ge m\) 的情况下,总的瓶颈是 \(O(nm^2) + O(m^3)\)。 由于 \(n \ge m\),所以 \(nm^2\) 成为主导项(或者与 \(m^3\) 同阶),总复杂度近似为 \(\mathbf{O(nm^2)}\)。
- 形成 \(\mathbf{X}_{centered}^T \mathbf{X}_{centered}\):
-
如果 \(m > n\) (特征数多于样本数):算法会巧妙地选择基于更小的 \(n \times n\) 格拉姆矩阵进行。
- 形成 \(\mathbf{X}_{centered} \mathbf{X}_{centered}^T\):
- 运算: 一个 \((n \times m)\) 矩阵乘以一个 \((m \times n)\) 矩阵。
- 复杂度: \(\mathbf{O(n^2m)}\)。
- 对 \(n \times n\) 的方阵进行特征值分解:
- 运算: 求解特征值和特征向量(得到 \(\mathbf{U}\) 和 \(\Sigma^2\))。
- 复杂度: \(\mathbf{O(n^3)}\)。
- 计算 \(\mathbf{V}\): 可以通过 \(\mathbf{V}=\mathbf{X}_{centered}^T\mathbf{U}\Sigma^{-1}\) 推导。
- 运算: \((m \times n)\) 矩阵乘以 \((n \times n)\) 矩阵。
- 复杂度: \(\mathbf{O(mn^2)}\)。
- 总和: 在 \(m > n\) 的情况下,瓶颈是 \(O(n^2m) + O(n^3)\)。由于 \(m > n\),\(n^2m\) 成为主导项 ,总复杂度近似为 \(\mathbf{O(n^2m)}\)。
- 形成 \(\mathbf{X}_{centered} \mathbf{X}_{centered}^T\):
该步总复杂度: 结合两种情况,在渐进意义下,SVD分解的复杂度是 \(\mathbf{ \min \{O(nm^2), O(mn^2) \}}\)。
当然,如果严谨地说,即 \(n > m\) 的场景下,复杂度一般详细地写作: \(\mathbf{O(nm^2) + O(m^3)}\)
第 3 步:得到降维后的数据⚓︎
目标:得到降维后的 \(n \times k\) 矩阵 \(\mathbf{Z}\)。
矩阵运算: 在SVD方法中,我们有一个非常高效的捷径。降维后的数据(主成分得分)可以直接由 \(\mathbf{U}\) 和 \(\Sigma\) 计算得到:
\[\mathbf{Z} = \mathbf{U}_k \Sigma_k\]
其中 \(\mathbf{U}_k\) 是 \(\mathbf{U}\) 的前 \(k\) 列,\(\Sigma_k\) 是 \(\Sigma\) 左上角的 \(k \times k\) 对角矩阵。
- 运算: 一个 \(n \times k\) 的矩阵 \(\mathbf{U}_k\) 与一个 \(k \times k\) 的对角矩阵 \(\Sigma_k\) 相乘。这等价于将 \(\mathbf{U}_k\) 的每一列分别乘以 \(\Sigma_k\) 的对角线元素(即奇异值 \(\sigma_1, \sigma_2, ..., \sigma_k\))。
- 维度: 这需要 \(n \times k\) 次乘法操作。
- 复杂度: \(\mathbf{O(nk)}\)。
注意: 如果不走这个捷径,而是按照传统的投影方式 \(\mathbf{Z} = \mathbf{X}_{centered} \mathbf{V}_k\) 计算,其中 \(\mathbf{V}_k\) 是 \(\mathbf{V}\) 的前 \(k\) 列,则复杂度会是 \(O(nmk)\)。但既然我们已经费力得到了 \(\mathbf{U}\) 和 \(\Sigma\),直接使用它们是更明智和高效的选择。
总结与最终复杂度⚓︎
我们将每一步的复杂度汇总一下:
| 步骤 | 操作 | 输入/输出维度 | 复杂度 |
|---|---|---|---|
| 步骤 1 | 数据中心化 | In: \(n \times m\) Out: \(n \times m\) |
\(O(nm)\) |
| 步骤 2 | SVD分解 | In: \(n \times m\) Out: \(U(n \times n)\), \(\Sigma(n \times m)\), \(V(m \times m)\) |
\(O(\min(n^2m, nm^2))\) |
| 步骤 3 | 计算降维数据 | In: \(U(n \times k)\), \(\Sigma(k \times k)\) Out: \(n \times k\) |
\(O(nk)\) |
总复杂度:
\[O(nm) + O(\min(n^2m, nm^2)) + O(nk)\]
在典型的机器学习场景中,\(k\)(目标维度)远小于 \(n\) 和 \(m\)。因此,SVD分解步骤的计算量是压倒性的瓶颈。
所以,我们可以认为 PCA的整体算法复杂度由SVD决定,为: \(\mathbf{O(\min(n^2m, nm^2))}\),在广泛的 \(n > m\) 的情况下,详细地公式写作:
\(\mathbf{O( nm^2 + m^3)}\)