Transformer⚓︎

约 23660 个字 130 行代码 2 张图片预计阅读时间 80 分钟总阅读量次

神经网络，不会在代码中明确定义如何执行一个任务，而是去构建一个具有可调参数的灵活架构，就像旋钮一样，然后用大量实例告诉它给定一个输入的时候应该输出什么，设法调整各种参数值来模拟这种行为。

但是并不只是直接扩大参数量，而是说需要用灵活的方法进行训练：反向传播（Back- propagation）

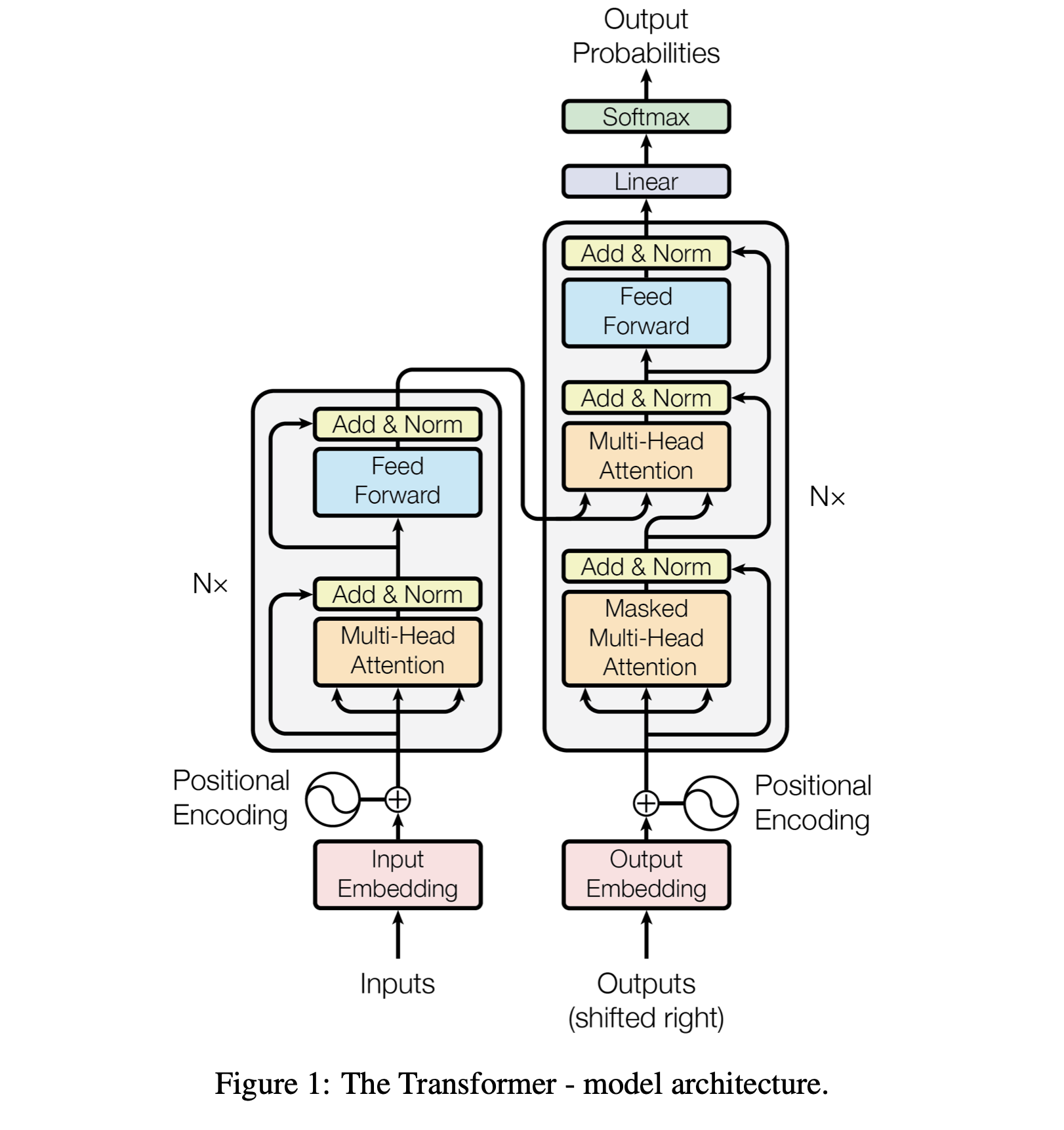
为了这种训练算法的有效运行，模型必须遵循某种特定结构。Attention is all you need.

什么是 KV-cache？

它是什么：KV Cache 是一种针对 Transformer 模型在自回归推理（如文本生成）时的关键优化技术。

目的：解决在生成每一个新 token 时，对历史序列进行大量重复计算的问题，从而大幅提升推理速度。

工作原理：它通过缓存（存储）已经计算过的所有 token 的“键（Key）”和“值（Value）”向量。在生成下一个 token 时，模型只需要为当前这一个新 token 计算 Q, K, V，然后从缓存中读取历史 K, V，拼接后进行注意力计算。

这就是自注意力机制（Self-Attention）的核心。在自回归生成第 $t$ 个 token 时，这个新 token 的 Query 向量（$Q_t$）必须与从第 1 个到第 $t$ 个所有 token 的 Key 向量（$K_1, K_2, ..., K_t$）进行点积，来计算注意力权重。这就是“看到前面的所有上下文”的数学体现。

效果与权衡：

巨大收益：将生成长序列的计算复杂度从近似三次⽅降为二次方，极大地加快了生成速度，使大模型能够进行流畅的对话和长文生成。主要代价：占用大量的显存来存储这些 K, V 向量。因此，在实际应用中，模型的最大上下文长度往往受限于 KV Cache 所占用的显存大小。

GQA, MQA 分组多头注意力机制。

生成式大模型的推理

这是一个非常好的问题，它触及了不同 Transformer 架构在推理时的核心差异。你的问题直接关联到模型的两大类别：Encoder-Only 和 Encoder-Decoder。

答案是：这取决于你谈论的是哪种类型的 Transformer 模型。

我们来分别讨论这两种主流架构：

1. Decoder-Only 架构（例如：GPT系列、Llama系列、BLOOM）

这是目前大语言模型（LLM）最主流的架构，我们刚才讨论的自回归生成、KV Cache 等都主要发生在这种模型上。

推理时用到哪些部分？
- 只用到 Decoder 部分。 顾名思义，这种模型根本没有 Encoder。
会用到交叉注意力吗？
- 不会。 因为交叉注意力（Cross-Attention）的定义是：一个部分的 Query（通常来自 Decoder）关注另一个部分的 Key 和 Value（通常来自 Encoder）。既然没有 Encoder，自然也就不存在交叉注意力。
- 在这种架构里，Decoder 模块中的“交叉注意力”层被一个标准的“自注意力”（Self-Attention）层所替代。所以，一个典型的 Decoder-Only 模型的 Decoder Block 包含两个核心部分：
  1. 带掩码的自注意力 (Masked Self-Attention): 用于处理和生成文本。
  2. 前馈网络 (Feed-Forward Network): 用于信息加工。

小结：对于 GPT 这类 Decoder-Only 模型，推理过程就是我们前面详细描述的自回归生成，它只涉及 Decoder 自身，并且只使用自注意力机制。

1. Encoder-Decoder 架构（例如：原始 Transformer、T5、BART）

这类模型常用于需要“转换”的任务，比如机器翻译（一种语言 -> 另一种语言）、文本摘要（长文章 -> 短摘要）。

推理时用到哪些部分？
- Encoder 和 Decoder 都会用到。
会用到交叉注意力吗？
- 会，而且这是关键步骤！

它的推理过程比 Decoder-Only 模型要复杂一些，分为两个主要阶段：

阶段一：编码输入序列 (Encoder Pass)

输入: 将源序列（Source Sequence），比如要翻译的德语句子 "Ich bin ein Berliner"，完整地输入到 Encoder 中。
计算: Encoder 并行地处理整个德语序列，通过多层的自注意力机制，最终为输入序列的每个 token 生成一个富含上下文信息的表示（representation）。我们称这组最终输出的向量为 memory 或 encoder_hidden_states。
产出: 这一整套 memory 向量。请注意：这个 memory 在整个后续的解码过程中是固定不变的，可以被看作是一个只读的知识库。

阶段二：自回归解码 (Decoder Pass)

现在，Decoder 开始一个词一个词地生成目标序列（比如英语句子）。这个过程和 GPT 的自回归很像，但多了一个关键步骤：

起始: Decoder 从一个特殊的起始符 [BOS] (Begin of Sentence) 开始。
循环生成:
- a. 带掩码的自注意力: Decoder 首先对自己已经生成的部分进行自注意力计算。比如生成到第三个词时，它会回顾 [BOS] 和前两个已生成的词。这一步和 GPT 完全一样。
- b. 交叉注意力 (Cross-Attention): 这是核心区别！ 在上一步自注意力的输出之上，Decoder 会执行一个交叉注意力操作。
  - Query: 来自 Decoder 刚刚经过自注意力处理后的向量。
  - Key 和 Value: 来自阶段一 Encoder 输出的那套固定的 memory 向量。
  - 作用: 这一步是让 Decoder 在决定下一个要生成的词时，去“查阅”和“关注”整个德语输入句子的信息。比如，当它要生成 "I" 时，交叉注意力可能会让它高度关注德语输入中的 "Ich"。
- c. 前馈网络: 经过交叉注意力的结果会被送入前馈网络进行加工。
- d. 预测与采样: 最终预测出下一个词的概率分布，并采样得到新词（比如 "am"）。
- e. 迭代: 将新生成的 "am" 加入到 Decoder 的已知序列中，开始下一轮循环，去生成 "a"。

总结一下 Encoder-Decoder 模型的推理：

模块	作用	何时运行
Encoder	将整个源序列编码成一组固定的 `memory` 向量。	只在最开始运行一次。
Decoder	在一个自回归循环中生成目标序列。	在每个 token 生成时都运行。
↳ 自注意力	让 Decoder 回顾自己已经生成的内容。	在每个生成步骤中运行。
↳ 交叉注意力	让 Decoder 查阅和参考 Encoder 的 `memory`。	在每个生成步骤中运行。
↳ 前馈网络	信息处理。	在每个生成步骤中运行。

面试回答精炼版：

面试官您好，关于推理阶段是否用到 Encoder、Decoder 和交叉注意力，这取决于模型的具体架构：

对于 GPT、Llama 这类 Decoder-Only 模型：它们没有 Encoder，因此推理时只使用 Decoder 部分。生成过程是纯粹的自回归，只涉及到“自注意力”，完全不会用到交叉注意力。
对于原始 Transformer、T5、BART 这类 Encoder-Decoder 模型，通常用于翻译或摘要任务：
- Encoder 和 Decoder 都会用到。 Encoder 在推理开始时运行一次，将输入句子编码成一个固定的 memory。
- Decoder 在一个自回归循环中逐词生成输出。在每一步，它都会用到交叉注意力机制，其 Query 来自 Decoder 自身，而 Key 和 Value 则始终来自于 Encoder 产生的那个固定 memory。这允许 Decoder 在生成每个词时都能参考完整的输入信息。

为什么现在大多是 decoder-only 结构？

问题：为什么现在的大模型大多是 Decoder-Only 结构，而非经典的 Encoder-Decoder 结构？这种结构的优势是什么？原先结构又有哪些劣势？
根本原因：任务范式的统一
传统 Encoder-Decoder 范式：它的设计天生就是为了“序列到序列”（Seq2Seq）任务，比如翻译（德语 -> 英语）、摘要（长文 -> 短文）。它有一个明确的、分离的“源输入”（Source）和“目标输出”（Target）。这种结构在处理这类“转换”任务时非常强大和直观。
现代 LLM (Decoder-Only) 范式：现代大模型的目标是成为一个通用的语言接口，能够处理包括但不限于问答、对话、写作、代码生成、思维链推理等无数种任务。这些任务很多都不是严格的 Seq2Seq 格式。

Decoder-Only 架构通过一个极其简单而强大的范式统一了所有任务：文本补全（Text Completion） 或者说 下一个词预测（Next Token Prediction）。

问答: Q: 什么是引力波？ A: -> 模型补全答案。
翻译: Translate German to English: Ich bin ein Berliner => -> 模型补全 "I am a Berliner."
写代码: // Python function to calculate fibonacci\ndef fib(n): -> 模型补全代码实现。
对话: User: 今天天气怎么样？\nAssistant: -> 模型补全回答。

你看，所有不同的任务都被巧妙地转换成了一个“根据前文预测后文”的统一形式。Decoder-Only 结构正是为这个单一目标而生的，它天生就擅长做“续写”。

1. Decoder-Only 结构的优势

基于上述的范式统一，Decoder-Only 架构展现出几大优势：

架构简单与高效扩展（Simplicity & Scalability）:
- 它只有一个模块（Decoder），结构更统一，实现和维护起来更简单。
- 在训练时，所有参数都为一个统一的“预测下一个词”的目标服务，训练过程更稳定、更直接。
- 这种简单性使得它非常容易进行规模化扩展。当我们把模型从几十亿扩展到几千亿甚至万亿参数时，一个简单、统一的架构是至关重要的。这正是“大力出奇迹”（涌现能力）的基础。
为“上下文学习”（In-Context Learning）而生:
- 这是最核心的优势。Decoder-Only 模型在预测每一个新词时，都会回顾并关注从开头到当前位置的所有上文。这意味着整个提示（Prompt）和已经生成的内容构成了一个动态的、不断增长的上下文。
- 模型学会了从这个上下文中“即时学习”和“领会意图”。你给它几个例子（Few-shot prompting），它就能模仿这个模式；你给它一条指令，它就能理解并执行。这种能力是现代 LLM 如此强大的关键，而 Decoder-Only 的结构天然地支持了这一点。
极佳的生成流畅性:
- 因为它的训练目标和生成方式完全一致（都是自回归地预测下一个词），所以它在生成长篇、连贯、流畅的文本方面表现得非常自然。
1. Encoder-Decoder 结构的劣势（在通用 LLM 场景下）

反过来看，在追求通用模型的背景下，Encoder-Decoder 结构的劣势就显现出来了：

信息瓶颈（Information Bottleneck）与僵化:
- Encoder 将所有源输入信息压缩成一组固定的 memory 向量。尽管 Decoder 可以通过交叉注意力反复查询这个 memory，但这个 memory 本身是一次性生成、静态不变的。
- 相比之下，Decoder-Only 模型在生成每个新词时，它的“上下文”是动态增长的，包含了之前生成的所有内容。这使得它的“世界观”是不断更新的，更加灵活。
架构复杂与训练低效:
- 需要维护和训练两个不同的模块（Encoder 和 Decoder），参数分配和训练动态都更复杂。
- 交叉注意力的引入也增加了计算的复杂性。对于一个统一的、超大规模的模型来说，这种复杂性会成为扩展的阻碍。
不适用于开放式生成与对话:
- 对于没有明确“源输入”的开放式生成任务（比如“写一首关于春天的诗”）或多轮对话，Encoder-Decoder 显得很“笨拙”。我们必须人为地将历史对话或任务指令塞进 Encoder，这远不如 Decoder-Only 模型直接续写来得自然和高效。

简单来说，Encoder-Decoder 模型像是一个专业的“翻译机”或“摘要机”。你给它一个输入，它给你一个精心转换的输出。它非常擅长做特定的“转换”任务。

而 Decoder-Only 大模型则更像一个拥有海量知识、并且精通“阅读理解和模仿续写”的“通才大脑”。你给它任何形式的文本作为开头发动它，它都能理解你的意图，并接着你的话往下说。

随着算力的爆炸式增长，人们发现，把这个“通才大脑”做得足够大，它在完成特定任务时，其效果可以媲美甚至超越那些“专才”模型，同时还具备了前所未有的通用性和灵活性。因此，Decoder-Only 架构成为了通往通用人工智能（AGI）道路上，目前被验证为更优越和更有潜力的选择。

MMoE

当然，混合专家架构（Mixture of Experts, MoE）是当前大模型领域最前沿、最重要的技术之一，尤其在像 Mixtral-8x7B 和 GPT-4（据推测）这样的顶级模型中得到了应用。理解它对于算法岗面试至关重要。

MoE 的核心思路是“用一组专家网络替换模型中的部分全连接网络（FFN），并让一个路由网络（Router）来决定每个输入（Token）应该由哪个或哪些专家来处理”。

这是一种典型的“分治”思想。你可以把它想象成一个大型医院的会诊系统：

传统模型 (Dense Model)：就像一个“全科医生”。无论你是什么病（感冒、骨折、心脏病），你都只能找这一个医生。他什么都懂一点，但对复杂病症可能不够精通。计算开销很大，因为他每次都要调动全部的知识储备来给你看病。
MoE 模型: 就像一个拥有“分诊台”和“多个专科医生”的医院。
- 专科医生 (Experts)：每个医生都是一个独立的前馈网络（FFN），他们分别擅长处理不同类型的信息（比如一个擅长语法，一个擅长事实知识，一个擅长代码逻辑）。
- 分诊台 (Gating Network / Router)：这是一个小型的神经网络。你（一个 Token）来到医院后，分诊台护士会看你的情况（Token 的内容），然后决定把你动态地分配给最相关的一两个专科医生。
- 会诊: 你被送到选定的几个专科医生那里，他们分别给出诊断意见。最后，分诊台会根据之前对你病情的判断，将这几个专家的意见加权汇总，形成最终的诊断报告（Token 的最终输出）。

在训练和推理两侧都会发挥作用，但侧重点和效果不同。

训练阶段:
- 作用: MoE 的主要作用是在保持计算成本（FLOPs）基本不变的情况下，极大地扩展模型的总参数量。
- 解释: 假设一个 dense 模型的 FFN 层有 10B 参数。现在我们用一个 MoE 层替换它，这个 MoE 层包含8个专家，每个专家还是 10B 参数，总参数量就变成了 80B。但在训练时，对于每个 token，路由器只会激活其中的2个专家（Top-2路由）。这意味着这个 token 的计算量只相当于通过了 20B 参数的 FFN，而不是 80B。
- 结果: 我们可以用几乎相同的训练时间和硬件成本，训练出一个总参数量大得多的模型。
- 在训练时，对于每一个 token，模型并不是激活一个大 FFN 里的“部分神经元”，而是从多个独立的 FFN（专家）中，完整地激活一两个来进行计算。不同的 token 可能会被路由到不同的专家组合，这就是所谓的“动态稀疏性”。
推理阶段:
- 作用: MoE 的主要作用是显著提升推理速度。
- 解释: 和训练时一样，在推理时，每个 token 也只会被发送到少数几个被激活的专家那里进行计算。模型虽然总参数量巨大（例如 Mixtral-8x7B 有约47B总参数），但每个 token 推理时实际动用的“活跃参数”只有约13B。
- 结果: 推理速度与一个小的、同等活跃参数量的“稠密模型”相当，但性能却受益于其巨大的总参数量。
有什么效果？解决了什么业界问题呢？

MoE 主要解决了大模型发展中遇到的一个核心矛盾：性能与成本的“不可能三角”。

业界问题（Scaling Law 的诅咒）: 根据大模型的缩放定律（Scaling Laws），模型的性能（如理解、推理能力）与模型的参数量和训练数据量正相关。简单来说，“越大越好”。但是，无限制地增大稠密模型（Dense Model）的规模会遇到瓶颈： 3. 训练成本过高: 训练一个万亿参数的稠密模型需要海量的计算资源和时间，成本高到难以承受。 4. 推理成本过高: 即使训练出来了，让一个万亿参数的稠密模型进行推理，速度会非常慢，延迟极高，无法实际部署应用。

MoE 的解决方案和效果: MoE 通过“稀疏激活”（Sparse Activation）的方式，优雅地绕开了这个难题。

效果一：突破性能瓶颈 它允许模型在可控的计算预算内，将总参数量提升一个甚至多个数量级。更大的参数量意味着更大的模型容量，可以存储更丰富的知识，从而获得更强的“涌现能力”和性能。
效果二：实现高效推理 它让拥有巨大参数量的模型能够以远小于其总规模的计算量进行服务。这就是为什么 Mixtral-8x7B（47B总参数）的推理速度和 Llama 2 13B 差不多，但效果却能媲美 Llama 2 70B。它用更小的推理成本，实现了更强的模型性能。

我对混合专家（MoE）架构的理解如下：

核心思想：MoE 是一种“分治”策略，它用多个专精于不同领域的“专家网络”（独立的FFN）和一个“路由网络”来替换传统模型中的部分全连接层。当一个 token 输入时，路由网络会动态地选择激活少数几个最相关的专家来处理它。
解决的问题：它主要解决了大模型 Scaling Law 下的“性能-成本”矛盾。传统稠密模型越大性能越好，但训练和推理成本会急剧上升，难以承受。
带来的效果：
- 训练时：它可以在计算成本（FLOPs）基本不变的情况下，将模型的总参数量提升数倍，从而让模型拥有更大的容量和潜力。
- 推理时：它通过“稀疏激活”（每个 token 只使用一小部分参数）的方式，使得一个巨大参数量的模型，能够以一个小的稠密模型的速度来进行推理，实现了“低成本，高性能”。

总而言之，MoE 是当前实现超大规模模型、并使其具备实用性的一项关键和前沿的技术。

大模型怎么知道该激活哪几个专家呢？尤其是训练的时候？还是说，路由网络的参数也是训练的一部分？

你的直觉完全正确：路由网络（Gating Network / Router）的参数本身就是模型的一部分，它需要和所有专家以及模型的其他部分一起被训练。

路由网络本身通常是一个非常简单的神经网络，通常就是一个线性层。它的训练过程大致如下：

输入: 对于任意一个 token x（它已经过前面的注意力层处理），路由网络接收 x作为输入。
计算“亲和度”分数: 路由网络内部有一个可训练的权重矩阵 W_g。它将输入 x 与这个权重矩阵相乘，得到一个logit向量，其维度等于专家的数量（比如，8个专家，就得到一个8维的logit向量）。

\[\text{logits} = x \cdot W_g\]

转换为概率/权重: 这个logit向量通过 Softmax 函数，转换成一个概率分布 p。向量 p 中的每一个值 p_i 代表了输入 token x 被分配给第 i 个专家的“权重”或“倾向性”。
```
\[p = \text{Softmax}(\text{logits})\]
```
做出路由决策 (Top-K Gating):
- 模型选择 p 中值最大的 K 个（比如K=2）。
- 被选中的这 K 个专家被激活。
- 这 K 个专家对应的概率值 p_i 将被用作后续结果加权的权重。
计算与反向传播:
- Token x 被送到这 K 个被激活的专家那里进行计算。
- 其他未被选中的专家则完全不参与计算。
- 在得到最终输出后，当计算模型的总损失（Loss）并进行反向传播时，梯度不仅会流向被激活的专家，让它们学习如何更好地处理这类 token，同时梯度也会流回路由网络，更新它的权重矩阵 W_g。

关键点：通过这个过程，路由网络 W_g 就会慢慢学会：“哦，当看到一个像 x 这样的 token（比如一个 Python 关键词），我应该把它分配给第3号和第7号专家（可能它们已经逐渐专精于代码），并且分配给第3号专家 70% 的权重，第7号专家 30% 的权重。”

一个巨大的挑战：负载不均衡 (Load Imbalance)

如果单纯这样训练，会很容易出现一个严重问题：“马太效应”。

路由器可能会很快发现有几个专家特别“能干”（或者只是初始参数比较好），于是倾向于把所有类型的 token 都发给这几个“明星专家”。这会导致： * 明星专家过载: 少数专家被过度训练，计算负载集中。 * 懒汉专家荒废: 其他专家很少接收到 token，得不到训练，其参数基本不变，逐渐“荒废”。

这违背了我们希望专家们“各有所长、分工合作”的初衷。

解决方案：负载均衡损失 (Load Balancing Loss)⚓︎

为了解决这个问题，研究者引入了一种巧妙的辅助损失函数 (Auxiliary Loss)，专门用来“惩罚”不均衡的路由行为。

这个损失函数的设计目标是鼓励路由器将 token 尽可能均匀地分配给所有专家。

它的计算方式大致是：

在一个批次（Batch）的训练中，统计每个专家被分配到的 token 数量的比例。
如果这个分配非常不均匀（比如专家1处理了90%的token，其他7个专家只处理了剩下的10%），那么负载均衡损失就会变得非常大。
这个辅助损失会与模型的主要损失（比如预测下一个词的交叉熵损失）加在一起，共同指导模型的训练。

$$ \text{Total Loss} = \text{Main Loss} + \alpha \times \text{Load Balancing Loss} $$ （其中 α 是一个超参数，用来控制这个辅助损失的重要性）

通过这种方式，路由器在训练时就陷入了一种“甜蜜的烦恼”： * 一方面，它想把 token 送给最匹配的专家，以降低主要损失。 * 另一方面，它又必须顾及公平，尽量雨露均沾地把 token 分给所有专家，以降低辅助损失。

在这种权衡之下，模型最终会学到一个既高效又均衡的路由策略，促使不同的专家群体逐渐演化出处理不同领域知识的“专长”。

面试总结

面试官您好，关于MoE如何学习路由，我的理解是：

路由网络本身是可训练的：它是一个小型神经网络（通常是线性层），其参数是整个大模型参数的一部分，会在训练中通过反向传播进行学习。
学习机制：在训练时，对于每个token，路由网络会计算并输出一个分配给所有专家的“权重”或“概率”，并选择权重最高的几个专家激活。当模型根据最终预测结果计算损失并反向传播时，梯度也会更新路由网络的参数，从而让它学会“看到什么类型的token，就该分配给哪些专家”。
核心挑战与解决方案：这个学习过程面临“负载不均衡”的挑战，即路由器可能倾向于只使用少数几个专家。解决方案是引入一个“负载均衡辅助损失函数”。这个额外的损失会惩罚不均衡的分配行为，迫使路由器在追求“专业对口”的同时，也要尽量“雨露均沾”，从而激励所有专家都得到充分训练，最终形成各有所长的分工体系。

BF16、FP16、FP32对比

澄清概念：首先，FP32、FP16、BF16都是浮点数格式，将模型从高精度转为低精度浮点数的过程通常叫低精度或混合精度训练。而“量化”在业界通常特指将模型从浮点数转为INT8/INT4等整数格式，主要用于推理加速。

核心作用：使用这些低精度格式的核心目的是为了解决大模型的“内存墙”和“计算墙”问题。具体来说，它们能：

节省显存：将模型权重从32位减为16位，显存占用直接减半。加快计算：数据传输更快，并且现代GPU的Tensor Core对16位计算有专门优化，速度远超32位。不同格式的权衡（Trade-off）：

FP32是基准，精度高但开销大。 FP16牺牲了动态范围来保留部分精度。这导致它在训练时梯度容易溢出，稳定性差，需要配合混合精度等复杂技巧。 BF16的设计非常关键，它保留了和FP32完全相同的动态范围，只牺牲了精度。这使得它在训练时非常稳定，几乎可以直接替代FP32，因此成为了当前大模型训练的主流选择。 INT8/INT4量化是更极致的压缩，主要用在推理阶段，以最大化地降低模型体积和延迟，方便在消费级硬件上部署，但会伴随一定的精度损失。总结来说，这是一个典型的用精度换取效率的策略。BF16因为其出色的训练稳定性，成为了平衡性能和成本的最佳甜点，而INT量化则是端侧部署的终极武器。

Embedding⚓︎

词嵌入，NLP 的常用技术。

class InputEmbeddings(nn.Module):

    def __init__(self, d_model: int, vocab_size: int) -> None:
        super().__init__()
        self.d_model = d_model # 模型的embedding 的维度 (512)
        self.vocab_size = vocab_size 
        self.embedding = nn.Embedding(vocab_size, d_model)
        # embedding 本质上是把一个表示 token 的索引映射到向量中

    def forward(self, x):
        # (batch, seq_len) --> (batch, seq_len, d_model)
        # Multiply by sqrt(d_model) to scale the embeddings according to the paper
        # embedding 的结果需要进行缩放
        return self.embedding(x) * math.sqrt(self.d_model)

Positional Embedding⚓︎

Transformer 中的位置编码，传递每个Token在上下文中的位置信息，维度和 embedding 一样，遵循：

$PE(pos, 2i) = \sin \dfrac{pos}{10000^{\frac{2i}{d_{model}}}}$

$PE(pos, 2i + 1) = \cos \dfrac{pos}{10000^{\frac{2i + 1}{d_{model}}}}$

对于上下文中每个位置的 embedding，根据embedding的索引奇偶给出对应的计算。

class PositionalEncoding(nn.Module):

    def __init__(self, d_model: int, seq_len: int, dropout: float) -> None:
        super().__init__()
        self.d_model = d_model
        self.seq_len = seq_len # 上下文的长度
        self.dropout = nn.Dropout(dropout) # Dropout: 减少过拟合
        # Create a matrix of shape (seq_len, d_model) 
        pe = torch.zeros(seq_len, d_model) # 所有上下文每个位置的 RoPE 的矩阵
        # Create a vector of shape (seq_len)
        position = torch.arange(0, seq_len, dtype=torch.float).unsqueeze(1) # (seq_len, 1)
        # Create a vector of shape (d_model)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model)) # (d_model / 2)
        # Apply sine to even indices
        pe[:, 0::2] = torch.sin(position * div_term) # sin(position * (10000 ** (2i / d_model))
        # Apply cosine to odd indices
        # 这里的 even / odd indices 是 embedding 的 even / odd 位置的参数
        # 这里的 position 是这个 token 在上下文中的位置
        pe[:, 1::2] = torch.cos(position * div_term) # cos(position * (10000 ** (2i / d_model))
        # Add a batch dimension to the positional encoding
        # 添加一个 batch 维度方便后面训练
        pe = pe.unsqueeze(0) # (1, seq_len, d_model)
        # Register the positional encoding as a buffer
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + (self.pe[:, :x.shape[1], :]).requires_grad_(False) # (batch, seq_len, d_model)
        # positional embedding 的部分不需要计算梯度 直接加到 embedding 层上即可
        return self.dropout(x)

好的，位置编码是 Transformer 中一个极其精妙的设计，而 RoPE 的出现更是现代大语言模型（LLM）性能提升的关键之一。理解它们的区别是面试中的一个高频考点。

我们来详细对比一下这两种位置编码方式。

核心问题：为什么要位置编码？

Transformer 的自注意力机制本身是置换不变的（Permutation-Invariant）。也就是说，如果你打乱输入句子中词的顺序，注意力层的输出是完全一样的，因为它只关心词与词之间的关系，不关心谁在谁前面。这显然不符合自然语言的规律，因此必须引入一种方法来告诉模型每个词的绝对或相对位置。

Sinusoidal Positional Encoding⚓︎

这是 "Attention Is All You Need" 论文中提出的原始方案，也就是 “绝对位置编码”。

它为序列中的每一个绝对位置（如第1个词、第2个词...）生成一个固定的、唯一的向量，然后将这个位置向量加到对应位置的词嵌入向量上。

做法 (How it works):

生成位置向量：对于位置为 pos、维度为 i 的分量，其编码值通过 sin 和 cos 函数计算得出：
- 当 i 是偶数时： $PE_{(pos, 2i)} = \sin(pos / 10000^{2i/d_{model}})$
- 当 i 是奇数时： $PE_{(pos, 2i+1)} = \cos(pos / 10000^{2i/d_{model}})$
其中，$pos$ 是词在序列中的位置（0, 1, 2, ...），$i$ 是维度的索引（0, 1, 2, ...），$d_{model}$ 是词嵌入的总维度。
集成方式：将生成的固定位置向量 $PE$ 直接加到输入的词嵌入向量 $X_{embedding}$ 上。 $$ X_{final} = X_{embedding} + PE $$ 这个新的 $X_{final}$ 向量既包含了词的语义信息，也包含了词的绝对位置信息。

优点1 (固定且可外推)：它是通过公式计算得到的，不需要训练。理论上，它可以生成任意长度序列的位置编码，具备一定的外推能力。
优点2 (隐含相对位置)：论文作者证明，对于任意固定的偏移量 $k$， $PE_{pos+k}$ 可以表示为 $PE_{pos}$ 的一个线性变换。这意味着模型有潜力从绝对位置编码中学习到相对位置关系。
缺点 (间接与混合)：模型需要自己学习去理解这种通过 sin/cos 编码的相对位置信息，这是一种间接的方式。更重要的是，通过加法将位置信息和语义信息混合在一起，可能会在一定程度上“污染”原始的语义表示。

为什么要用 sin， cos 三角函数？

这个设计非常巧妙，主要利用了三角函数的性质：

唯一性：对于每个位置 $pos$，它都会生成一个独一无二的位置向量。有界性：sin 和 cos 的值域在 [-1, 1] 之间，使得位置编码的值不会过大或过小，有利于模型训练的稳定性。

核心特性：蕴含相对位置信息：这是最关键的一点。一个位置为 $pos+k$ 的位置向量 $PE_{pos+k}$，可以被表示为位置为 $pos$ 的向量 $PE_{pos}$ 的一个线性变换。这意味着，模型可以轻易地学习到 token 之间的相对位置关系。例如， Attention 机制可以学会“关注距离当前词前面4个位置的词”，因为不同位置之间的这种“距离关系”在向量空间中是有规律的。

RoPE:Rotary Positional Embedding⚓︎

RoPE 的思想非常优雅：通过向量旋转的方式，将相对位置信息集成到注意力计算中。它不改变词向量本身，而是在计算 Attention Score 的时候（Q、K 点积时）引入位置信息。

RoPE 不直接修改词嵌入。它等到 Q 和 K 向量生成之后，再对其进行操作。

向量旋转：将 $d$ 维的 Q 和 K 向量，两两一组（例如 $(q_0, q_1), (q_2, q_3), ...$）看作是在二维平面上的向量（或者说看作复数）。然后将每个二维向量都旋转一个角度 $\theta_m$，这个角度 $\theta_m$ 与词的位置 $m$ 相关。
- 对于位置为 $m$ 的词向量 $q_m$，其旋转操作可以用一个旋转矩阵 $R_m$ 来表示：
```
\[
q'_m = R_m q_m
\]
```
  这个操作会施加在 Q 和 K 向量上，但不会施加在 V 向量上。
神奇的内积：经过旋转后，两个位置 $m$ 和 $n$ 上的新 Query 向量 $q'_m$ 和新 Key 向量 $k'_n$ 的内积，会神奇地只与它们的相对位置 $(m-n)$ 和原始的 $q, k$ 向量相关，而与它们的绝对位置 $m, n$ 无关。

数学上可以证明：
```
\[
(q'_m)^T k'_n = (R_m q_m)^T (R_n k_n) = \text{一个只依赖于 } (q_m, k_n) \text{ 和 } (m-n) \text{ 的函数}
\]
```
这就意味着，注意力分数天然地就包含了相对位置信息！

它通过旋转操作，直接将相对位置信息编码进了 Attention 的计算过程里。

效果/特点

优点1 (显式的相对位置编码)：RoPE 直接在注意力分数计算中注入了相对位置信息。模型不需要“学习”去理解相对位置，而是直接利用它。这更加直观和高效。
优点2 (更好的外推性)：由于其相对位置的性质，RoPE 在处理比训练时更长的序列时，表现出了非常好的外推性能（即泛化到未见过的长度）。
优点3 (不改变语义信息)：旋转操作只改变向量的方向，不改变其模长（L2 Norm）。这意味着它在引入位置信息的同时，不会像加法那样改变词向量本身的语义强度。
成为主流：正是因为这些优异的性质，RoPE 成为了当前最先进的 Decoder-Only LLM 的事实标准。

特性	三角函数绝对位置编码 (Sinusoidal PE)	RoPE 旋转位置编码
本质	绝对位置编码 (Absolute)	相对位置编码 (Relative, in essence)
注入方式	加法 (Additive)：直接加在词嵌入上	乘法 (Multiplicative)：通过旋转矩阵修改Q和K
作用对象	词嵌入向量 (Token Embedding)	Query 和 Key 向量（在Attention计算中）
相对位置	间接学习：模型需要从绝对位置的线性关系中学习相对位置	直接注入：内积结果天生只与相对位置有关
是否可学习	否，是固定公式计算	否，是固定公式计算
核心优势	简单，无参数	天然携带相对位置关系，外推性好，不改变语义模长
当前应用	早期 Transformer 模型 (如 BERT)	主流大模型 (LLaMA, PaLM, GLM 等)

LayerNorm⚓︎

相当于在特征维度的归一化。

具体讲，在 Transformer 中，Layer Norm 是对Attention层输出的整个 seq_len * d_model 矩阵进行归一化。

Layer Norm 的 "Layer" 指的是一个样本在当前层的所有激活值。在 Transformer 的这个场景下，一个样本的“层”就是指整个 seq_len * d_model 的矩阵。

输入: 一个 [seq_len, d_model] 的矩阵。
操作:
1. 将这个 seq_len * d_model 矩阵看作一个大的向量，或者说，计算所有 seq_len * d_model 个元素的总均值 $\mu_{total}$ 和总方差 $\sigma_{total}^2$。
2. 这里你只会得到一个均值和一个方差。
3. 使用这对全局的 $(\mu_{total}, \sigma_{total})$ 来归一化矩阵中的每一个元素。

具体步骤：

输入: 矩阵 $X$，维度为 [seq_len, d_model]。

计算统计量:

\[
\mu = \frac{1}{\text{seq\_len} \times d_{model}} \sum_{i=1}^{\text{seq\_len}} \sum_{j=1}^{d_{model}} X_{ij}
\]

\[
\sigma^2 = \frac{1}{\text{seq\_len} \times d_{model}} \sum_{i=1}^{\text{seq\_len}} \sum_{j=1}^{d_{model}} (X_{ij} - \mu)^2
\]

注意：这里只有一个 $\mu$ 和一个 $\sigma$。

归一化: 对矩阵 $X$ 中的每一个元素 $X_{ij}$ 进行归一化：
```
\[
\hat{X}_{ij} = \frac{X_{ij} - \mu}{\sqrt{\sigma^2 + \epsilon}}
\]
```
缩放与偏移: 最后，引入两个可学习的参数，gamma ($\gamma$) 和 beta ($\beta$)。这两个参数的维度通常是 d_model。它们的作用是让模型能够恢复一部分归一化操作可能丢失的表示能力。
```
\[
Y_{ij} = \gamma_j \cdot \hat{X}_{ij} + \beta_j
\]
```
注意，这里的 $\gamma$ 和 $\beta$ 是按特征维度（d_model）广播的。第 j 个特征维度的所有元素，都使用相同的 $\gamma_j$ 和 $\beta_j$ 进行缩放和偏移。

这样做的直觉：

将整个 seq_len * d_model 矩阵一起归一化，其背后的直觉是：对于单个训练样本，在经过一个层（如自注意力层）的计算后，我们希望整个输出的分布是稳定的，而不仅仅是每个 token 的表示是独立的稳定。这种方式将整个序列的表示视为一个整体来进行控制，有助于稳定深层模型的训练动态，防止梯度爆炸或消失，这在实践中被证明是非常有效的。

我们来看一个 batch_size=1, seq_len=4, d_model=3 的例子。

输入矩阵 X (4x3):

[[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[0, 1, 2]]

你的理解 (Row Norm): 1. 对 [1, 2, 3] 计算均值和方差，归一化这一行。 2. 对 [4, 5, 6] 计算均值和方差，归一化这一行。 3. ...

实际的 Layer Norm: 1. 对所有12个数字 [1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2] 计算一个总均值 $\mu$ 和一个总方差 $\sigma^2$。 * $\mu = (1+2+...+9+0+1+2) / 12 = 4.0$ * ...计算 $\sigma^2$ 2. 用这对 $(\mu, \sigma)$ 去归一化这12个数字中的每一个。

同样的，这里归一化的参数也是可以学习的。

class LayerNormalization(nn.Module):

    def __init__(self, features: int, eps:float=10**-6) -> None:
        super().__init__()
        self.eps = eps
        self.alpha = nn.Parameter(torch.ones(features)) # alpha is a learnable parameter
        self.bias = nn.Parameter(torch.zeros(features)) # bias is a learnable parameter

    def forward(self, x):
        # x: (batch, seq_len, hidden_size)
         # Keep the dimension for broadcasting
        mean = x.mean(dim = -1, keepdim = True) # (batch, seq_len, 1)
        # 相当于,每个上下文中,每一个位置 (第1, 2, ,3 ... , 512个位置的embedding做了一个Normalization)
        # Keep the dimension for broadcasting
        std = x.std(dim = -1, keepdim = True) # (batch, seq_len, 1)
        # eps is to prevent dividing by zero or when std is very small
        # 归一化的参数 (一个是乘积,一个是累加的bias）都是可以学习的
        return self.alpha * (x - mean) / (std + self.eps) + self.bias

Why not Batch Norm?⚓︎

简短的回答是：因为 Transformer 处理的是变长的序列数据，Layer Normalization (LN) 独立于批次大小（Batch Size）和序列长度，对每个样本独立进行归一化，非常适合 NLP 任务；而 Batch Normalization (BN) 依赖于整个批次的统计信息，对于变长的文本序列适应性很差，并且在小批量下表现不稳定。

比如，同一个批次，同一个位置，可能有很多文本Token都是空白，填补了 PAD。这导致整个 Batch 的方差过大，训练不稳定。

下面我们来详细拆解这个答案，这也是你在面试时应该展示的深度。

Normalization 的目标是解决“内部协变量偏移”（Internal Covariate Shift）问题，Batch Norm 对一个 mini-batch 内的同一个特征（channel）进行归一化。

操作对象：给定一个批次的数据，维度为 [N, L, D] (批次大小, 序列长度, 特征维度)。
计算方式：BN 会选择第 d 个特征（d from 1 to D），然后计算这个特征在所有 N 个样本和所有 L 个位置上的均值和方差，用这个均值和方差来归一化所有样本的第 d 个特征。
核心：跨样本（Across Samples） 进行归一化。

在 Transformer (NLP) 中的局限性

对可变序列长度的适应性极差（最主要原因）：
- NLP 任务中的句子长度千差万别。一个批次中可能既有 10 个词的短句，也有 500 个词的长句。
- 如果一个批次里的句子都用 <pad> 符号填充到相同长度，那么在计算 BN 的均值和方差时，这些填充的 <pad> 符号也会被计入统计，这会引入大量的噪声，严重影响归一化效果。
- 即使不填充，如何对齐不同长度序列的同一“位置”的特征并计算其统计量也是一个非常棘手且不自然的问题。比如，批次中第一个句子的第 10 个词和第二个句子的第 10 个词，它们的语义和统计特性可能完全不同。
对小批量大小（Small Batch Size）敏感：
- Transformer 模型（尤其是大型语言模型）通常非常大，占用大量 GPU 显存。这迫使我们在训练时只能使用很小的批次大小（有时甚至为 1）。
- BN 严重依赖批次大小来获得稳定、有代表性的统计数据（均值和方差）。当批次很小时，计算出的均值和方差会有很大的噪声，导致模型训练不稳定，性能下降。
训练和推理时的行为不一致：
- BN 在训练时使用当前批次的统计数据，在推理时则使用在整个训练集上计算出的滑动平均值。这种不一致性为模型实现和部署增加了一丝复杂性。

Layer Normalization 为了解决 BN 对批次大小的依赖，改变了归一化的维度。它对同一个样本内的所有特征进行归一化。

操作对象：给定一个批次的数据，维度为 [N, L, D]。
计算方式：LN 会选择第 n 个样本（n from 1 to N），然后计算这个样本在所有 L 个位置和所有 D 个特征维度上的均值和方差，用这个均值和方差来归一化这一个样本自身。
核心：样本内部（Within a Sample）进行归一化，完全独立于批次中的其他样本。

在 Transformer 中的优势

完美适应可变序列长度：
- 因为 LN 是对单个样本进行操作，所以一个样本是长是短，或者批次中其他样本是长是短，都完全不影响对当前样本的归一化计算。每个样本都有自己的均值和方差。
不依赖于批次大小：
- LN 的计算完全在样本内部，与批次大小无关。即使批次大小为 1，也能进行稳定有效的归一化。这对于训练大型 Transformer 模型至关重要。
训练和推理时行为一致：
- 无论在训练还是推理，LN 的计算方式都是一样的，都是对当前输入样本进行归一化，不需要像 BN 那样维护一个全局的滑动平均值。这使得模型行为更具确定性，实现也更简单。

Comparison⚓︎

特性	Batch Normalization (BN)	Layer Normalization (LN)
归一化方向	对一个特征在整个批次上归一化	对一个样本在所有特征上归一化
依赖性	强依赖批次大小	完全独立于批次大小
对变长序列	适应性差，填充符会引入噪声	完美适应，每个样本独立计算
使用场景	图像（CNN），特征分布相对稳定	序列数据（RNN, Transformer）
训练/推理	行为不一致	行为一致

你提出的这个追问非常精准，它让你从“为什么A不适合”的被动理解，转向了“为什么B适合”的主动理解，形成了知识的闭环。

你的初始回答非常正确。现在，我们来深入探讨你的追问：Batch Norm (BN) 一般用在什么任务上？为什么它在这些任务上表现优异？

Batch Norm: CV (🤔)⚓︎

如果你看到一个现代非 Transformer 架构的卷积神经网络 (Convolutional Neural Network, CNN)，比如 ResNet, VGG, Inception, EfficientNet 等，你几乎总能在它的卷积层和全连接层之间找到 Batch Norm 的身影。

BN最主要和最成功的应用领域是计算机视觉，涵盖了以下任务：

图像分类 (Image Classification)
目标检测 (Object Detection)
图像分割 (Image Segmentation)
图像生成 (Image Generation) (在生成器中)

这主要源于 CV 任务中数据（图像）的特性与 BN 的工作原理高度契合。

数据特性：固定的输入尺寸和通道独立性 (Fixed Size & Channel Independence)

这是最根本的原因。

图像处理的范式：在输入到一个 CNN 之前，无论原始图像大小如何，它们通常都会被缩放或裁剪到一个固定的尺寸，例如 224x224 像素。
数据表示：一批 (Batch) 图像的数据张量通常表示为 [N, C, H, W]：
- N: 批次大小 (Batch Size)
- C: 通道数 (Channels, 如_R_G_B_为3)
- H: 高度 (Height)
- W: 宽度 (Width)
BN 的工作方式：BN 的计算是沿着 N, H, W 这三个维度进行的，而为每一个通道 C 独立计算均值和方差。

BN 旨在问这样一个问题：“对于这一批所有图像的同一个通道（比如蓝色通道），所有像素位置的平均激活值和方差是多少？”

这个提问基于如下的假设：

空间相关性：图像中的一个像素和它周围的像素是有关系的。
统计一致性：对于一个大规模、经过良好洗牌的图像数据集（比如 ImageNet），一批猫的图片和另一批猫的图片，在统计特征上是相似的。因此，用一批数据的均值/方差去近似整个数据集的均值/方差是合理的。

这和 NLP 任务形成了鲜明对比。在 NLP 中，句子是变长的，你无法对一批句子中“第10个词”的向量做统计，因为句子A的第10个词（比如“的”）和句子B的第10个词（比如“猫”）毫无关联。而一批图像的“第(10,10)个像素”则很可能都属于背景或某个物体的一部分，它们的统计量是有意义的。

大批量训练 (Large Batch Sizes) 的可行性

统计的稳定性：BN 的效果很大程度上取决于批次统计量对全局统计量的近似程度。批次越大 (Large Batch)，这个近似就越准确，训练就越稳定。
CV 训练的实践：在 CV 领域，得益于 GPU 并行计算的优化，使用较大的 Batch Size (如 64, 128, 256...) 是常规操作。这为 BN 提供了表现优异的土壤。
反面例子：当 Batch Size 很小（比如2或4）时，批次的均值和方差会剧烈波动，这反而会给模型带来噪声，导致训练不稳定。这也是为什么在某些显存受限的场景（如高分辨率图像分割）下，人们会用其他归一化方法（如 Group Normalization）替代 BN。

解决内部协变量偏移 (Internal Covariate Shift, ICS)

这也是 BN 论文中提出的核心动机。深层网络的每一层都在学习，导致其输出的数据分布在训练过程中不断变化。对于下一层来说，它的输入分布一直在“漂移”，这使得学习变得困难。

BN 通过在每一层强制将输入数据归一化到均值为0，方差为1的稳定分布，极大地缓解了这个问题，带来了两大好处： * 可以使用更高的学习率，加速模型收敛。 * 降低了对参数初始化的敏感度，让训练更加容易。

Feed Forward Network (FFN)⚓︎

其实是两个通过ReLU连接的全连接层，对 embedding 进行学习。

class FeedForwardBlock(nn.Module):
    # Feedforward Network,本质上是两个全连接层，激活函数用ReLU连接
    # "applied to each position separately and identically"
    # FFN(x) = max(0, xW_1 + b_1)W_2 + b_2
    def __init__(self, d_model: int, d_ff: int, dropout: float) -> None:
        super().__init__()
        self.linear_1 = nn.Linear(d_model, d_ff) # w1 and b1
        self.dropout = nn.Dropout(dropout)
        self.linear_2 = nn.Linear(d_ff, d_model) # w2 and b2


    def forward(self, x):
        # 先把每个位置的 embedding 传递到 dff (=2048) 维度的全连接层，然后再连接回 512 (d_model)
        # (batch, seq_len, d_model) --> (batch, seq_len, d_ff) --> (batch, seq_len, d_model)
        return self.linear_2(self.dropout(torch.relu(self.linear_1(x))))

为什么需要这一层？

简单来说，FFN 的核心作用有两个：

增加非线性变换：这是最根本和最重要的作用。
进行表示空间的转换和提炼：对注意力层聚合后的信息进行进一步的加工和筛选。

让我们来详细探讨一下。

为什么“非线性”如此重要？

首先，我们回顾一下注意力层的核心计算。它的输出本质上是输入值（Values）的一个加权平均和。

\[
\text{Attention output} = \sum_{i} \text{weight}_i \cdot \text{Value}_i
\]

尽管权重（weight）的计算（通过 softmax）是非线性的，但对于 Value 向量来说，最终的操作是一个线性组合。如果你连续堆叠多个只有注意力层的模块（即使是多头的），整个模型的大部分计算仍然是线性的变换序列。而多个线性变换的堆叠其效果等价于一个单独的线性变换。

这意味着，如果没有 FFN 引入的非线性激活函数（通常是 ReLU 或 GELU），Transformer 无论堆叠多少层，其表达能力都会受到极大限制，本质上仍然是一个（非常复杂的）线性模型。它将无法学习数据中存在的复杂模式和非线性关系，比如语言中复杂的语法、逻辑和语义关系。

所以，FFN 引入的非线性激活函数是模型“深度”之所以有效的关键。

FFN 的具体结构和作用：“处理和提炼”信息

FFN 通常是一个由两个线性层（全连接层）和它们之间的一个非线性激活函数组成的小网络。它作用于序列中的每一个位置（Position-wise）。

\[
\text{FFN}(x) = \text{Linear}_2(\text{ReLU}(\text{Linear}_1(x)))
\]

或者用权重和偏置更详细地表示：

\[
\text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2
\]

这里有几个关键点： * Position-wise: 这个 FFN 是独立地应用于序列中每个 token 的表示向量上的。也就是说，所有位置的 token 共享同一套 FFN 的权重（$W_1, b_1, W_2, b_2$），但每个 token 的计算是独立的，不与其他 token 发生信息交换。 * 维度变换: * 第一个线性层 Linear_1 通常会将输入的维度 $d_{model}$ 扩展到一个更高的维度 $d_{ff}$（在原始 Transformer 论文中，$d_{model}=512, d_{ff}=2048$，是4倍关系）。 * 第二个线性层 Linear_2 再把维度从 $d_{ff}$ 投影回 $d_{model}$。

这种 “扩展->非线性激活->压缩” 的结构非常巧妙。我们可以把它理解为一个特征提炼器或信息处理中心。

来自Gemini的比喻：会议室里的讨论与个人思考

我们可以把一个 Transformer Block 想象成一次高效的会议决策过程：

多头注意力层 (Multi-Head Attention)：这相当于会议的全员讨论环节。每个人（token）都会听取所有其他与会者的发言（Values），并根据与自己的相关性（Q-K 匹配度）来决定重点吸收哪些信息。会议讨论结束后，每个人脑子里都形成了一个融合了全场信息的、新的综合性想法（Attention Output）。
前馈神经网络 (Feed-Forward Network)：这相当于会议讨论后的个人独立思考和整理环节。每个人回到自己的工位上，对自己刚刚吸收到的海量综合信息进行处理。
- 扩展（Up-project to $d_{ff}$）：他/她会把这个综合性想法发散开，在脑内一个更广阔的“思维空间”里，去分析和联想所有可能的方面和潜在的特征组合。
- 非线性激活（ReLU/GELU）：在这个过程中，他/她会过滤掉那些不重要、不相关或者冗余的想法（比如 ReLU 会将负值部分直接置为0）。
- 压缩（Down-project to $d_{model}$）：最后，他/她把这些经过深思熟虑、筛选和提炼后的精华观点，重新总结成一个标准格式的、清晰的结论（变回 $d_{model}$ 维度），准备提交给下一轮会议（下一个 Transformer Block）。

总结：为什么必须有 FFN？

从功能互补上看：Attention 层负责在序列内的不同 token 之间横向交换和聚合信息。而 FFN 层则负责对每个 token 自身的表示进行纵向的深度加工和非线性变换。两者分工明确，缺一不可。Attention 负责“沟通”，FFN 负责“计算/思考”。
从模型能力上看：没有 FFN，Transformer 就失去了深度学习模型最关键的非线性建模能力，其性能将大打折扣。FFN 提供的维度扩展和非线性激活，极大地增强了模型的参数容量和拟合复杂函数的能力。

FFN 和 Attention 是 Transformer 中相辅相成的两个核心组件。Attention 解决了长距离依赖和信息交互问题，而 FFN 则赋予了模型强大的非线性表示学习能力，使得对这些交互信息进行深度加工成为可能。

Multi-Head Attention (MHA)⚓︎

class MultiHeadAttentionBlock(nn.Module):

    def __init__(self, d_model: int, h: int, dropout: float) -> None:
        super().__init__()
        self.d_model = d_model # Embedding vector size
        self.h = h # Number of heads, 不同头的数量
        # Make sure d_model is divisible by h
        assert d_model % h == 0, "d_model is not divisible by h"

        self.d_k = d_model // h # Dimension of vector seen by each head
        self.w_q = nn.Linear(d_model, d_model, bias=False) # Wq (batch, d_model, d_model)
        self.w_k = nn.Linear(d_model, d_model, bias=False) # Wk
        self.w_v = nn.Linear(d_model, d_model, bias=False) # Wv
        self.w_o = nn.Linear(d_model, d_model, bias=False) # Wo
        self.dropout = nn.Dropout(dropout)
        # 每个头都只能看到对应的向量 (embedding 的部分)

    @staticmethod
    def attention(query, key, value, mask, dropout: nn.Dropout):
        d_k = query.shape[-1]
        # Just apply the formula from the paper
        # (batch, h, seq_len, d_k) --> (batch, h, seq_len, seq_len)
        attention_scores = (query @ key.transpose(-2, -1)) / math.sqrt(d_k)
        if mask is not None:
            # Write a very low value (indicating -inf) to the positions where mask == 0
            attention_scores.masked_fill_(mask == 0, -1e9)
        attention_scores = attention_scores.softmax(dim=-1) # (batch, h, seq_len, seq_len) # Apply softmax
        if dropout is not None:
            attention_scores = dropout(attention_scores)
        # (batch, h, seq_len, seq_len) --> (batch, h, seq_len, d_k)
        # return attention scores which can be used for visualization
        return (attention_scores @ value), attention_scores

    def forward(self, q, k, v, mask):
        query = self.w_q(q) # (batch, seq_len, d_model) --> (batch, seq_len, d_model)
        key = self.w_k(k) # (batch, seq_len, d_model) --> (batch, seq_len, d_model)
        value = self.w_v(v) # (batch, seq_len, d_model) --> (batch, seq_len, d_model)

        # (batch, seq_len, d_model) --> (batch, seq_len, h, d_k) --> (batch, h, seq_len, d_k)
        query = query.view(query.shape[0], query.shape[1], self.h, self.d_k).transpose(1, 2)
        key = key.view(key.shape[0], key.shape[1], self.h, self.d_k).transpose(1, 2)
        value = value.view(value.shape[0], value.shape[1], self.h, self.d_k).transpose(1, 2)

        # Calculate attention
        x, self.attention_scores = MultiHeadAttentionBlock.attention(query, key, value, mask, self.dropout)

        # Combine all the heads together
        # (batch, h, seq_len, d_k) --> (batch, seq_len, h, d_k) --> (batch, seq_len, d_model)
        x = x.transpose(1, 2).contiguous().view(x.shape[0], -1, self.h * self.d_k)

        # Multiply by Wo
        # (batch, seq_len, d_model) --> (batch, seq_len, d_model)  
        return self.w_o(x)

注意力层的本质功能/本质作用是什么？

注意力层的作用是，为句子中的每个词动态地生成一个“上下文相关的”表示，其方法是计算这个词与句子中所有其他词的相关性分数，并据此对所有词的信息进行加权求和。

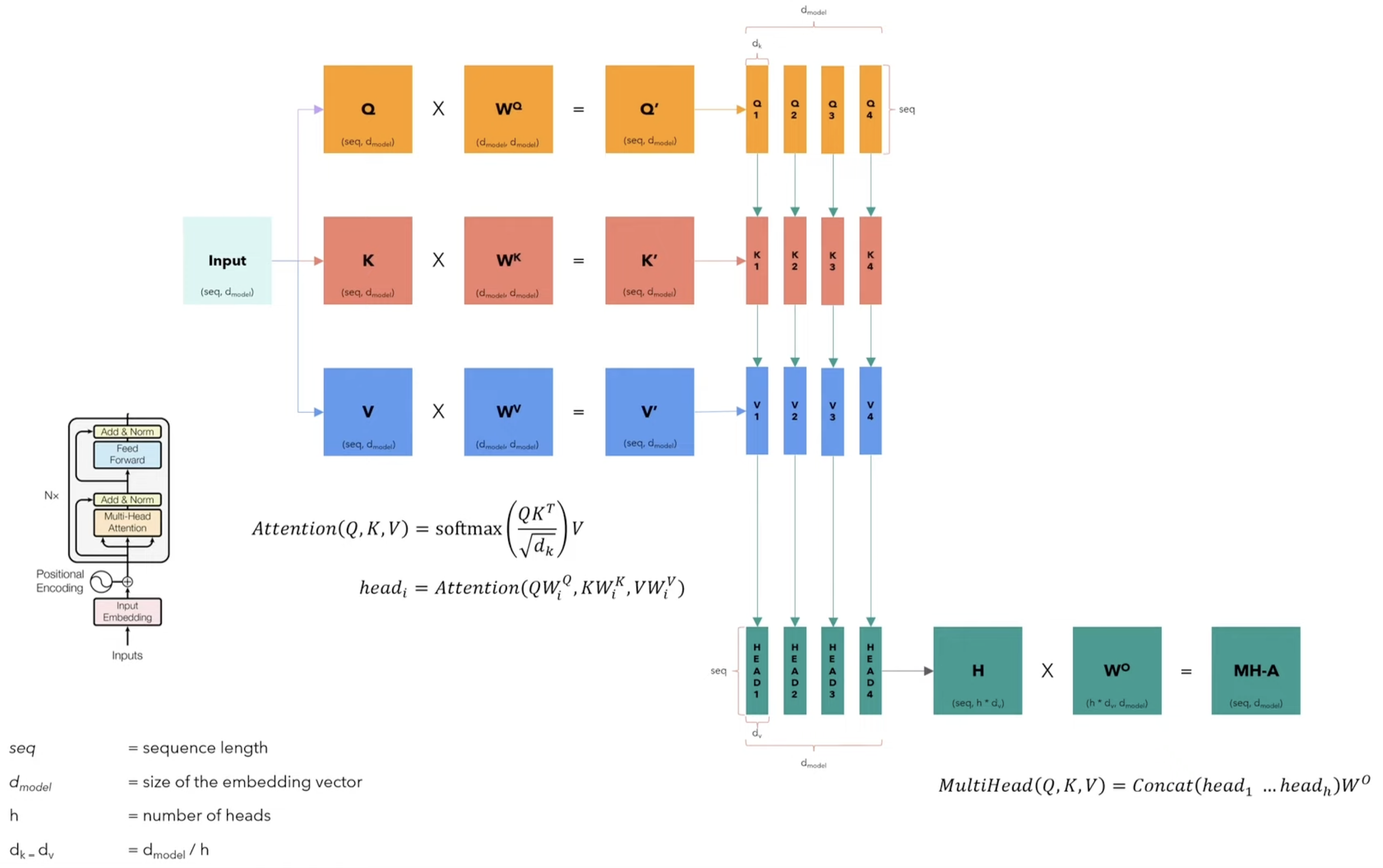
比如，公式 $\text{softmax} (\dfrac{QK^T}{\sqrt{d_k}}) V$，每一步的作用：

计算相关性：当前词的 Query 会和所有词的 Key 进行一次匹配计算（通常是点积），得出一个“相关性分数”。这个分数越高，说明这个词与当前词越相关。
权重归一化：使用 Softmax 函数将这些分数转换成一组总和为1的权重。这些权重就是“注意力分布”。
加权求和：用这些权重去乘以所有词对应的 Value，然后把它们加起来。

其优势功能是：

捕获长距离依赖: 任何两个词之间都可以直接计算相关性，彻底解决了RNN的序列距离问题。

生成上下文相关的动态表示: 一个词的最终表示不再是固定的，而是根据它所在的句子动态生成的。这是解决一词多义等问题的关键。

赋予模型可解释性: 通过可视化注意力权重，我们可以直观地看到模型在做决策时，重点关注了哪些输入部分，这为我们理解模型行为提供了窗口。

为什么需要用 Q, K, V 三个完全独立的参数矩阵？

简单来说，核心目的是：解耦和增强模型的表达能力，让输入序列中的每个元素（Token）能够扮演不同的角色。这三个矩阵将同一段输入映射到了三个不同的文本向量空间中，因为在注意力机制中，同一段文本作为 Query，key 和 Value 的含义是不同的，自然需要不同的向量空间去划分。

下面我们来详细拆解这个答案。

1. 核心思想：赋予输入信息不同的“角色”

W_Q：将输入向量投影到 “查询空间”。它的任务是刻画当前位置（如一个词）的“意图”或“需求”。例如，句子中的动词“吃”可能会产生一个寻找“食物”相关信息的Query。
W_K：将输入向量投影到 “键空间”。它的任务是刻画每个位置（如一个词）的“身份”或“特征”，用于被Query匹配。例如，“苹果”这个词作为Key时，可能会突出其作为“水果”的特征。
W_V：将输入向量投影到 “值空间”。它的任务是刻画每个位置所包含的“信息”或“内容”，这是最终被聚合的实际数据。例如，“苹果”这个词作为Value时，可能包含其词义、语法角色等更丰富的信息。
为什么需要不同的空间？ 因为一个词的“身份特征”（Key）和它所要提供的“信息内容”（Value）可能侧重点不同。同样，它的“需求”（Query）也和它的“身份”（Key）不同。独立的投影使得模型可以分别学习和优化这三种不同的表示，极大地增强了模型的容量和灵活性。

想象一下你在图书馆查资料的场景：

你脑子里想的问题是 查询（Query）。
为了找到相关的书，你会去看书架上每本书的 索引或标签（Key）。
当你找到一本书，你真正要阅读的是书本的 内容（Value）。

在自注意力（Self-Attention）机制中，输入序列里的每个词（Token）都需要同时扮演这三种角色： 1. 作为查询者（Query）：它要去“询问”序列中其他所有词，哪些词和“我”最相关。 2. 作为被查询者（Key）：它要“告诉”序列中其他所有词，“我”这里有什么样的信息可供匹配。 3. 作为内容贡献者（Value）：它包含了这个词本身所携带的真正信息。如果别的词注意到“我”，我就把这些信息传递过去。

如果 Q, K, V 是完全相同的（即都使用原始的词嵌入向量 $x$），那么一个词“查询”和“被查询”的表示就是完全一样的。这极大地限制了模型的灵活性。

通过引入三个独立的、可学习的权重矩阵 $W^Q, W^K, W^V$，我们可以将原始的输入嵌入向量 $X$ 投影到三个不同的子空间中，从而得到 $Q, K, V$ 矩阵：

\[
Q = XW^Q
\]

\[
K = XW^K
\]

\[
V = XW^V
\]

这里的 $X$ 是输入序列的嵌入矩阵，每一行代表一个词的嵌入向量。$W^Q, W^K, W^V$ 就是我们在训练过程中要学习的参数。

4. 分开的目的和带来的好处

将 Q, K, V 分开，主要有以下两大好处：

A. 极大地增强了模型的表达能力和灵活性

这体现在两个方面：

不同的相似度计算方式：注意力得分（Attention Score）是通过 Query 和 Key 的点积来计算的（$\text{score} = Q \cdot K^T$）。如果 $Q=K$，那么相似度计算就变成了向量和自身的点积，衡量的更多是“能量”大小，而不是两个不同视角下的“相关性”。
- 举个例子：在句子 "The animal didn't cross the street because it was too tired" 中，我们希望代词 it 能注意到 animal。
- it 作为 Query，它的任务是“我要找我指代的是谁”。
- animal 作为 Key，它的任务是“我是一个名词，可以被指代”。
- the 作为 Key，它的任务可能是“我是一个冠词，限定后面的名词”。
- 通过独立的 $W^Q$ 和 $W^K$ 矩阵，模型可以学习到让 it 的 $q$ 向量和 animal 的 $k$ 向量在语义上非常接近，从而产生高的注意力分数，而与其他词（如 the, street）的 $k$ 向量相距较远。如果 Q 和 K 表示相同，这种灵活的、非对称的匹配关系就很难学习到。
解耦了“寻找谁”和“提供什么”：
- Q-K 的交互决定了注意力权重：即 “应该关注谁，关注多少”。这相当于一个路由或寻址的过程。
- V 决定了聚合的信息内容：即 “从被关注的对象那里，应该获取什么信息”。
- 将 K 和 V 分开至关重要。一个词可能因为某个特征（Key）被注意到，但我们希望从中提取的信息（Value）却是另一个维度的。
- 继续上面的例子：it 注意到了 animal（通过 Q-K 匹配）。现在 it 需要从 animal 那里获取信息来更新自身的表示。animal 的 $v$ 向量可能就包含了“这是一只动物”的丰富语义信息，而不是它作为“被指代对象”的语法功能信息。模型通过 V 将 animal 的语义内容传递给 it，使得 it 的新表示中融合了 animal 的含义。如果 K=V，那么模型用来判断相关性的信息和最终要提取的信息就被绑定在了一起，不够灵活。

3. 数学公式回顾

让我们回顾一下 Scaled Dot-Product Attention 的完整公式，来巩固这个理解：

\[
\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V
\]

这个公式的计算过程清晰地体现了 Q, K, V 的不同作用： 3. 计算得分：$QK^T$ 计算每个 Query 对所有 Key 的注意力得分。 4. 缩放：除以 $\sqrt{d_k}$ （$d_k$是 Key 向量的维度）是为了在训练时获得更稳定的梯度。 5. 归一化：softmax 操作将得分转换成一个概率分布，所有 Key 的权重之和为 1。 6. 加权求和：将得到的权重应用到 Value 矩阵上，对所有的 $v$ 向量进行加权求和，得到最终的输出。

当面试官问到这个问题时，你可以这样组织你的回答：

先给结论：使用三个独立的矩阵 Q, K, V 是为了增加模型的表达能力和灵活性，让同一个输入词能在注意力计算中扮演三个不同的角色：查询者（Query）、被查询者（Key）和内容贡献者（Value）。
解释角色：用一个通俗易懂的例子（如图书馆查资料）来解释 Q, K, V 的含义。
阐述分离的好处 (核心)：
- 表达灵活性：$W^Q$ 和 $W^K$ 将输入投影到不同的空间，使得模型可以学习非对称的相关性。比如代词 it (Query) 和它指代的名词 animal (Key) 之间的关系。
- 解耦：最关键的一点是解耦。Q-K 的交互决定了注意力权重（关注谁），而 V 决定了要提取的信息内容（拿什么）。这种解耦让模型可以因为 A 原因关注某个词，但提取 B 内容，这是非常强大的能力。
(加分项) 如果不分开会怎样：简单提一下，如果 Q=K=V，模型就只能计算原始嵌入向量之间的相似度，并聚合这些原始向量，这大大限制了模型捕捉复杂上下文依赖关系的能力。

为什么需要多个头？

简单来说，多头注意力（Multi-Head Attention）机制允许模型在不同的表示子空间中，从不同的角度同时关注信息。 这极大地增强了注意力层的建模能力。

Gemini 提供的一个生动的比喻：

单头 vs. 多头：一个专家 vs. 专家委员会

单头注意力（Single-Head Attention）：就像你只请了一位语法专家来阅读一个句子。当他读到 "The animal didn't cross the street because it was too tired" 时，他可能会根据语法规则，非常准确地将 it 和 animal 联系起来（主语和代词的指代关系）。但他可能不会特别关注 tired 和 animal 之间的描述关系。他的注意力模式是单一的，被他唯一的专业视角所主导。
多头注意力（Multi-Head Attention）：这相当于你组织了一个专家委员会。
- Head 1 (语法专家)：专注于 it -> animal 的指代关系。
- Head 2 (语义专家)：专注于 tired -> animal 的状态描述关系。
- Head 3 (上下文专家)：可能会关注 street 和 cross 之间的动作-地点关系。
- Head 4 (否定关系专家)：可能会关注 didn't 对整个句子语义的翻转。
- ...等等。

每个“头”都是一个独立的专家，有自己的一套 Q, K, V 权重矩阵。它们并行工作，各自从不同的“表示子空间”中提取信息，并形成自己的注意力结论。

🤔：为什么单头不够好？

单头注意力的主要局限性在于 “平均化效应”。

因为它只有一套 $W^Q, W^K, W^V$ 矩阵，它必须学习一种“万金油”式的注意力模式，试图同时兼顾语法、语义、指代等所有可能的关系。这会导致它的注意力可能不够“专注”和“尖锐”。模型可能会学习到一种将所有类型的相关性都混合在一起的平均表示，而不是针对特定关系形成清晰的连接。这限制了模型捕捉句子中多样化、多维度特征的能力。

🤔 多头如何工作？以及拼接的目的？

多头注意力的工作流程非常清晰，这也解释了为什么需要最后一步的拼接和线性变换。

假设我们有 $h$ 个头（例如，在 Transformer Base 模型中 $h=8$），模型的维度是 $d_{model}$（例如 512）。每个头有独立的参数。

- 首先，模型为每个头 $i$（从 1 到 $h$）创建三组独立的权重矩阵：$W^Q_i, W^K_i, W^V_i$。
- 然后，将原始的输入嵌入 $X$ 分别通过这些权重矩阵，为每个头生成各自的 $Q_i, K_i, V_i$。
- 通常，我们会把原始的 $d_{model}$ 维度切分开。每个头的 Q, K, V 向量维度会是 $d_k = d_v = d_{model} / h$。例如，512 维的输入，分成 8 个头，每个头就在一个 64 维的子空间里进行计算。
投影/分裂（Projection/Splitting）：
```
\[
Q_i = XW^Q_i, \quad K_i = XW^K_i, \quad V_i = XW^V_i
\]
```
并行计算注意力（Parallel Attention Calculation）：
- 每个头都独立地、并行地执行标准的 Scaled Dot-Product Attention 计算，得到各自的输出 head_i。
```
\[
\text{head}_i = \text{Attention}(Q_i, K_i, V_i) = \text{softmax}(\frac{Q_i K_i^T}{\sqrt{d_k}})V_i
\]
```
这一步就是“专家委员会”里每个专家独立工作，产出各自的分析报告。
拼接与线性变换（Concatenation & Final Linear Projection）：
- 拼接(Concatenation)：将所有 $h$ 个头的输出 head_i 在维度上拼接起来。
```
\[
\text{Concat}(\text{head}_1, \text{head}_2, ..., \text{head}_h)
\]
```
  拼接后的矩阵维度又恢复到了 $d_{model}$ ($h \times d_v = h \times (d_{model}/h) = d_{model}$)。此时，我们得到的是一个包含了所有专家独立意见的“汇总文件包”。
- 最终线性变换（Final Linear Projection）：这是你问题的关键！ 仅仅拼接是不够的，因为那只是把各个子空间的结果简单地并排放在一起。我们需要一个机制来整合和融合这些来自不同子空间的信息。
  - 模型引入了一个额外的、可学习的权重矩阵 $W^O$（输出权重矩阵）。
  - 将拼接后的矩阵乘以这个 $W^O$，得到多头注意力的最终输出。
```
\[
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O
\]
```
  这个 $W^O$ 矩阵的作用就像是“委员会主席”。它查看所有专家（头）的报告，并学习如何将它们智能地组合起来。它会决定在当前的上下文中，哪个专家的意见更重要，哪个次要，以及如何将这些不同的意见（特征）融合成一个统一、连贯、信息更丰富的最终表示。

核心目的：多头注意力机制的核心目的是让模型能够从不同的表示子空间、从不同的角度去关注信息，从而更全面地捕捉数据中的多样化特征。
单头的局限：单头注意力容易产生“平均效应”，难以同时学习多种不同类型的依赖关系。
多头的工作方式：通过为每个头设置独立的 $W^Q, W^K, W^V$ 矩阵，将原始表示投影到多个子空间中，并行计算注意力。
拼接与最终投影的目的：拼接是把各个头独立计算的结果收集起来。而最后的线性投影层（$W^O$）是至关重要的，它负责融合所有头的信息，学习如何智能地组合这些从不同角度提取的特征，生成一个统一且更丰富的输出表示。它不是简单的相加，而是一种可学习的、加权的组合。

Softmax: usage⚓︎

Softmax 确保注意力分数转换为有效的概率分布，所有值都在 0 到 1 之间，总和等于 1。此属性对于正确权衡输入标记，同时考虑其相对重要性非常重要。

总之，softmax 函数是 Transformer 的重要组成部分，它使它们能够学习如何根据输入标记与当前上下文的相关性来加权输入标记，从而使模型的自注意力机制有效地捕获数据中的依赖关系和关系

Cross / Self-Attention⚓︎

问题1：为什么一定要用交叉注意力？它的作用是什么？

在经典的 Encoder-Decoder Transformer 架构（例如用于机器翻译、文本摘要的模型）中，交叉注意力（Cross-Attention）是不可或缺的，它的核心作用是充当编码器（Encoder）和解码器（Decoder）之间的桥梁，实现两个不同序列之间的信息对齐和传递。

让我们把它放在具体的场景里来理解：

假设我们在做一个中译英的任务：“我是一个学生” -> "I am a student"。

编码器（Encoder）的工作：
- Encoder 接收中文输入序列 "我", "是", "一个", "学生"。
- 通过其内部的自注意力（Self-Attention）层，它会充分理解这个中文句子内部的依赖关系，并为每个词生成一个富含上下文信息的表示（representation）。
- Encoder 的最终输出是一个包含了整个源句子信息的向量序列，我们称之为 $H_{enc}$。这个 $H_{enc}$ 就相当于对整个中文句子的“深度理解”或“知识库”。
解码器（Decoder）的工作：
- Decoder 的任务是逐词生成英文目标序列。比如，当它已经生成了 "I", "am" 之后，它需要决定下一个词是什么。
- 此时，Decoder 需要参考两个方面的信息：
  - 已经生成的部分：它需要看看自己已经写了 "I am"，这通过 Decoder 内部的带掩码的自注意力（Masked Self-Attention）来实现。
  - 原始的中文句子：它必须回头看中文原文，才能知道接下来该翻译哪个部分。这就是交叉注意力发挥作用的地方！

Mechanism of Cross Attention⚓︎

在 Decoder 的交叉注意力层： * Query (Q): 来自于 Decoder 的前一个输出。它代表了 Decoder 当前的状态，相当于在提问：“根据我已经生成的 'I am'，接下来我最应该关注原文中的哪个部分来生成下一个词？” * Key (K) 和 Value (V): 来自于 Encoder 的最终输出 ($H_{enc}$)。它们代表了源句子（中文）的完整信息库。Key 用于和 Query 匹配，Value 包含了要提取的实际信息。

\[
\text{CrossAttention}(Q_{dec}, K_{enc}, V_{enc}) = \text{softmax}(\frac{Q_{dec}K_{enc}^T}{\sqrt{d_k}})V_{enc}
\]

所以，交叉注意力的整个过程就是：Decoder 在生成每一个词的时候，都会用自己的当前状态（Q）去“查询”一遍 Encoder 提供的完整上下文（K 和 V），然后有选择性地、动态地“聚焦”在源句子中最相关的部分，并将这些信息提取出来用于生成下一个词。

比如在生成 a 的时候，交叉注意力可能会让模型高度关注中文的 一个；在生成 student 的时候，高度关注 学生。

Transformer 中，这三个矩阵为什么不能被取代？

在 Encoder-Decoder 架构中，这个信息桥梁的功能是必须的。在 Transformer 出现之前，RNN/LSTM 类的 Seq2Seq 模型试图用一个固定长度的向量（context vector）来压缩整个源句子的信息，这就是一个巨大的信息瓶颈。无论源句子多长、多复杂，都必须被压缩成同一个大小的向量，这必然会导致信息丢失。

交叉注意力机制通过允许 Decoder 在每一步都直接访问 Encoder 的所有输出，彻底解决了这个瓶颈问题。因此，可以说在这种架构范式下，交叉注意力是目前最优且核心的解决方案，很难被其他机制以同等效率和效果取代。

问题2：Decoder-Only 架构与交叉注意力的关系

这个问题的追问是，现在更多的大模型是 Decoder- Only架构的了，那么他们是不是就很少用到交叉注意力机制，而单纯地是在原先自注意力机制上进行调整优化，比如Flash Attention，Linear Attention，Sparse Attention？

是的，像 GPT 系列、LLaMA、PaLM 这类主流的大语言模型（LLM）都是 Decoder-Only 架构，它们在其核心的预训练和生成任务中，确实不使用交叉注意力机制。

NO Cross Attention for Decoder-Only!⚓︎

因为它们的工作模式和任务定义与 Encoder-Decoder 模型完全不同。

Encoder-Decoder 模型：处理的是 输入序列 A -> 输出序列 B 的任务，比如翻译（中文 -> 英文）、摘要（长文章 -> 短摘要）。这里有两个明确区分的序列，所以需要一个机制（交叉注意力）来连接它们。
Decoder-Only 模型：处理的是 prompt -> completion 的任务。从模型的角度看，这并不是两个独立的序列。prompt（提示）和 completion（补全）被拼接成一个单一的、连续的序列。模型的唯一任务就是根据前面的所有 token，预测下一个 token。

例如，当你给 GPT 输入 中国的首都是，并让它补全时，对于模型来说，它的输入序列就是 ["中国", "的", "首都", "是"]。它的任务是预测第五个 token，它会通过自注意力（Self-Attention）机制来关注前面这四个 token，然后生成 北。接着，序列变成 ["中国", "的", "首都", "是", "北"]，模型再根据这五个 token 预测下一个 京。

在这个过程中，始终只有一个序列在不断增长，模型也只关注这个序列自身内部的关系，所以只需要自注意力就足够了。

Decoder Only 架构模型优化重点的转移

由于 Decoder-Only 模型完全依赖于自注意力，并且处理的序列长度（Context Window）越来越长（从 2k 到 4k，再到 32k，甚至 1M+），自注意力机制的平方复杂度（$O(N^2)$，其中 $N$ 是序列长度）成为了最主要的性能瓶颈。

因此，学术界和工业界的研究重点自然就转向了如何优化自注意力机制本身。你提到的几个例子都非常典型：

FlashAttention：这是一个里程碑式的工作。它本身没有改变注意力的数学计算，而是一种 I/O 感知的算法，通过优化 GPU 内存（SRAM 和 HBM）之间的数据读写，避免了反复读取完整的 $N \times N$ 注意力矩阵，从而在不牺牲精度的情况下，极大地提升了计算速度并减少了内存占用。这是目前长序列训练和推理的标配。
Linear Attention / Sparse Attention：这些是近似注意力的方法。它们试图通过修改注意力的计算方式来降低复杂度。
- Sparse Attention：认为不是每个 token都需要关注所有其他 token，因此只计算部分重要的 Q-K 对的得分，比如只关注相邻的或者一些全局的 token。
- Linear Attention：通过数学变换（如核函数）将 $softmax(QK^T)V$ 的计算顺序改变，使其复杂度降低到线性级别 $O(N)$。

一个重要的例外：虽然纯文本的 Decoder-Only 模型不用交叉注意力，但在多模态（Multi-modal）领域，交叉注意力又重新焕发了生机！例如，对于一个看图说话的模型（输入图片，输出文字描述），模型可能会使用： * 一个 Vision Encoder（如 ViT）来处理图片，得到图片的特征表示。 * 一个 Text Decoder（类似 GPT）来生成文字。 * 在 Text Decoder 中，会加入交叉注意力层，让文本在生成时能够“看”到（attend to）图片编码器的输出特征。这和经典的 Encoder-Decoder 架构在思想上是一脉相承的。

Masked Self Attention⚓︎

核心原因有两个：模拟真实生成过程和防止数据泄露。

在像机器翻译、文本生成这样的任务中，Decoder 的作用是自回归 (Auto-regressive) 地一个词一个词地生成目标序列。

我们来想象一个翻译任务的场景：将 "I am a student" 翻译成 "我是一个学生"。

训练阶段 (Training): 在训练时，我们为了高效，会把完整的德语目标序列 "我是一个学生" (<eos>) 一次性喂给 Decoder。模型的任务是，在输入了 "我" 之后，能预测出 "是"；在输入了 "我是" 之后，能预测出 "一个"，以此类推。

现在问题来了：如果没有 Mask，当模型在预测第3个位置的词 "一个" 时，它的 Self-Attention 机制能够看到完整的输入序列，包括它应该预测的 "一个" 和后面的 "学生"。

这就相当于开卷考试，模型可以直接"抄袭"后面的答案，而没有真正学会根据上文来预测下一个词的能力。这就是数据泄露 (Data Leakage)。它会让模型在训练集上表现得很好（因为总能抄到答案），但在实际需要自己一个词一个词生成的测试阶段，表现会非常差。
推理阶段 (Inference): 在实际生成时，模型是不知道未来信息的。它生成了 "我"，然后将 "我" 作为输入，预测出 "是"；再将 "我是" 作为输入，预测出 "一个"... 这个过程是严格遵守时间顺序的。

为了让训练阶段的行为模式和推理阶段保持一致，我们必须在训练时引入一个机制，强制模型在预测当前位置 i 的时候，只能关注到位置 i 以及它之前的所有位置 0, 1, ..., i-1，而不能看到任何未来的信息 i+1, i+2, ...。

这个机制，就是 "Sequence Mask" 或者叫 "Causal Mask"。

总结一下：

目的：确保模型在预测当前词时，只依赖于已经生成的词（过去和现在的信息），而不会依赖于未来的词（作弊信息）。
本质：强制 Self-Attention 变成一种单向的、有因果顺序的注意力机制，这与 Encoder 中可以自由查看所有上下文的双向注意力形成对比。

具体而言， Mask 是作用在计算出 Attention 分数之后，但在进行 Softmax 操作之前。

我们回顾一下 Self-Attention 的核心计算公式：

\[
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V
\]

Masking 的关键步骤就发生在 softmax 函数的内部。具体来说：

计算 Attention Score: 首先，我们正常计算 Query 和 Key 的点积来得到注意力分数矩阵 scores。假设我们的序列长度为 seq_len，那么多头注意力中每个头的 scores 矩阵维度就是 (seq_len, seq_len)。

$S = QK^T$
创建 Mask 矩阵: 我们创建一个与 scores 矩阵同样大小的 Mask 矩阵。这个矩阵的上三角部分（不含对角线）是 True 或者 1，其余部分是 False 或者 0。这个矩阵直观地表示了哪些位置是“未来”，需要被遮住。例如，对于一个长度为4的序列，Mask 矩阵（布尔形式）看起来像这样：
```
[[False, True,  True,  True],
 [False, False, True,  True],
 [False, False, False, True],
 [False, False, False, False]]
```
True 代表需要被 Mask 掉的位置。
应用 Mask: 接下来是最关键的一步。我们会把 scores 矩阵中，凡是 Mask 矩阵中为 True 的位置，都替换成一个非常小的负数 (比如 -1e9 或者负无穷 -inf)。

为什么要用一个极小的负数，而不是直接设为0呢？

因为下一步就是 Softmax。Softmax 的计算是 $e^x$。如果我们将一个位置的值设为负无穷，那么 $e^{-\infty} \approx 0$。这样一来，经过 Softmax 归一化后，这些被 Mask 掉的位置的注意力权重就变成了零，相当于在计算后续的加权和时，完全忽略了这些位置的 Value。

如果只是设为0，那么 $e^0 = 1$，它依然会在 Softmax 中占有一定的权重，这就无法达到“遮蔽”的效果了。

How to prevent Gradient Loss? (🤔)⚓︎

这触及了深度学习模型能够“网络越堆越深”的根本原因。

以下三大法宝来克服梯度消失：

残差连接 (Residual Connections) -> 来自 ResNet
层归一化 (Layer Normalization) -> 来自 Transformer
ReLU (及其变体) 激活函数

下面我们逐一拆解。

残差连接 (Residual Connections / Skip Connections)

这是解决梯度消失问题的最核心的武器，是 BERT 乃至整个 Transformer 架构能够堆深的基石。

问题是什么？

在非常深的网络中，梯度需要从最后一层反向传播到第一层。在链式法则的作用下，梯度会经过一系列矩阵乘法。如果许多梯度值都小于1，那么连乘之后梯度会迅速缩小，趋近于0，这就是梯度消失。这导致底层的网络层几乎无法得到更新，学不到东西。

残差连接如何解决？

BERT的每一个子层（无论是多头注意力还是前馈网络）都采用了残差连接。其结构是：

\[ H(x) = F(x) + x \]

$x$ 是子层的输入。
$F(x)$ 是子层的映射函数（如 Self-Attention 或 FFN 的计算）。
$H(x)$ 是子层的最终输出。

这个简单的 + x 操作，创造了一条“高速公路”。在反向传播时，损失函数对 $x$ 的梯度 $\frac{\partial \text{Loss}}{\partial x}$ 会变成：

\[
\frac{\partial \text{Loss}}{\partial x} = \frac{\partial \text{Loss}}{\partial H} \cdot \frac{\partial H}{\partial x} = \frac{\partial \text{Loss}}{\partial H} \cdot \left( \frac{\partial F(x)}{\partial x} + 1 \right)
\]

因为那个 +1 的存在，梯度在反向传播时就有了一个直接向后传递的恒等路径。即使 $\frac{\partial F(x)}{\partial x}$ 很小趋近于0，梯度也能保证至少以接近1的比例回传。这极大地缓解了梯度消失问题，保证了即使在非常深的网络中，底层的网络层也能接收到有效的梯度信号。

Transformer Encoder 中，每个 Add & Norm 中的 Add 就是在执行残差连接。

层归一化 (Layer Normalization)

如果说残差连接是“开源”，那么层归一化就是“节流”。它通过稳定数据分布，让梯度传播更顺畅。

问题是什么？ 在深层网络中，每一层的参数更新都会导致其输出数据的分布发生变化。对于下一层来说，它的输入分布一直在变来变去，这种现象叫做内部协变量偏移 (Internal Covariate Shift)。这使得模型训练变得不稳定，就像在流沙上盖楼一样。不稳定的数据分布也可能导致梯度变得过大（爆炸）或过小（消失）。

LayerNorm 如何解决？ Layer Normalization 在每一层的输入端，对数据进行归一化处理。具体来说，它会计算单个样本在特征维度上的均值和方差，然后将该样本的激活值标准化为均值为0，方差为1的分布。

这个操作有两大好处：

稳定数据分布：无论前一层的参数如何变化，经过 LayerNorm 之后，输入到下一层的数据分布都会被“拉回”到一个相对固定的、稳定的状态。这使得训练过程更加稳定。
维持梯度尺度：通过将数据缩放到一个固定的范围内，可以有效防止激活值过大或过小，从而避免了梯度因为激活值本身的大小问题而发生爆炸或消失。它让梯度在网络中传播时保持在一个“健康”的范围内。

在 BERT 的 Add & Norm 中的 Norm 就是在执行层归一化。它通常被放在残差连接之后，对 F(x) + x 的结果进行归一化，然后再送入下一层。

ReLU 激活函数

这是一个看似简单但非常有效的选择。

问题是什么？

像 Sigmoid 或 tanh 这样的激活函数，它们的导数在大部分区域都小于1，特别是在函数饱和区（输入值很大或很小时），导数几乎为0。在反向传播中，梯度会乘以这些小于1的导数，导致梯度快速衰减。

ReLU 如何解决？

BERT 的前馈网络（Feed-Forward Network, FFN）部分通常使用 ReLU 的变体，如 GELU (Gaussian Error Linear Unit)。但我们可以先用简单的 ReLU 来理解其优势。

ReLU 函数 $f(x) = \max(0, x)$ 的特点是： * 当输入 $x > 0$ 时，其导数为 恒等于 1。 * 当输入 $x \le 0$ 时，其导数为 0。

这个“导数为1”的特性意味着，对于被激活的神经元，梯度在反向传播经过它时不会有任何衰减，可以原封不动地向后传递。这在很大程度上缓解了梯度消失问题。GELU 具有和 ReLU 类似的优点，同时在负值区有更平滑的导数，实践中效果更好。

比如在 Bert 中：

解决策略	具体技术	在BERT中的位置	作用机理
创建梯度高速路	残差连接 (Residual Connection)	每个子层的 `Add & Norm` 块	保证梯度至少有条恒等路径可以回传，避免因连乘而消失。
稳定梯度环境	层归一化 (Layer Normalization)	每个子层的 `Add & Norm` 块	稳定每层输入的数据分布，让梯度尺度保持在“健康”范围。
避免梯度衰减	ReLU / GELU 激活函数	前馈网络 (FFN)	在激活区，其导数恒为1（或接近1），不会让梯度在传播中衰减。

正是这套从 ResNet 和 Transformer 继承而来的成熟设计，使得 BERT 可以放心地将模型做得非常深，从而获得强大的语言表示能力。

Adam Optmz: Features (🤔)⚓︎

一句话概括：

Adam 优化器可以被看作是一个更智能、更高效的“梯度下降”方法。它的主要作用是指导模型在训练过程中如何有效地更新参数（权重），从而更快、更稳定地找到损失函数的最小值。

一个经典的类比：

想象一下，你站在一座连绵不绝的山脉上，眼睛被蒙住，你的任务是尽快走到山脉的最低点（也就是损失函数的最小值点）。

普通梯度下降 (SGD)：你每走一步，都会伸脚试探一下当前位置最陡峭的方向，然后朝那个方向迈出一小步。但如果这个山谷是一个狭长而弯曲的峡谷，你可能会在峡谷两侧来回震荡，走得很慢。
Adam 优化器：你就像一个拥有“惯性”和“环境感知能力”的智能小球。
- 惯性：你不会每一步都完全改变方向，而是会保留一部分上一步的速度，让你能冲过平坦的区域，并抑制在峡谷两侧的震荡。
- 环境感知：你会根据脚下路面的“崎岖程度”来动态调整步伐。在平坦的大路上（梯度小的参数），你会迈出更大的步子；在崎岖不平的陡坡上（梯度大的参数），你会小心翼翼地迈出小步子，防止冲过头。

Adam 这个名字来源于 Adaptive Moment Estimation（自适应矩估计），它巧妙地结合了两种强大的优化技术：

1. 动量 (Momentum) - 决定“方向”的惯性
作用: 解决普通梯度下降在某些地形（如狭长山谷）中收敛慢、易震荡的问题。
原理: 它引入了“一阶矩估计”，可以理解为梯度的指数移动平均值。简单来说，它不仅考虑当前这一步的梯度方向，还参考了之前几步的平均方向。
- 当梯度方向一致时，这个“动量”会累积，使得更新步伐加速。
- 当梯度方向来回摆动时，这个“动量”会相互抵消，起到抑制震荡的作用。
1. 自适应学习率 (RMSprop) - 决定“步长”的感知能力
作用: 解决所有参数都共享同一个学习率（步长）的低效问题。
原理: 它引入了“二阶矩估计”，可以理解为梯度平方的指数移动平均值。这个值可以衡量一个参数梯度的“历史波动性”或“大小”。
- 对于历史上梯度一直较小的参数（路面平坦），Adam 会用一个较小的分母来除，使得有效学习率变大，从而迈出更大的步子。
- 对于历史上梯度一直较大的参数（路面陡峭），Adam 会用一个较大的分母来除，使得有效学习率变小，从而迈出更小的步子，防止“冲出”最优解。

总结起来，在每一步更新时： Adam = 用“动量”算出一个大致的前进方向 + 用“自适应学习率”机制决定每个参数在该方向上该走多远。

补充一点，Adam 还包含一个偏差修正（Bias Correction）步骤，用于修正在训练初期，移动平均值会偏向于零的问题，确保初始阶段的步长不会过小。

为什么它成为了默认首选？
收敛速度快：结合了动量和自适应学习率的优点，在大多数情况下比其他优化器收敛得更快。
实现简单，效果稳健：在各种模型和数据集上都表现良好，是“开箱即用”的可靠选择。
对超参数不那么敏感：它的几个关键超参数（如 beta1, beta2, epsilon）通常使用默认值就能取得不错的效果，减少了调参的负担。

面试精炼版回答⚓︎

面试官您好，关于Adam优化器，我的理解是：

它的作用：Adam是一种高效的梯度下降优化算法，用来在模型训练时指导参数更新，目标是更快、更稳定地找到损失函数的最小值。
核心思想：它结合了两种经典优化思想。一是“动量（Momentum）”，通过计算梯度的指数移动平均（一阶矩），为参数更新引入“惯性”，以加速收敛并抑制震荡。二是“自适应学习率（Adaptive Learning Rate）”，通过计算梯度平方的指数移动平均（二阶矩），为模型中的每一个参数动态地、独立地计算学习率，使得在梯度平缓的参数上步长大，在梯度陡峭的参数上步长小。
为什么流行：Adam综合了上述优点，收敛速度快，在各种任务中表现稳健，而且超参数相对不敏感，使其成为了绝大多数深度学习任务的默认首选优化器。

How to prevent Overfitting?⚓︎

过拟合 (Overfitting) 的本质是模型学到了训练数据中的“噪声”和“偶然规律”，而没有学到普适的、可泛化的“通用规律”。其表现为：模型在训练集上表现极好，但在从未见过的验证集或测试集上表现很差。

对于动辄拥有数十亿甚至上万亿参数的大模型来说，其“记忆”能力极强，因此防止过拟合尤为关键。下面是从不同维度梳理的常用方法：

数据增强 (Data Augmentation)

核心思想: 当数据量有限时，通过各种技术创造出新的、合理的训练数据。 * 应用: * 传统方法: 例如回译 (Back-translation)（如 中文 -> 英文 -> 新的中文），或在句子中进行同义词替换。 * 现代方法: 使用另一个强大的 LLM 来生成高质量的训练数据，比如对一条指令进行多样化的改写，或者生成更多样的回答。

数据清洗 (Data Cleaning)

核心思想: 确保训练数据的质量。如果数据本身包含大量错误标签或噪声，模型会努力去“拟合”这些错误，这本身就是一种过拟合。应用: 去除或修正训练集中标注错误的样本、格式混乱的数据等。

参数高效微调 (PEFT, e.g., LoRA)

核心思想: 这是大模型时代最重要的正则化手段之一。通过冻结绝大部分预训练参数，只训练一小部分新增的、低秩的“适配器”参数 (如 LoRA 中的 A, B 矩阵)，极大地限制了模型可以改变的自由度。 * 应用: 在 SFT 或特定领域微调时，使用 LoRA 技术。模型无法轻易撼动其庞大的预训练知识库去死记硬背新的小数据集，只能在原有能力的基础上进行微调，天然地防止了灾难性遗忘和过拟合。

Dropout

核心思想: 在训练过程中的每一次前向传播时，随机地将一部分神经元的输出设置为零。

应用: BERT 和其他 Transformer 模型中的全连接层和注意力层后都应用了 Dropout。这强迫网络不能过度依赖任何单一的神经元，必须学习更加鲁棒和分散的特征表示，就像一个团队里随机让几个人“轮休”，强迫其他人学会合作和备份。

权重衰减 (Weight Decay / L2 Regularization)

核心思想: 在损失函数中增加一个惩罚项，该项与模型权重的平方和成正比 ($L = L_{\text{original}} + \lambda \sum w^2$)。这会“惩罚”过大的权重。 * 应用: 这是几乎所有深度学习训练中的标配。它鼓励模型学习到更小、更分散的权重，使得模型的输出对输入中微小的、噪声性的变动不那么敏感，从而提高了泛化能力。

早停 (Early Stopping)

核心思想: 在训练过程中，除了计算在训练集上的损失，同时还要在一个独立的验证集 (Validation Set) 上监控模型的性能（如准确率、困惑度）。当模型在训练集上的损失仍在下降，但在验证集上的性能开始变差时，就立即停止训练。 * 应用: 非常实用且广泛应用的策略。它直接抓住了过拟合的定义（验证性能下降），在模型“走火入魔”之前及时叫停。

标签平滑 (Label Smoothing)

核心思想: 在分类任务中，将硬性的 one-hot 标签（如 [0, 0, 1]）软化成一个平滑的分布（如 [0.05, 0.05, 0.9]）。 * 应用: 这相当于告诉模型：“不要对你的判断过于自信，这个样本虽然是C类，但它也可能有A类和B类的一点点特征”。这可以防止模型为了在某个样本上达到100%的置信度而产生非常大的 logits，使得模型决策边界更平滑，泛化性更好。

总结对比⚓︎

方法类别	具体方法	核心思想	典型应用场景
数据层面	增加数据量	让模型见多识广，难以死记硬背	所有阶段，尤其是资源允许的预训练
	数据增强	从现有数据中创造新的合理数据	微调数据量不足时
模型层面	LoRA (PEFT)	限制模型可训练参数量，约束其能力	大模型微调阶段最主流的正则化手段
	Dropout	随机让神经元“失活”，强迫网络学习鲁棒特征	Transformer 中的 FFN 和 Attention 层
训练层面	权重衰减 (L2)	惩罚过大的模型权重，使模型更平滑	几乎所有模型的优化器设置中
	早停 (Early Stopping)	在验证集性能下降时停止训练	几乎所有监督学习的训练流程中
	标签平滑	软化标签，防止模型对预测过于自信	分类任务的损失函数设计中

$\beta$