列生成算法 (Column Generation)⚓︎
约 5122 个字 6 张图片 预计阅读时间 17 分钟 总阅读量 次
参考链接
-
同济大学梁哲老师的这个视频,合集整理得十分详细,中英文课程都有,还有很多参考链接。
-
东南大学程琳老师课题组的讲解视频,侧重于从单纯形法到列生成的联系、启示、几何展示与一些数学推导;
-
代码编程:推荐Gurobi 官网的 CSP傻瓜教程。写得很专业,有官方提供的代码。页面能帮你把可视化结果都搞出来,寓教于乐。
从单纯形法开始⚓︎

左右两个线性规划问题,LP2只是增加了两个变量,单纯形表引入了两个新列,但是都是非基变量,加入两个列之后对最优解没有影响。

在实际中,可能存在一系列问题,他们的列很多,没有办法把这些列枚举穷尽完,而单纯形法在出入基操作上每次都需计算检验数,需要显式地对入基的列进行计算。
所以可以反过来考虑,让一个初始没有包含所有最优基的一个单纯形表慢慢生长,变成一个包含了最优基的表,通过求解这个单纯形表,在不用显式遍历所有列的情况下,能够更早地求得最优解。
三个思路
- 没有必要添加所有的变量。(No need for all variables)
- 开始时,只需要一个可行的基。(Initially, find feasible variables)
- 最终要生成一个最优基。(Optimal basis!)
假设我们枚举单纯形表所有的列,这个单纯形表对应的就是主问题(Master Problem, MP)。一开始,我们没有枚举所有的列,此时的单纯形表是不完整的,对主问题的描述也不完整,这张表对应的就是 受限主问题(Restricted Master Problem, RMP) 。 而,解决“找到一个列,加入到受限主问题中”这个过程的问题,就是子问题(Sub Problem)。
列生成,对基采用了隐枚举的方式,利用求解子问题,从受限主问题不断生成更好的基,直到出现最优基,此时受限主问题便等价于主问题,但是结构更加轻巧。
Cutting Stock Problem(下料问题)⚓︎
有三种型号的木材,9寸、14寸和16寸的木材,其成本分别为5,9,10. 我们也有一系列的订单:
| 原料长度 | 成本 | 小木材长度 | 需求数量 |
|---|---|---|---|
| 9 | 5 | 4 | 30 |
| 14 | 9 | 5 | 20 |
| 16 | 10 | 7 | 40 |
怎么切分这些木材(假设原料数量是够用的),使得所用到的木材的成本最小。
这个问题最初是前苏联科学家Kantorovich提出并建模的,最初的模型与现在略有不同,也更加复杂一点,先展开目前我们最常用的解决方法。
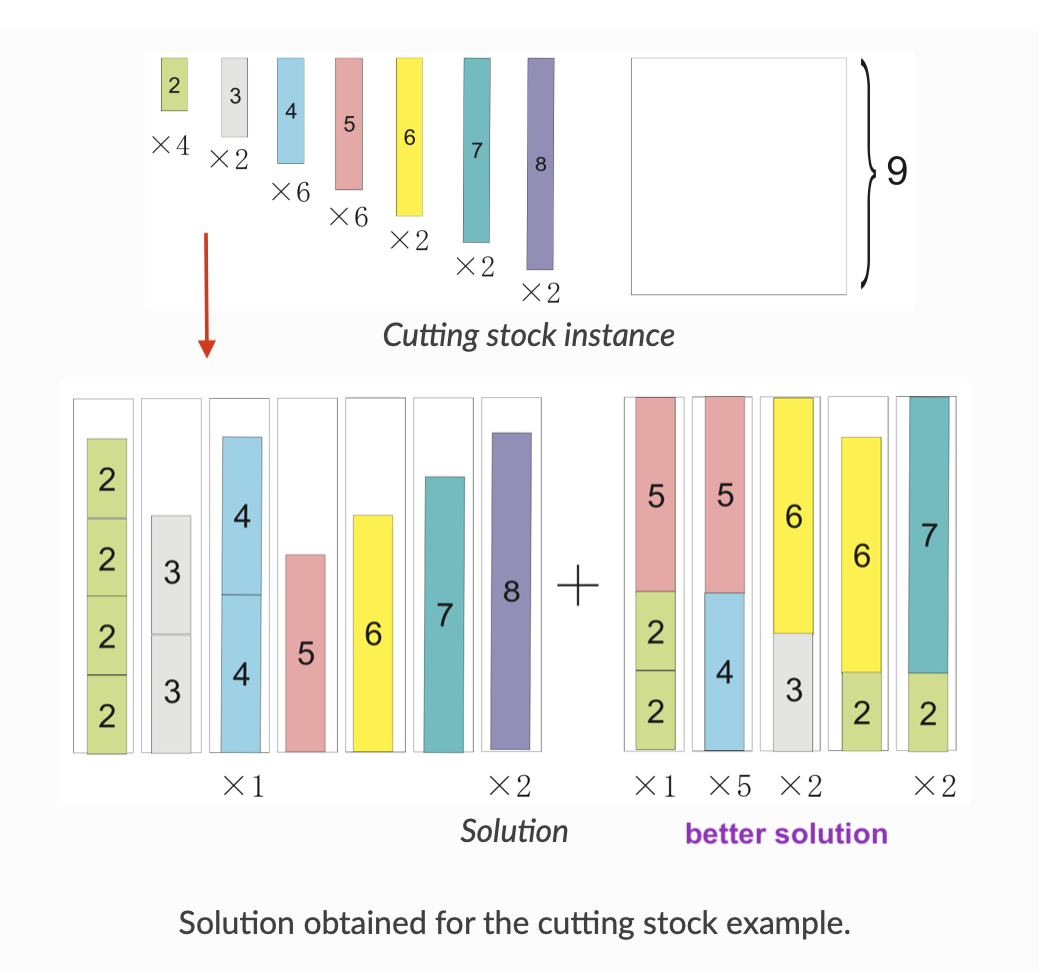
比如,对于原料木板,列出一些切割方法(Cutting Pattern)。什么是切割方法?比如,对于 一个 9寸的木板,我们可以这样切:
- 切成2个4寸的;剩下1寸废料;
- 它切成1个4寸的,一个5寸的;不剩废料;
对于一个14寸的木板,我们可以:
- 切成3个4寸的,剩下2寸废料;
- 切成2个4寸的,一个5寸的,剩下1寸废料;
- 切成2个4寸的,剩下6寸废料,这种情况下一眼就能看出来,效率不高,分明可以用1个9寸木板就切出来,不仅废料数量多,而且2个4寸的切法可以用一个9寸的切出来。
- ... etc
不过先不从浪费的角度考虑,上述每一种切法就构成了一个Pattern。我们简单罗列一下,就能发现很多很多个Pattern :
| 方案 | 切出的4寸个数 | 切出的5寸个数 | 切出7寸的个数 | 需要的成本(也就是单个原料的成本) |
|---|---|---|---|---|
| \(s_1\) | 2 | 0 | 0 | 5 |
| \(s_2\) | 1 | 1 | 0 | 5 |
| \(s_3\) | 0 | 0 | 1 | 5 |
| \(s_4\) | 3 | 0 | 0 | 9 |
| \(s_5\) | 2 | 1 | 0 | 9 |
| \(s_6\) | 1 | 2 | 0 | 9 |
| \(s_7\) | 1 | 0 | 1 | 9 |
| \(s_8\) | 0 | 1 | 1 | 9 |
| \(s_9\) | 0 | 0 | 2 | 9 |
| \(s_{10}\) | 4 | 0 | 0 | 10 |
| \(s_{11}\) | 2 | 0 | 1 | 10 |
| \(s_{12}\) | 1 | 1 | 1 | 10 |
| \(s_{13}\) | 0 | 3 | 0 | 10 |
| ... | ... | ... | ... | ... |
上面列的不是“所有可能的pattern”,仅作示意,实际切法很多,我们主要罗列的是“比较高效利用木板”的切法。
现在我们的目标就变成了“最小化总成本,也就是所用的切法的成本 \(\times\) 用这种切法的木板数”。
接下来写数学模型。
决策变量:\(x_j\) : 采用第 \(j\) 种切割方案切割的木材原料的数量。
参数:\(c_j\) : 与第 \(j\) 种切割方案相关的参数,指第 \(j\) 种切割方案切的原料的成本。比如第 \(j\) 种方案切的是3种原料木材里的第1种,那么这值就是1根第1种木料的成本,许多个切割方案会对应同一个成本。
\[\min \sum_j c_j x_j \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
\sum_j \mathbb{a_j} \mathbb{x_j} \geq \mathbb{b} \\
x_j \in \mathbf{Z}
\end{cases}
\end{equation*}\end{aligned}\]
解释一下 \(\mathbb{a_j}\) 对应了什么。
这是个向量,\(\mathbb{a_j} = \begin{bmatrix} a_{1j} \\ a_{2j} \\ a_{3j} \end{bmatrix}\),表示第 \(j\) 个pattern中,切出的第1种目标木材、第2种目标木材、第3种目标木材的数量。比如,以上述方案1为例,\(a_1 = \begin{bmatrix} 2 \\ 0 \\ 0 \end{bmatrix}\).
(英文的具体解释是 \(a_{ij}\) is the quantity of i-th length piece for the j-th cutting pattern)
而 \(\mathbb{b}\) 就是,需求的3种木材的数量,在这个例子中就是 \(\begin{bmatrix} 30 \\ 20 \\ 40 \end{bmatrix}\)。
求解⚓︎
怎么求解这个问题?
传统方法,当然是暴力枚举。大不了我把所有的pattern都列下来,然后解一个确定模型即可。
\[\min 5x_1 + 5x_2 + ... + 9x_9 + 10x_{10} + 10x_{11} + 10 x_{..}\\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
2x_1 + x_2 + 3x_4 + 2x_5 + x_6 + x_7 + 4x_{10} + 2x_{11} + x_{12} + .. & \geq 30 \\
x_2 + x_5 + 2x_6 + x_7 + x_8 + x_{12} + 3 x_{13} + .. & \geq 20 \\
x_3 + x_7 + x_8 + 2x_9 + x_{11} + x_{12} + .. & \geq 40
\end{cases}
\end{equation*}\end{aligned}\]
这种方法存在的问题
- 如果木材的长度增加,我可以切出来的木板数量一定是指数增长的,上面的式子尚未枚举完全部的切法。
(想象一下,如果你的原材料都是100,150,200的长度木材,但是你需要的都是4,5,9寸这种短木材,你100就可以切:25个4,或者23个4,1 个5 ... 情况很多很多)
- 有一些切法可以明显看出利用率比较低。但是实现的时候很难具体发现哪些利用率低,而是一股脑把所有的切法都写上去。比如你可能会算出一种 \(x_{14}\) pattern,切1个4寸,1个5寸,0个7寸的。这种利用率会比:1个4寸,2个5寸,0个七寸的,浪费很多。
解决这个问题一个最基本也是最重要的思路就是,我们可不可以把一些利用率高、效果好的切法放进去,其他效果不好、利用率低的,就不当作pattern了——隐枚举法。
我们用算法解这个RMP之后,就想,我们能不能得到一个新的Pattern,让原来的结果更好。
逻辑上,和单纯形法类似,每次进-出基,要能实现一次Improve。
Can I get a pattern, to improve the current solution?
区别:
单纯形法的进、出基变量,一开始就已经存在在单纯形表里了。而在列生成里,进基变量不在模型里,而是要你去找的。
解好RMP后,我们就能得到每个约束对应的 Dual Cost(就是常说的影子价格),我们要利用Dual Cost,求解子问题(Sub-Problem),从而找到一些“好”的Pattern(s),这些Pattern(s)不在原来的模型里,但是可以提高当前目标的质量(Improve current Solution). 我们把这些“好”的Pattern加入到RMP中,继续迭代。
英文描述可能更加准确:
In Column Generation, Can we find a \(x_{n + 1}\) such that \(\delta_{n + 1} - c_{n + 1} > 0\)。
这个公式实际就反映单纯形法的“检验数”。
本文语境下,检验数(reduced cost)的表达式统一记为 : \(\delta_{n + 1} - c_{n + 1} = \omega a_{n + 1} - c_j = \sum \omega_i a_{ij} - c_j\)。在此标记下,对于最小化问题,求得最优解的条件是每个变量的检验数,都是非正的。
对偶的意义
这里结合一下前面的数据来解释一下对偶的意义。
案例里约束对应的右端项 \(\mathbb{b} = \begin{bmatrix} 30 \\ 20 \\ 40 \end{bmatrix}\) , \(\omega_1, \omega_2, \omega_3\) 分别对应这三个约束,就是约束 \(i\) 对应的对偶成本(影子价格)。经济意义是,要多切出一个(4寸or,5寸or 7寸)的木板,可以获得的价值。
之所以对生成的列,要求它们满足 \(\delta_{n + 1} - c_{n + 1} > 0\),含义就是:新切出来的目标木料的价值之和,比我多切出这些目标木料所花费的这根原料木板的成本,还要高。
我们的子问题就是,对于一个原料木材,要采纳什么方案(也就是问,要切几个4寸的,几个5寸的,几个7寸的,才能实现上述目标?)。这就是 \(a_{ij}\)。
我们可以写出模型:
\[\max \delta_{n + 1} - c_{n + 1} = \sum_i \omega_i a_{ij} - c_j\\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
\sum^m_{i = 1} a_{ij} l_i \leq L_k \\
a_{ij} \in \mathcal{N^+}
\end{cases}
\end{equation*}\end{aligned}\]
这里的 \(L_k\),对应你原材料的长度的种类,比如9,14,15。如果你从9寸的开始切,\(L_k = 9\),以此类推。每个长度都算一遍。
这里的 \(l_i\) 就是,第 \(i\) 种目标木材的长度(对应4,5,7),\(m\) 对应目标木材的下标。
这里有一种情况,比如说我们 \(L_k\) 有三种情况,会不会每个 \(L_k\) 求下来,目标函数总是 \(\leq 0\) 的。这就意味着:不管我怎么折腾3种原材料,怎么切,都不存在一个更好的方案,使得价值 - 成本 > 0了,也就意味着,我们已经找到了最优解。
if \(\max \sum_i \omega_i a_{ij} - c_k \leq 0, \forall k\),stop. Found Opt Sol.
if \(\max \sum_i \omega_i a_{ij} - c_k > 0\) , pattern is good, add to RMP.
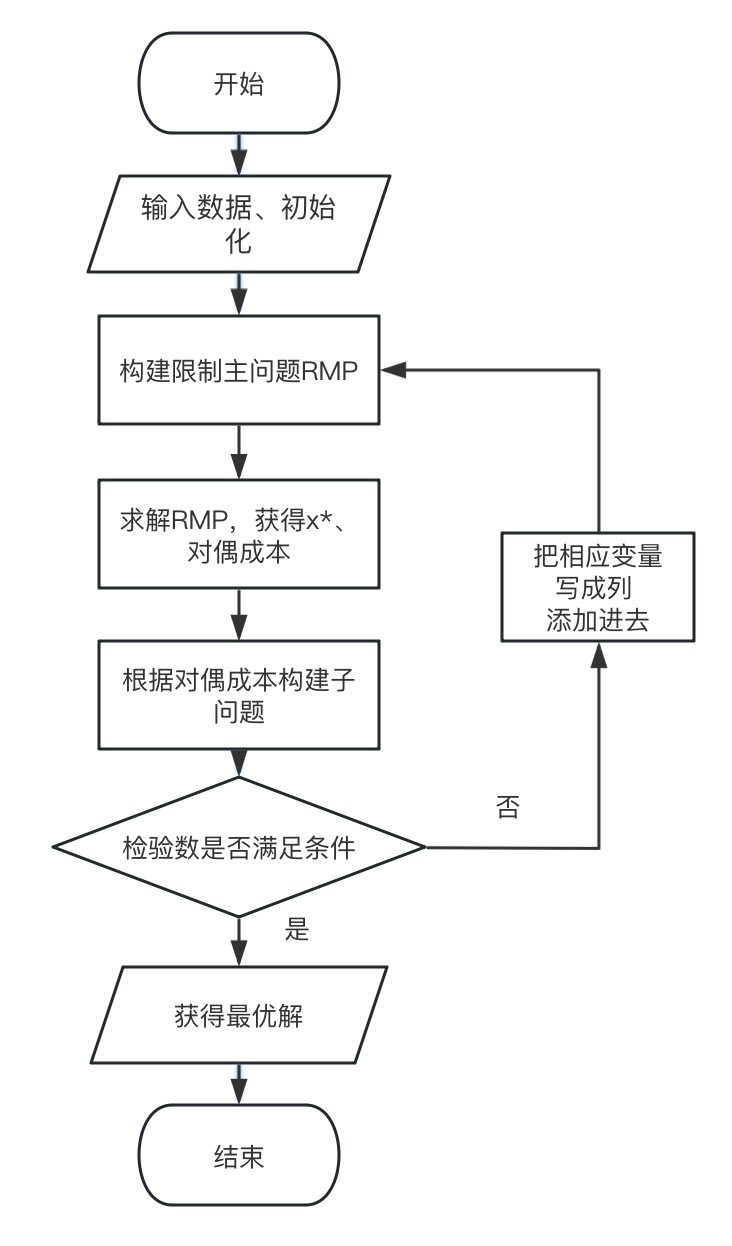
我们可以把整个求解过程罗列如下:
实战⚓︎
- Step 0. Init
\(a_1 = \begin{bmatrix} 2 \\ 0 \\ 0 \end{bmatrix}, a_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, a_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}, c_1 = 5, c_2 = 5, c_3 = 5\),
- Iter 1.
\[\min 5x_1 + 5x_2 + 5x_3 \\ \text{s.t.} \hspace{5pt} a_1 x_1 + a_2x_2 + a_3 x_3 \geq \begin{bmatrix} 20 \\ 40 \\ 50 \end{bmatrix}\]
Solve RMP, \(x^* = \begin{bmatrix} 15 \\ 20 \\ 40 \end{bmatrix}, \omega^* = \begin{bmatrix} 2.5 \\ 5 \\ 5 \end{bmatrix}\)
- Sub Problem 1. (切9寸长的)
\[\max 2.5 a_{1j} + 5 a_{2j} + 5 a_{3j} - 5 \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
4a_{1j} + 5a_{2j} + 7a_{3j} \leq 9 \\
a_{ij} \in Z^*
\end{cases}
\end{equation*}\end{aligned}\]
- Sub Problem 2. (切14寸长的)
\[\max 2.5 a_{1j} + 5 a_{2j} + 5 a_{3j} - 9 \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
4a_{1j} + 5a_{2j} + 7a_{3j} \leq 14 \\
a_{ij} \in Z^*
\end{cases}
\end{equation*}\end{aligned}\]
- Sub Problem 3. (切16寸长的)
\[\max 2.5 a_{1j} + 5 a_{2j} + 5 a_{3j} - 10 \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
4a_{1j} + 5a_{2j} + 7a_{3j} \leq 16 \\
a_{ij} \in Z^*
\end{cases}
\end{equation*}\end{aligned}\]
仔细看:这三个问题实际上都是背包问题。有很多解法。
- Sub Problem 1. Sol \(a_j = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}\), Obj = 2.5
- Sub Problem 2. Sol \(a_j = \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix}\), Obj = 3.5
- Sub Problem 3. Sol \(a_j = \begin{bmatrix} 0 \\ 3 \\ 0 \end{bmatrix}\), Obj = 5
这三个情况下我们发现目标函数都 > 0。我们可以把3个都加到主问题里,也可以只加Obj最大的那个。不同的加法可能对问题求解到最优的收敛速度有影响。
我们把第3个情况加入RMP中。新问题就多了一个决策变量,多了一个pattern,如下。
\[\min 5x_1 + 5x_2 + 5x_3 + 10 x_4, \\ s.t.
a_1 x_1 + a_2x_2 + a_3 x_3 + a_4x_4 \geq \begin{bmatrix} 20 \\ 40 \\ 50 \end{bmatrix}\]
这里就进入下一个迭代。
- Iter 2. 解新的 RMP。
\(x^* = \begin{bmatrix} 15 \\ 0 \\ 40 \\ 20 / 3 \end{bmatrix}, \omega = \begin{bmatrix} 5 / 2 \\ 10 /3 \\ 5 \end{bmatrix}\)。有变化的是新的 dual Cost.
我们继续按照上面的写子问题,注意子问题的目标函数参数也要调整!
- Sub Problem 1. (切9寸长的)
\[\max 2.5 a_{1j} + \frac{10}{3} a_{2j} + 5 a_{3j} - 5 \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
4a_{1j} + 5a_{2j} + 7a_{3j} \leq 9 \\
a_{ij} \in Z^*
\end{cases}
\end{equation*}\end{aligned}\]
- Sub Problem 2. (切14寸长的)
\[\max 2.5 a_{1j} + \frac{10}{3} a_{2j} + 5 a_{3j} - 9 \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
4a_{1j} + 5a_{2j} + 7a_{3j} \leq 14 \\
a_{ij} \in Z^*
\end{cases}
\end{equation*}\end{aligned}\]
- Sub Problem 3. (切16寸长的)
\[\max 2.5 a_{1j} + \frac{10}{3} a_{2j} + 5 a_{3j} - 10 \\
s.t. \begin{aligned}\begin{equation*}
\begin{cases}
4a_{1j} + 5a_{2j} + 7a_{3j} \leq 16 \\
a_{ij} \in Z^*
\end{cases}
\end{equation*}\end{aligned}\]
解下来结果分别是:
-
\(a_j = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}, \delta_j - c_1 = 0\)
-
\(a_j = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix},\delta_j - c_2 = 1\)
-
\(a_j = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix},\delta_j - c_3 = 0\)
我们当然选第二个 \(a_j\) 加入RMP中。
- Iter 3: 这时候RMP有5个变量了。解下来 \(x^* = \begin{bmatrix} 15 \\ 0 \\ 0 \\ 20 / 3 \\ 20 \end{bmatrix}, \delta^* = 322. \omega = \begin{bmatrix} 5 / 2 \\ 10 / 3 \\ 9 / 2 \end{bmatrix}\)
这里继续求解子问题。
-
\(a_j = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, \delta_j - c_1 = 0.82\);
-
\(a_j = \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix}, \delta_j - c_2 = 0.17\);
-
\(a_j = \begin{bmatrix} 0 \\ 3 \\ 0 \end{bmatrix}, \delta_j - c_3 = 0\),
选择 \(a_j = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}\) 加入主问题,继续迭代。
- Iter 4. 解RMP,\(x^* = \begin{bmatrix} 5 \\ 0 \\ 0 \\ 20 \\ 20 \end{bmatrix},\delta = 305, \omega = \begin{bmatrix} 5 /2 \\ 5 /2 \\ 9 /2 \end{bmatrix}\)
继续解子问题~
-
\(a_j = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}, \delta_j - c_1 = -0.5\);
-
\(a_j = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix}, \delta_j - c_2 = 0\);
-
\(a_j = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix}, \delta_j - c_3 = 0\),
我们发现所有的检验数都是非正的。找到最优解了。停止迭代。
备注
这里还需要注意,我们求背包问题的时候,对具体的求解算法没有具体要求,我们甚至不一定要求到子问题的最优解。在实际问题中,最优解的求解反而可能是十分困难的。面对复杂的子问题,我们只要求得一个可以Improve 原问题的解,就够了。这意味着哪怕是启发式的算法、遗传算法之类,同样可以在求解子问题上发挥作用。
一些小问题的处理
- 上面线性松弛问题解出的正好是IP。如果解不到整数解怎么办?在CSP中,一个启发式的思路是向上取整,得到的结果是等价的。(相当于有一些冗余的木料)
- 用你生成的所有变量(e.g. 有6000个),解RMP,不过不再是解LP,而是添加IP约束。一般情况下,IP和LP之间的Gap,会很小。
- 如果方法还是不好,就需要用 Branch-And-Price 去解决这个问题。这个想法就是把 Branch and Bound 和Column Generation结合起来。
问题的延伸和拓展⚓︎
One-Dimension Bin Packing Problem:有一些重量的货物,和一些容量的箱子。需要决定把哪些货物装到箱子里,使得每个箱子里装的货物重量不超过箱子的容量限制,同时最小化用到的箱子的数量。(或者,不同规格的箱子有不同的使用成本,最小化用到的所有箱子的总成本)。
把箱子看成CSP问题中的原料木材,把货物看作是目标木材,货物重量看作目标木材的长度。在这种情境下的 Bin-Packing Problem 实际上就是CSP问题。
Parallel Machine Scheduling (并行机排程)⚓︎
有 \(m\) 台机器,有 \(n\) 项工作 (\(j_1, ...j_n\))。 记工作完成的时间是 \(c_j\),记工作的重要性为 \(w_j\)。需要把这些工作分配到机器上,使得所有工作完成时间的加权和最小。
\[\min \sum^n_{j} w_j c_j\]
同时满足如下假设:
- 工作一旦在某个机器上开始了,就不能中断;
- 同一个工作在所有机器上的加工时间是一样的;
- 每个工作的权重系数一定是大于0的;
模型⚓︎
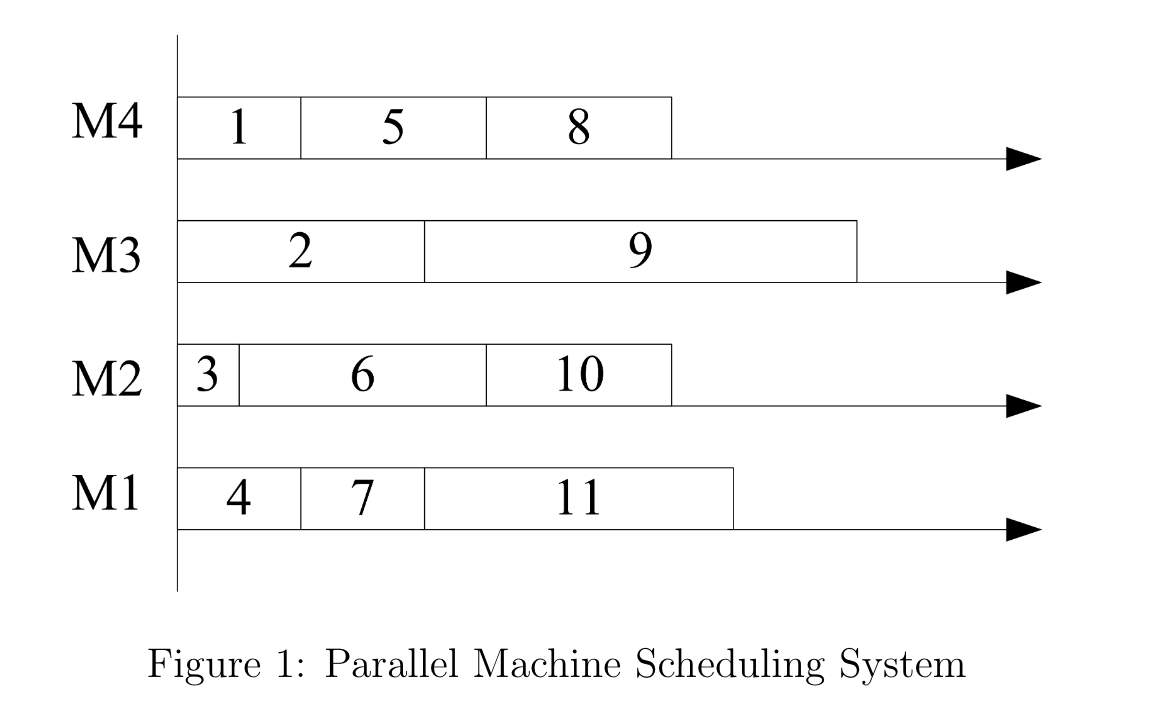
定义一个Schedule:也就是这个机器上进行工作的一个序列。注意,即使机器上进行的是相同的某些工作,这些工作的先后顺序也会构成不同的Schedule。用 \(x_s\) (0-1 Binary)表示这个方案是否被选取;
- 一些参数:
- \(a_{js}\) : 如果工作 \(j\) 在Schedule \(s\) 中,那么就为1,否则为0.以上图为例,\(a_{14}, a_{54}, a_{84} = 1\), \(a_{23}, a_{93} = 1\),以此类推。
如果我们给定一个schedule之后,也就可以算出这个方案对应的成本是多少(因为其完成时间也就可以直接算出来)。而 \(x_s\) 实际上包含了机器的信息。因此我们可以把主问题写成如下形式:
\[\min \sum^s c_s x_s\]
\[\begin{aligned}
\text{s.t.}\begin{equation*}
\begin{cases}
\sum_s a_{js} x_s = 1, \forall j \in J \\
\sum x_s = m \\
x_s \in \{0, 1 \}
\end{cases}
\end{equation*}\end{aligned}\]
主问题的目的就是:从一系列Schedule里选 \(m\) 个出来,满足成本最小的这个需求。
于是新的问题变成了,怎么找一些“好的”方案,形成 \(x_s\) 的这个集合,在这个集合里进行选择,找到最优解呢?
我们可以把主问题的检验数写出来:
\[c^{'}_s = \lambda_0 + \sum_j \lambda_j a_{js} - c_s\]
这里的 \(\lambda_0\) 对应的是第二个约束的对偶成本,因为这个约束与我们生成的列 \(a_{js}\) 无关,所以 \(\lambda_0\) 实际是一个常数。
所以,我们的子问题的目标函数就是看, \(\sum^n_{j = 1} [ \lambda_j - \omega_j (\sum^J_{k = 1} a_{ks}p_k) ] a_{js}\) 的最大值。
备注:一些Generalization
如果把上述第二条假设去掉,可以得到问题更加一般的形式。也就是,同一个工作在不同机器上加工时间不同。建模类似。但是把约束2改成如下,并且 \(x_s\) 针对不同的机器,需包含不同的成本计算方式。
\[\sum x_{is} = 1, \forall i\]
此时,我们记 \(p_{ij}\) 表示第 \(j\) 个工作在第 \(i\) 个机器上的执行时间。
子问题的作用是,给每个机器,从所有的任务中,找一个好的方案分配给它。
所以最终把并行机的排程变成了一个单机的排程问题。
单机排程情况下解的特性
基于假设3,无论选择哪些工作给机器 \(i\) ,这些工作执行的先后顺序,一定满足如下顺序:
\[\dfrac{w_1}{p_{i1}} \geq \dfrac{w_2}{p_{i2}} \geq \dfrac{w_3}{p_{i3}} \geq ... \geq \dfrac{w_n}{p_{in}}\]
也就是先执行的工作的 \(\dfrac{w}{p}\) 一定比后面的工作要大。这被称为:SWPT-rule, (Shortest Weighted Processing Time) 或者 Smith's Method.
Capacitated VRP with CG⚓︎
CVRP的建模方式:Two-index formulation。
仿照前面的建模。
\[\min \sum_s c_s x_s \\ \begin{aligned}\begin{equation*}
s.t. \begin{cases}
\sum a_{js} x_s = 1, \forall \text{customer} \\
\sum x_s \leq 1, \forall \text{vehicle}\\
x_s \in \{0, 1 \}
\end{cases}
\end{equation*}\end{aligned}\]
Reduced Cost: \(\sum_{j \in J} \alpha_j - c_s + \lambda_0\)
Sub Problem: Contrainted Shortest Path Problem
一些想法
上述这些问题的主问题,都变成了一种:
从一系列方案中(按照一定规则)选出一些方案,汇总,从而构造成原来问题的解。
这种建模方式,也可以叫 Set-covering Modeling。是解决一些大规模问题很好用的建模方法。
G 的汇报⚓︎
-
不确定的:很小的偏差。
-
Stochastic Uncertainty: 知道不确定性的规律;
-
Knightian Uncertainty: 不知道不确定性的规律:建立不确定集;
-
分布估计方法:
-
核密度估计
-
线性因子模型
- 控制不确定集合的大小;
- budget Uncertainty Set:
对偶: Duality
- 周一上午10:00, 204