目标规划 (Goal Programming)⚓︎
约 1978 个字 2 张图片 预计阅读时间 7 分钟 总阅读量 次
1. 多目标规划模型⚓︎
-
问题提出:如果只考虑一个主要目标,那么线性规划问题是处理单目标规划的有效方法,但是现实中,一个决策优劣往往需要考虑多个目标,这些目标有时是相互矛盾的,这就是多目标决策的问题,它的特点是对各个目标分级加权和逐级优化,符合人们对一般复杂问题的认识:轻重缓急。 对于初学者,可以视为是线性规划的扩展或推广。
-
有一些线性规划的局限性:固定目标(产品生产出来就一定能销售出去等...)目标规划可以分轻重缓急地评估目标函数、解决问题.
决策变量、约束条件、目标函数
- 正、负偏差变量 \(d^{+}, d^{-}\)这两个至少有一个是0;
-
绝对约束和目标约束,绝对约束是必须严格满足的等式约束和不等式约束,而目标约束是指目标规划特有的,可以把约束右端看作要努力追求的目标值,但允许正负偏差。
-
目标规划的目标函数(达成函数):
- 由各目标约束的偏差变量和相应的优先因子和权系数组成。目标规划追求的是使多目标尽可能都得到满足,偏差尽可能地小,所以目标函数是极小化的;
-
- 优先因子和权系数:
- 对于\(L\)个目标函数\(f_1, f_2,...,f_L\)有主次之分,为此引入优先因子\(P_i(i= 1,2,...,L)\),主次轻重就用优先因子来表示;差别是绝对的;
- 另一种是目标函数之间的差别是相对的,这些目标优先因子相同,他们的重要程度可以通过不同的权系数来表示;
建模过程:类似线性规划的建模:
- 列出绝对约束的约束方程, \(\sum \limits^{n}_{j = 1} a_{ij} x_j \leq (=,\geq) b_i\),其中 \(i\) 代表第 \(i\)个绝对约束;
- 列出目标约束的约束方程, \(\sum \limits^{n}_{j = 1} c_{kj} x_j + d^{-}_k - d^{+}_k = g_k\) ,\(k\) 代表第 \(k\) 个目标约束,目标偏差量、预期期望值等如所示;
- 为各个目标约束确定优先级(优先因子和权系数),给出目标函数的表达式 \(\mathop{\min} { P_l \sum \limits^{K}_{k = 1} (W^{-}_{lk}d^{-}_k + W^{+}_{lk}d^{+}_k), l = 1,2,...,L}\)
其中 \(W^{-}_{lk}\) 和 \(W^{+}_{lk}\) 是\(P_l\) 优先因子对应的个目标的权系数, 对于每种目标取其偏差变量的加权之和、按照优先因子的主次之分逐一对满足对应偏差变量的加权之和最小化目标; 先从 \(P_1\), 开始,然后再从 \(P_2\) 开始...按照最重要的,依次进行;
2. 多目标规划的求解⚓︎
图解法:⚓︎
- 图解法求解目标规划?类似于一个增加约束条件的操作~,优先加入优先因子更高的约束,在此之前需要先把绝对约束的可行域处理得到;
- 如果遇到某个优先因子\(P_{j + 1}\),它的对应解空间为空,此时就只能用上一个优先级的解空间作为最终解空间;
- 如果只有前 \(j\) 个目标约束满足,此时只需要对各个顶点进行比较即可;
单纯形法:⚓︎
- 列初始表时候需要把\(d^{\pm}\) 都列进去,注意检验数的不同,检验数要根据\(P\)(也就是优先因子的情况),然后按照优先因子的大到小比较;
- 用单纯形法迭代,直到检验数都大于0。
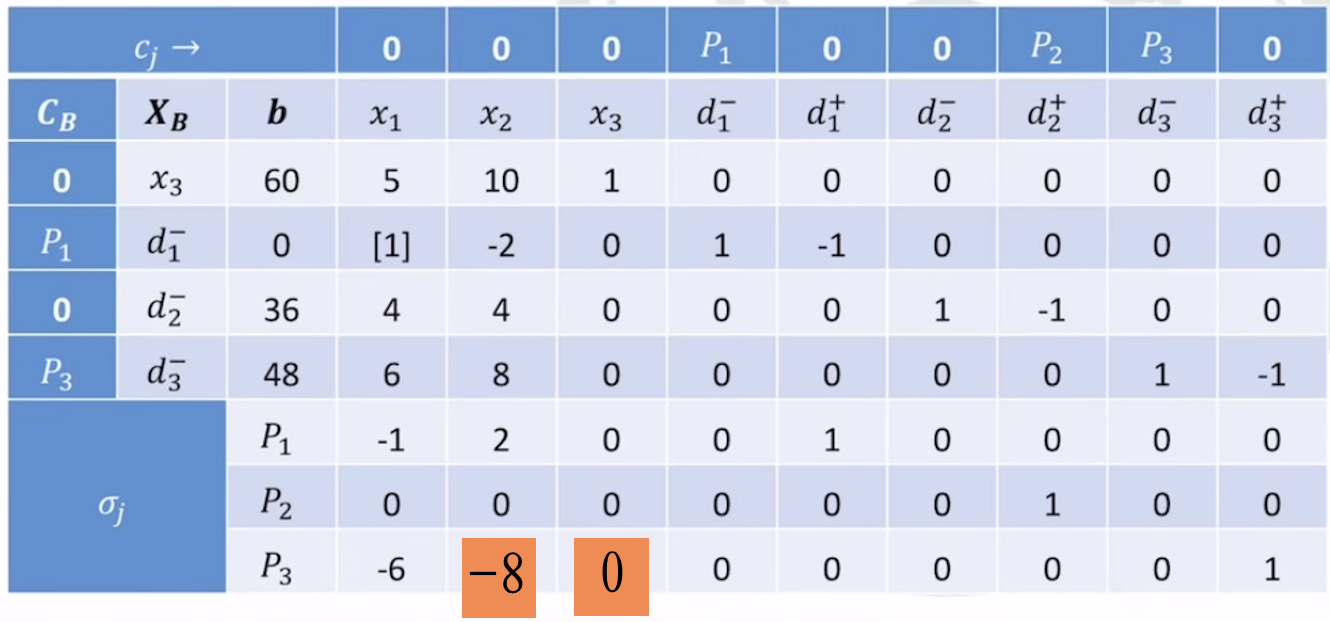
- 某非基变量的检验数都是0,说明有无穷多组最优解;可以对 \(d^{+}_1\) 和 \(d^{+}_3\) 作为入基变量,继续迭代;
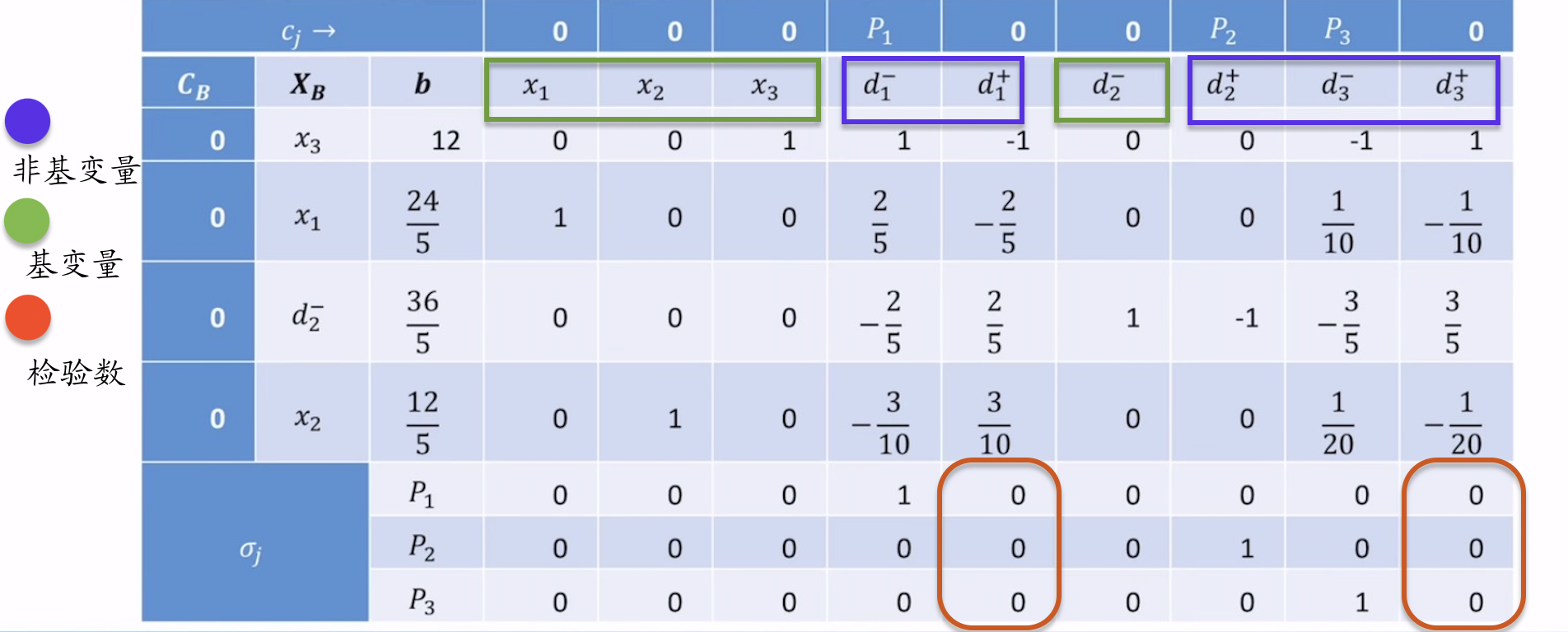
- 在某些问题下,各个检验数字为0但是优先因子对应的系数不全为正数,此时为负数的优先因子的系数表明要求没有全部实现;
- 也可以对优先因子给定权重进行计算(直接转化成一个线性规划问题)
- 优先级分层优化:先对第一级优先因子建模计算 \(\mathop{\min} d^{?}_1\),单纯形法求解看看最优解是否为0,如果是,代表第一层级可以满足,就往第二层级,依次检查;如果有一个层级最优解不是零,说明无法满足这个层级的需求。
示例一⚓︎
某彩色电视机组装工厂,生产\(A、B、C\) 三种规格电视机。装配工作在同一生产线上完成,三种产品装配时的工时消耗分别为\(6\)、\(8\)和\(10\) h。生产线每月正常工作时间为 \(200\) h;三种规格电视机销售后,每台可获利分别为\(500\)元、\(650\)元和\(800\)元。每月销量预计为\(12\)台、\(10\)台、\(6\)台。该厂经营目标如下:
\(p_1\):利润指标定为每月 \(1.6 \times 10^4\) 元; \(p_2\):充分利用生产能力; \(p_3\):加班时间尽可能不超过 24 h; \(p_4\):产量尽量以预期销量为标准。
为确定生产计划,试建立该问题的目标规划模型。
解答:
设生产电视机 \(A\)型为\(x_1\)台,\(B\)型为\(x_2\)台,\(C\)型为\(x_3\)台,该问题的目标规划模型为:
\[\min z = p_1 \cdot d_1^- + p_2 \cdot d_2^- + p_3 \cdot d_3^+ + p_4 (d_4^+ + d_4^- + d_5^+ + d_5^- + d_6^+ + d_6^-)\]
\[s.t. \begin{cases}
500x_1 + 650x_2 + 800x_3 + d_1^+ - d_1^- = 1.6 \times 10^4 \\
6x_1 + 8x_2 + 10x_3 + d_2^+ - d_2^- = 200 \\
d_2^+ + d_3^+ - d_3^- = 24 \\
x_1 + d_4^+ - d_4^- = 12 \\
x_2 + d_5^+ - d_5^- = 10 \\
x_3 + d_6^+ - d_6^- = 6
\end{cases}\]
\[x_1, x_2, x_3 \geq 0; \quad d_i, d_i^+ \geq 0 \quad (i = 1, \dots, 6)\]
- 对于第一个目标,很明显我们希望“低于这个利润指标,目标函数就要更差”,所以目标函数里是 \(p_1 d^+_1\)。
- 对第二个目标,很明显我们肯定希望“如果生产能力没有充分利用,目标函数肯定就更差”,所以目标函数是 \(p_2 d^-_2\)。
- 对第三个目标,我们肯定希望,如果加班时间超过了24h,目标函数肯定就要加上一个惩罚,如果没超过24h,那就不惩罚。所以目标函数写 \(p_3 \cdot d_3^+\)
- 对第四个目标,我们肯定希望的是,“每个产品产量不要距离预期销量差别太大”,也就是 \(p_4(d^+_4+d^-_4)\) 等,以此类推。
示例二⚓︎
已知单位牛奶、牛肉、鸡蛋中的维生素及胆固醇含量等有关数据见下表。 如果只考虑这三种食物,并且设立了下列三个目标:
- 尽量满足三种维生素的每日最小需求量;
- 使每日摄入的胆固醇尽可能少;
- 使每日购买食品的费用尽可能少。
请建立问题的目标规划模型。
| 项目 | 牛奶(500g) | 牛肉 (500g) | 鸡蛋 (500g) | 每日最小需求量 |
|---|---|---|---|---|
| 维生素A/mg | 1 | 1 | 10 | 1 |
| 维生素C/mg | 100 | 10 | 10 | 30 |
| 维生素D/mg | 10 | 100 | 10 | 10 |
| 胆固醇/单位 | 70 | 50 | 120 | - |
| 费用/元 | 1.5 | 8 | 4 | - |
解答: 设三种食物的摄入量分别为 \(x_1, x_2, x_3\)
\[\begin{aligned}
\min & \quad P_1 \left(d_1^- + d_2^- + d_3^-\right) + P_2 d_4^+ + P_3 d_5^+ \\
\text{s.t.} & \quad
\begin{cases}
x_1 + x_2 + 10x_3 + d_1^- - d_1^+ = 1 \\
100x_1 + 10x_2 + 10x_3 + d_2^- - d_2^+ = 30 \\
10x_1 + 100x_2 + 10x_3 + d_3^- - d_3^+ = 10 \\
70x_1 + 50x_2 + 120x_3 + d_4^- - d_4^+ = 0 \\
1.5x_1 + 8x_2 + 4x_3 + d_5^- - d_5^+ = 0 \\
x_i \geq 0, \quad i = 1, 2, 3 \\
d_j^-, d_j^+ \geq 0, \quad j = 1, \ldots, 5
\end{cases}
\end{aligned}\]