图论算法：二分图与匹配问题⚓︎

约 1116 个字 38 行代码 3 张图片预计阅读时间 4 分钟

二分图⚓︎

推荐初学者从这个B站视频开始入门，可以从一个很简单的小问题入手。

weekend dinner scheduling

假设你有A,B,C,D,E,F,G,H,I，共9个好朋友，你想在周五和周六两个晚上请他们吃饭。但是，朋友之间有一些关系，如下所示：

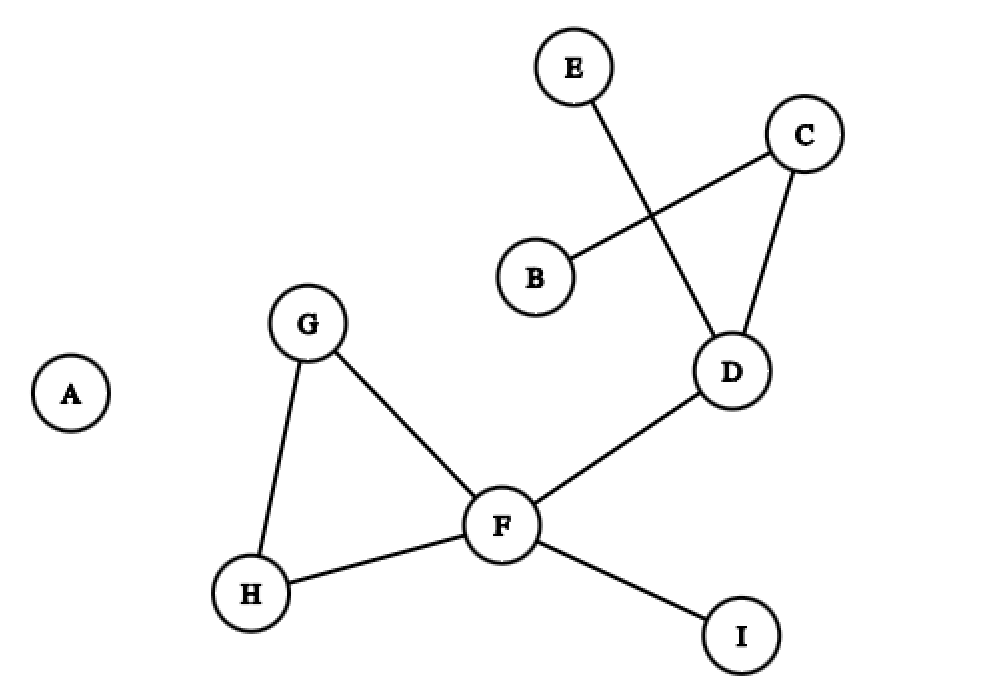
这里的每个边表示相邻的两个朋友互相不喜欢。所以，这两个人必定不能在同一个晚上过来dinner。

用严格的语言表达就是，我们需要安排每个人来参加晚餐的日期（周五或者周六，只有两天），使得：

这里的每个朋友都来参加一次并且仅参加一次晚餐
任何不喜欢的朋友不能在同一天参加晚餐；

上面那个问题，不用多说，可以得到一些有意思的观察：

A人缘很好，没有人不喜欢ta，所以ta可以在周五或者周六任意一天来参加晚餐；
F,G, H 颇有隔阂，他们彼此不喜欢，所以，他们不能在同一天参加晚餐；但是，总共只有2个晚餐，无论如何都不可能在周五或者周六都来参加；比如周五邀请F，那么周六只能邀请G或者H，但是G和H彼此不喜欢，所以，他们不能在同一天参加晚餐。所以，他们只能选择其中一天参加晚餐；

这也就意味着，并不是所有的这种图都能找到解，上图就是一个经典的不可解的情况。

我们要问的问题是：对什么样的图，这样的问题是有解的？

先思考一下下一张图。如果我们缓和GH之间的关系，他们之间不再互相讨厌了，图就变成了：

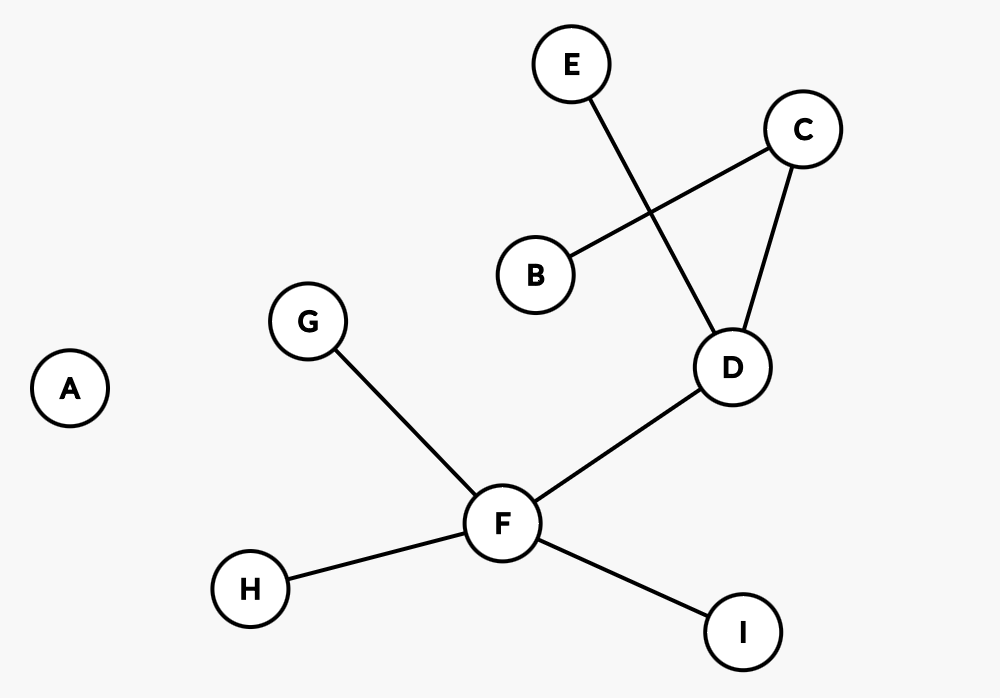
诶，这个时候就可以发现，我们可以找到一个解了。

比如。我们从B开始，依次给所有人安排日期：

B安排在周五，那么C在周六，同理D在周五，而E也在周六；

继续，由于D在周五，所以F在周六，所以GHI都在周五。A随便给ta安排一个时间即可。

所以可以有：

周五	周六
B, D, G, H, I	A, C, E, F

我们实际上把每个节点都划分为两类，一类是周五，一类是周六。所以，这个图实际上是一个二分图(Bipartite Graph)。我们把图画成如下的情形：

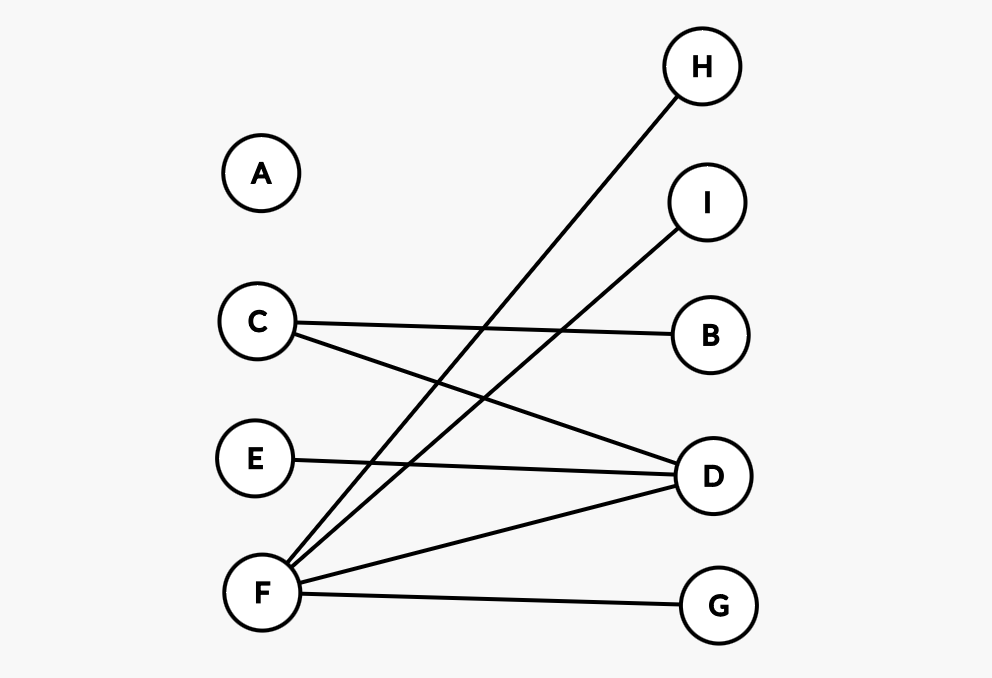
诶，你会发现，左边的每个节点之间，都不互相连接（也就是在左侧节点集合内部不存在相连的边），右边的每个节点之间，也不互相连接；所有的链接都是左边的一个节点连接到右边的节点。

从二分图到图着色⚓︎

现在我们换一个阐述问题的思路。假设我们现在有两个颜色，红色和蓝色。我们希望给每个节点都涂上颜色，使得相邻的节点不能是同一种颜色。这实际上和上面那个安排聚餐日期是一样的，你可以想象成“红色”对应周五聚餐的人；“蓝色”对应周六聚餐的人，以此类推；

我们把“能够用上述规则用两种颜色进行染色”的图，称为 2-colorable 的。可以发现，如果一个图是二分图，那么它一定可以被2-colorable；反过来，如果一个图2-colorable，那么它一定是二分图；同时我们补充，如果一个图没有任何边，那么它也算一个二分图。

现在，我们关注的重点是: 怎么判断一个图是2-colorable的？

如果你有一定注意力，你可以发现，出现3-循环的图一定是不可能2-colorable，比如第一张图GFH的关系；

你也可以发现，出现4-循环的图不一定不能2-colorable，假如ABCD首尾相连，我们可以把AC放在同一天，BD放在同一天，这样也可以2-colorable。

推广第一个结论，你可以发现奇数循环的图一定不能2-colorable。而偶数循环则不一定。

我们也可以写出一个简单的检查二分图染色问题的代码：

def bipartiteGraphColor(graph, start, coloring, color):
    if start not in graph:
        return False, {}

    if start not in coloring:
        coloring[start] = color
    elif coloring[start] != color:
        return False, {}
    else:
        return True, coloring

    if color == 'Sha':
        newcolor = 'Hat'
    else:
        newcolor = 'Sha'

    for vertex in graph[start]:
        val, coloring = bipartiteGraphColor(graph, vertex, coloring, newcolor)
        if val == False:
            return False, {}

    return True, coloring


if __name__ == "__main__":
    graph1 = {
        "A": [],
        "B": ['C'],
        "C": ['B', 'D'],
        "D": ['C', 'E', 'F'],
        "E": ['D'],
        "F": ['D', 'G', 'H', 'I'],
        "G": ['F'],
        "H": ['F'],
        "I": ['F'],
    }

    print(bipartiteGraphColor(graph1, 'A', {}, 'Sha'))

带权二分图匹配问题⚓︎

TODO: 应该会聊聊KM算法...