机组排班问题⚓︎
约 1873 个字 2 张图片 预计阅读时间 6 分钟 总阅读量 次
机组排班问题(Crew Scheduling Problem, CSP),是航空业调度和排班中的一个重要问题。已知一些驾驶舱成员(Cockpit Crew),每个机组有一些可以执飞的航班,称为 Fleet Family,如何在满足诸多约束的情况下,为这些机组安排这些航班,这就是一个典型的机组排班问题。
机组排班问题的输入是一些需要被安排的==航班== (Flight, Flight legs)。如果多个航班连续组成在一起,就形成了一个机组的 执勤日 (Duty Period)。如果我们把多天的执勤日串起来,使得机组能够通过一个循环回到初始的基地,这就形成了一些==航班环== (Pairings),如果多个航班环再串起来,拼成数周乃至一个月的计划,就构成了机组的==月度计划== (Monthly Schedules)。这个过程(Flight legs -> Duty Period -> Pairings -> Monthly Schedules)是机组排班问题的基石。
由上可见,机组排班一个核心的决策就是,给定航班,决定哪些机组分配哪些航班。
- Duty
- 执勤,是指机组成员按照合格证持有人的要求执行的所有任务,包括飞行值勤、置位、备份、培训等;不一定是航班飞行任务,但是对地理位置会有要求;
- Duty Period 执勤日
-
A sequence of flights/duties that can be flown by a single crew over the course of a work day is a duty period. 我们可以把两个flight中间间隔的时间称为 sit time.
执勤日很明显需要遵循一些约束:
- 时空上必须是连续的,也就是航班起降、航班时间必须连贯,三个连续航班,A-B,B-C,C-D是允许的,但是 A-B,C-D 这种是不合理的;两个航班10:30-12:05,16:50-17:40 是允许的,但是 10:30-12:05,11:50-13:40 是不合理的;
- 确保驾驶员不疲劳以应对轮转,连续航班之间有时间约束,(minimum idle time);
- 一天内有最大飞行时间 (Maximum Flying Time)
- ...
评价执勤日的成本,一般可以通过:(1). 飞行时长;(2). 飞行时长占实际时长的比; (3). ...
- Layover (过夜)
- 在两个执勤日之间,机组成员需要过夜(Layover),也就是从一个执勤日结束到另一个执勤日开始的阶段,考虑到前后执勤日的结束和开始机场往往不同,机组不会在前一个执勤日结束就回家,第二天再去另一个地方上班,而可能是在一些指定的过夜机场进行过夜,第二天直接在这个过夜机场开始新的执勤日,或者在这个过夜机场进行置位。
- Pairings(航班环)
-
如果我们将多个执勤日和中间的过夜行为串联起来,使得机组能够从一个Base出发,经过多天执勤,最终返回相同的Base,那么这一串的执勤日和过夜就构成了一个 Pairing。
Pairing 面临的约束就更加多了。首先:
- 最多执勤任务数量 (maximum number of duties);
- 执勤的最小/最大休息时间;
- Pairing的最长持续时间 (又被称为 TAFB, Time Away From Base,因为一般Pairing最后要回到开始的机场)
- 单日执勤时长加倍休息约束等;
- Schedules
-
相当于上述汇总:
Flights - (sit time) - Flight ===> Duty Period
Duty Period - (layover) - Duty Period ===> Pairings
Pairings - (time off) - Pairings ===> Schedule
Crew Pairing Problem⚓︎
机组人员配对问题的模型通常被表述为集合划分问题 (Set Partition Problem),在这个问题中,我们希望找到可行Pair的一个成本最小的子集,使得每个航段恰好包含在一个选定的配对中。
设 \(F\) 为需要覆盖的航班航段集合,\(P\) 为所有可行的配对集合。决策变量 \(y_p\),如果配对 \(p\) 包含在解决方案中,则等于 1,否则为 0。如果航班 \(i\) 包含在配对 \(p\) 中,则约束矩阵第 \(i\) 行的列 \(p\) 为 1,否则为 0。
\[\begin{align}
\min \quad & \sum_{p \in P} c_p\, y_p \\
\text{s.t.}\quad & \sum_{p : i \in p} y_p = 1 && \forall i \in F,\\
& y_p \in \{0,1\} && \forall p \in P.
\end{align}\]
注意了,这种配对是可以逐层叠加的,可以用于机组人员配对优化的所有三个阶段 (比如 从 daily 的,到 weekly 的,到monthly的)。这些模型的不同之处在于定义问题约束的航班集合 \(F\)。
举个例子
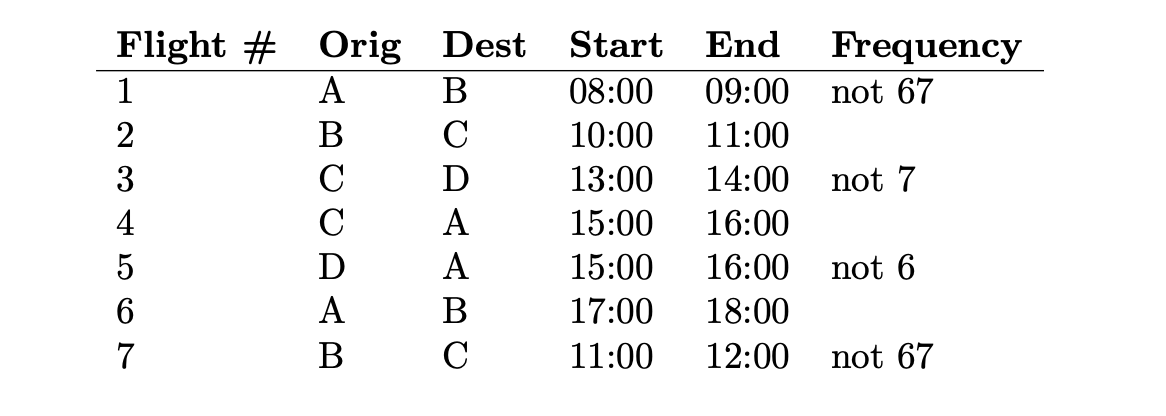
总共有7个航班,其OD分别给出,也包括其起飞和结束时间和其在一周内的安排。
我们可以以天为单位进行pair,比如
\[\begin{aligned}
D_1 &= \{1\}, & D_2 &= \{2\}, & D_3 &= \{3\}, & D_4 &= \{4\},\\
D_5 &= \{5\}, & D_6 &= \{6\}, & D_7 &= \{7\}, & D_8 &= \{1,2\},\\
D_9 &= \{1,7,3\}, & D_{10} &= \{2,3\}.
\end{aligned}\]
为什么 \(D_9 = \{1, 7, 3\}\),可以看出你一周每天(除了67)都可以早上8-9从A到B,早上11-12从B到C,下午13-14从C到D,在空间和时间上都是能够保持连续的。
我们可以把这些 \(D_x\) 继续进行pair,比如假设我们令A,C,D为可过夜的机场,(也就是某天不能以B结束),那么可以把 \(D_x\) 继续pair成:
\[\begin{aligned}
P_1 &= \{D_4,\, D_8\}, &
P_2 &= \{D_9,\, D_5\}, &
P_3 &= \{D_5,\, D_6,\, D_{10}\} \\
P_4 &= \{D_4,\, D_6,\, D_7\}, &
P_5 &= \{D_1,\, D_7,\, D_4\}, &
P_6 &= \{D_5,\, D_7,\, D_9\}.
\end{aligned}\]
这里还要剔除一下 \(P_6\) 因为 \(D_5, D_7, D_9\) 中有重复包含的 flight 7。
这里还需要注意,你其实也可以找到 \(\{ D_1, D_2, D_4 \}\) 这个组合,但是你可以发现这和 \(P_1\) 实际上是重合的。所以保留一个(或者保留实际成本最小的那个)就行了。
此时我们有 5 个 周维度的备选项,每一个都是一个决策变量,\(y_i\) 表示下标为 \(i\) 的周度规划是否被选中(0-1 Binary)。而约束条件下的系数就是表示当前周度规划是否包括了某个航班,注意目标函数的系数是随便取的,实际应该计算后得出。
\[\begin{aligned}
\min \;& 4y_{1} + 4y_{2} + 4y_{3} + 4y_{4} + 5y_{5} \\[4pt]
\text{s.t. }\;& y_{1} + y_{2} + y_{5} = 1 & (\text{flight }1)\\
& y_{1} + y_{3} = 1 & (\text{flight }2)\\
& y_{2} + y_{3} = 1 & (\text{flight }3)\\
& y_{1} + y_{4} + y_{5} = 1 & (\text{flight }4)\\
& y_{2} + y_{3} = 1 & (\text{flight }5)\\
& \phantom{y_{2}+}\,y_{3} + y_{4} = 1 & (\text{flight }6)\\
& y_{2} + y_{4} + y_{5} = 1 & (\text{flight }7)\\[6pt]
& y_{j} \in \{0,1\} & j = 1,\dots,5.
\end{aligned}\]
实际建模的时候可能还有Pay Balance约束,比如在每个CrewBase的成本必须在某个阈值之间,比如在A,C,D的成本必须控制在一定范围内:
\[\begin{aligned}
3 \;\le\; 4y_{2} + 3y_{5} \;\le\; 6 &\quad (\text{Crewbase A})\\
0 \;\le\; 3y_{1} + 3y_{4} \;\le\; 5 &\quad (\text{Crewbase C})\\
3 \;\le\; 4y_{3} \;\le\; 6 &\quad (\text{Crewbase D}).
\end{aligned}\]
最优解是选择 \(P_3 = \{D_5,\, D_6,\, D_{10}\}\) 和 \(P_5 = \{D_1,\, D_7,\, D_4\}\)。
为了编制成周度计划,还需要一些额外的置位(因为有些航班是仅在特定日期飞,也就是:

Pair Generation⚓︎
上面的问题建立在给定一系列 Pair 的基础之上(天度的Pair),但是如何生成这些 Pair 并没有详细地展开。这里我们会讨论如何生成这些 Pair,以及一些基础的建模工具和方法。