Lot Sizing Problem 批量生产问题⚓︎
约 1990 个字 1 张图片 预计阅读时间 7 分钟 总阅读量 次
是生产管理、库存管理中一类常见的优化问题,旨在求解未来一段时间内的生产或订购决策,在满足需求的前提下使得总成本最小。其应用场景很多,导致有很多样化的约束。我们这部分只会展开一些比较基础和简单的问题。
需要注意的是,如果是Uncapacitated Lot Sizing Problem (ULSP),是可以多项式时间内用动态规划直接求解。如果存在产能约束,那么问题就变成了一个NP-hard问题。我们首先讨论没有容量限制的ULSP问题。
问题描述⚓︎
给定一个计划周期(planning horizon),这个计划周期由若干个离散的时间段(period)组成,每个时间段都有对应的产品市场需求量(demand),生产企业需要生产足够多的产品来满足市场需求。在生产中,需要考虑开机成本(setup cost)、单位生产成本(unit production cost)以及 单位仓储成本(inventory holding host)。
其中,开机成本属于固定成本(fixed cost),因为开机之后,当期可以生产任意数量的产品;而单位生产成本和单位仓储成本则属于变动成本(variable cost),因为它们由当期产量而定。不同时间段的开机成本、单位生产成本和单位仓储成本可能不同(time-varying)。
生产企业则需要决策,在哪些时间段开机进行生产以及产量为多少,使得市场需求被完全覆盖,目标则为最小化总成本(开机成本+生产成本+仓储成本)。 可以用符号表示为:
| 标记 | 含义 |
|---|---|
| \(T = \{1, 2, \dots, m\}\) | 计划周期(时间段集合) |
| \(d_t\) | 产品在时间段 \(t \in T\) 的需求量 \(d_t\) |
| \(s_t\) | 在时间段 \(t \in T\) 的开机成本 \(s_t\) |
| \(p_t\) | 在时间段 \(t \in T\) 的单位生产成本 \(p_t\) |
| \(h_t\) | 在时间段 \(t \in T\) 的单位仓储成本 \(h_t\) |
决策变量⚓︎
\(y_t\): 是否在时间段 \(t \in T\) 开机生产;0-1变量;
\(x_t\) : 时间段 \(t \in T\) 的生产量
\(q_t\) : 时间段 \(t \in T \cup \{ m + 1 \}\) 开始时的库存量。
注意,我们引入了一个虚拟的时间段 \(m + 1\),\(q_{m+1}\) 的含义就是时间段 \(m + 1\) 开始时的库存量(也就是 \(m\) 时间段结束时的库存量)。
目标函数⚓︎
\[\min. \sum_{t \in T} s_t y_t + \sum_{t \in T} p_t x_t + \sum_{t \in T} h_t q_{t+1}\]
约束条件⚓︎
\[\begin{aligned}
\begin{cases}
\begin{align}
q_{t+1} &= q_t + x_t - d_t \quad \forall t \in T \quad \quad \\
q_1 &= 0 \quad \quad \\
q_{m+1} &= 0 \quad \quad \\
q_t &\leq M_t y_t \quad \forall t \in T \quad \quad \\
y_t &\in \{0, 1\} \quad \forall t \in T \quad \quad \\
x_t &\geq 0 \quad \forall t \in T \quad \quad \\
q_t &\geq 0 \quad \forall t \in T \cup \{m+1\}
\end{align}
\end{cases}
\end{aligned}\]
| 标记 | 含义 |
|---|---|
| (1) | 库存平衡约束(inventory balance equations)。 |
| (2)(3) | 分别规定了仓库的初始(第一期)库存量和最终(最后一期)库存量为0。 |
| (4) | 耦合约束,规定了若在时间段 \(t\) 不开机,则当期产量为0 |
| (5)(6)(7) | 规定了决策变量的值域。 |
这是一个比较简单的模型。Wagner and Whiti 在1958年就提出了这个模型。
最短路法视角下的描述⚓︎
Evans 提出用有向无环图来刻画 USILSP,然后通过求解最短路问题(Shortest Path Problem, SPP)来求解 ULSP。在图中,一个结点(node)代表一个时间段,共有 \(m + 1\) 个时间段(存在一个虚拟时间段)。从结点 \(t\) 到结点 \(\tau\) 的弧代表在时间段 \(t\) 生产从时间段 \(t\) 到时间段 \(\tau - 1\) 的所有需求量。求解 USILSP 等价于求解从结点 1 到结点 \(m + 1\) 的最短路径。我们可以结合下图来理解:
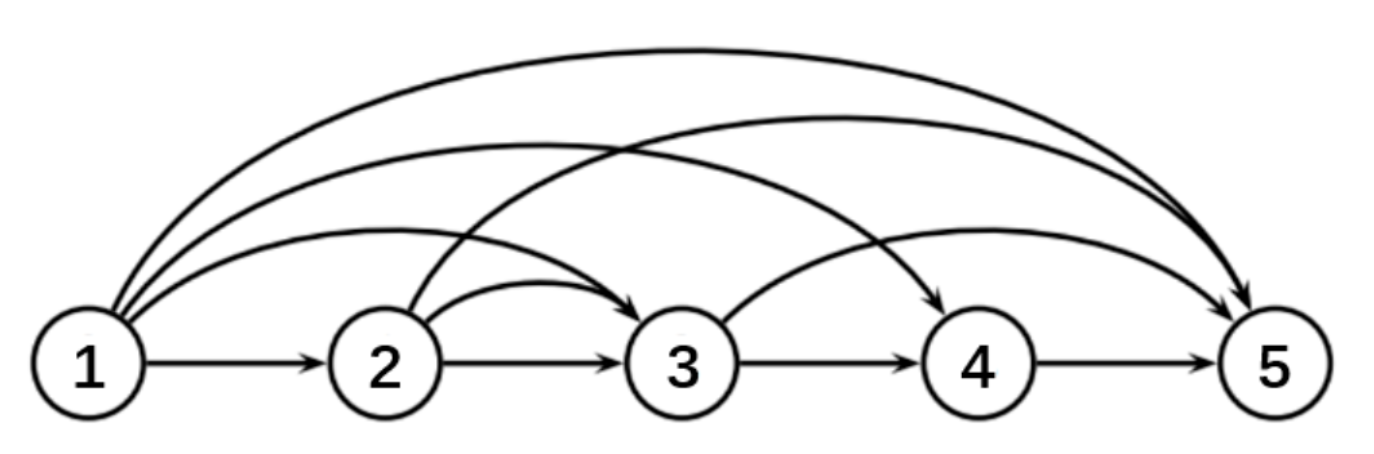
图中的5个结点代表五个时间段(\(m = 4\)),其中结点 5 为虚拟时间段。弧的数量为 \(\frac{m(m+1)}{2}\),此处 \(m = 4\),所以图中有10条弧。图中的每条弧代表一个生产选项(production option),例如弧 (1,5) 表示在时间段 1 开机且生产量为时间段 1 到时间段 4 的需求量之和。现在图中没有弧值,这里的弧值其实是生产选项对应的成本,关于弧值的计算方式见后文。
我们需要做的就是找到一条从结点 1 到结点 5 的最短路径,从最短路径中可以推算出计划周期内总成本最低的生产方案。令 \(v_{t\tau}\) 为在时间段 \(t\) 生产 \(d_t + d_{t+1} + \cdots + d_{\tau-1}\) 件产品的变动成本(生产成本 + 仓储成本)之和,则有弧值的计算方式如下:
\[v_{t\tau} = p_t \sum_{i=t}^{\tau-1} d_i + \sum_{i=t}^{\tau-2} h_i \sum_{j=i+1}^{\tau-1} d_j \quad \forall t = 1, \dots, m, \tau = t+1, \dots, m+1\]
所以给出问题的目标函数:
\[\min. \sum_{t=1}^{m} s_t y_t + \sum_{t=1}^{m} \sum_{\tau=t+1}^{m+1} v_{t\tau} z_{t\tau}\]
\[\begin{aligned}
\begin{cases}
\begin{align}
\sum_{\tau=2}^{m+1} z_{1\tau} &= 1 \quad \quad \\
\sum_{i=1}^{t-1} z_{i\tau} - \sum_{\tau=t+1}^{m+1} z_{t\tau} &= 0 \quad \forall t = 2, \dots, m \quad \quad\\
\sum_{\tau=t+1}^{m+1} z_{t\tau} &\leq y_t \quad \forall t = 1, \dots, m \quad \quad \\
y_t &\in \{0,1\} \quad \forall t = 1, \dots, m \quad \quad\\
z_{t\tau} &\in \{0,1\} \quad \forall t = 1, \dots, m, \tau = t+1, \dots, m+1
\end{align}
\end{cases}
\end{aligned}\]
有产量限制的多商品Lot-Sizing-Problem⚓︎
New construction heuristic for capacitated lot sizing problems
这里我们给出一个更加复杂一点,同时具有一定普适性的建模。我们的问题描述如下:
- 需要给多个商品制定生产计划;
- 每个时间段内每个商品的产量是有限制的;
- 每个周期内,商品可以正常生产,也可以加班生产,两种情况下的生产成本是不同的,但是正常生产 + 加班生产的产量都是有限制的;
- 每个产品开始生产后,需要一定的setup时间;
- 与之前的LSP问题一样,每个商品存储在仓库中也有成本;
| Parameters | Description |
|---|---|
| \(i\) | 商品编号 \((i = 1, \dots, P)\) |
| \(t\) | 时间周期编号 \((t = 1, \dots, T)\) |
| \(sc_i\) | 商品 \(i\) 的启动成本 |
| \(hc_i\) | 商品 \(i\) 的持有成本 |
| \(oc\) | 加班成本 |
| \(d_{it}\) | 商品 \(i\) 在周期 \(t\) 内的需求 |
| \(l_{i0}\) | 商品 \(i\) 在第一个周期 \((l_{i0} = 0)\) 时的库存 |
| \(C_t\) | 周期 \(t\) 内的正常生产量 |
| \(st_i\) | 商品 \(i\) 的启动时间 |
| Decision variables | Description |
|---|---|
| \(X_{it}\) | Production amount of item \(i\) in period \(t\) |
| \(Y_{it}\) | $ \left{ \begin{array}{ll} 1 & \text{if item } i \text{ is produced in period } t \ 0 & \text{otherwise} \end{array} \right. $ |
| \(I_{it}\) | Inventory level of item \(i\) at the end of period \(t\) |
| \(O_t\) | Overtime capacity used in period \(t\) |
\[\min Z = \sum_{i=1}^{P} \sum_{t=1}^{T} (sc_i \cdot Y_{it} + hc_i \cdot I_{it}) + \sum_{t=1}^{T} oc \cdot O_t\]
subject to.
\[\begin{aligned}
\begin{cases}
\begin{align}
I_{it} = I_{i(t-1)} + X_{it} - d_{it} \quad \forall i, t \quad \\
\sum_{i=1}^{P} (X_{it} + st_i \cdot Y_{it}) \leq C_t + O_t \quad \forall t \quad \\
X_{it} \leq \left( \sum_{\tau=1}^{T} d_{i\tau} \right) \cdot Y_{it} \quad \forall i, t \quad \\
Y_{it} \in \{0, 1\}, \quad I_{it}, X_{it}, O_t \geq 0 \quad \forall i, t
\end{align}
\end{cases}
\end{aligned}\]
目标函数:最小化生产计划的总成本,通过最小化启动成本之和和库存持有成本之和,以及加班成本之和来实现。
待整理:
Objective function (1) minimizes the total cost of the production plan, expressed by the sum of setup costs and inventory holding costs for all products over all periods and overtime costs in all periods. It is subject to inventory balance constraints (2), capacity constraints (3) and setup constraints (4), which force setups in periods where production amounts are positive. We assume that demand and production quantities are measured in capacity units, so the production coefficients in (3) are one. The usual non-negativity and binary constraints are denoted by