概率基础⚓︎

约 2846 个字 3 张图片预计阅读时间 9 分钟总阅读量次

从零开始 ...⚓︎

概念	辨析
基本事件	由一个样本点组成的单点集.如:{H},{T}
必然事件	样本空间 S 是自身的子集，在每次试验中总是发生的，称为必然事件。
复合事件	由两或两个以上的基本事件复合而成的事件，称为复合事件. 如: E3中
不可能事件：空集	不包含任何样本点，它在每次试验中都不发生，称为不可能事件。

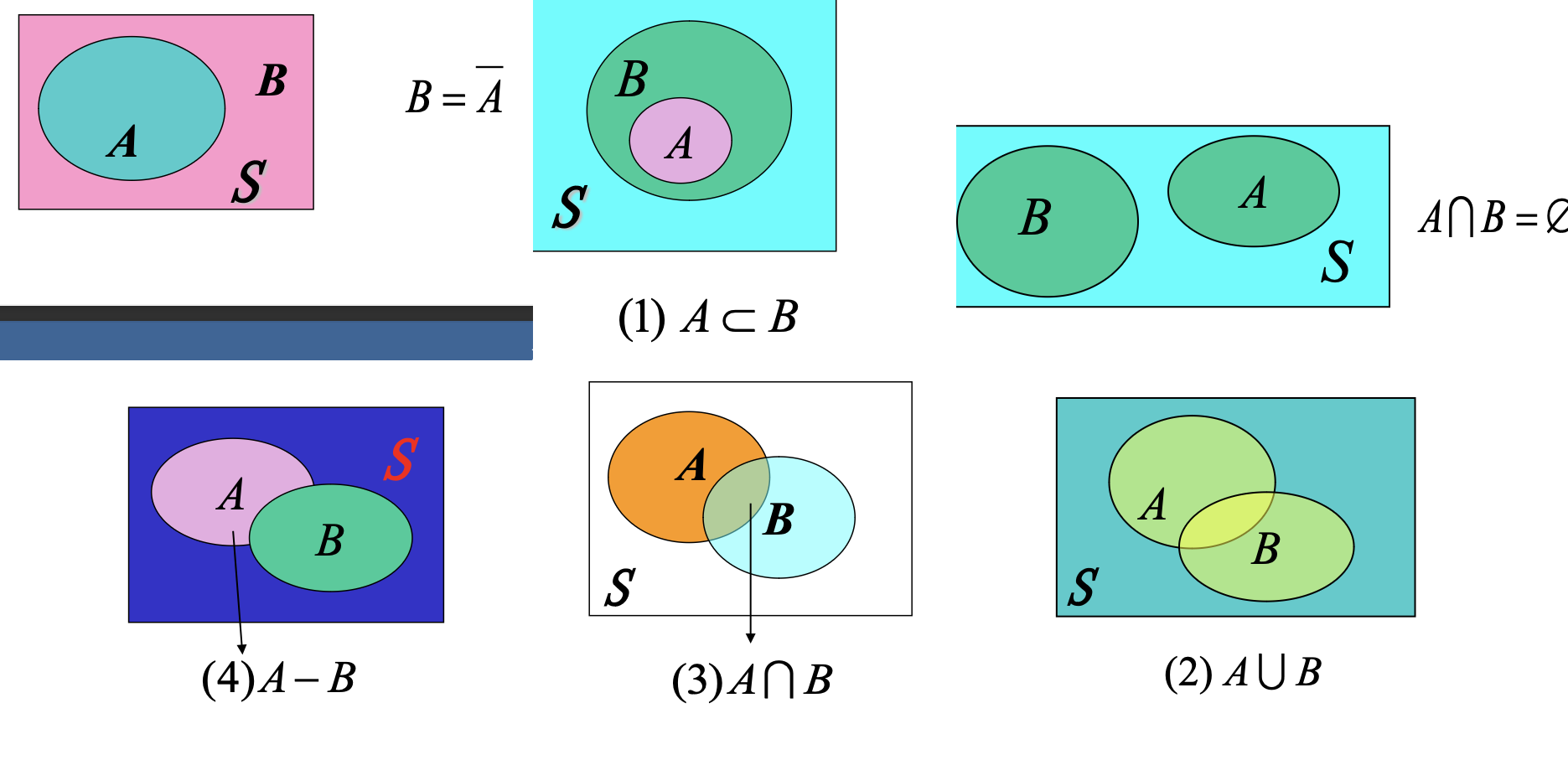
若事件 A 发生必然导致事件 B 发生, 则称事件 B 包含事件A, 记作 A B；
事件$C$ 表示 "事件$A$与$B$同时发生"，事件$C$称为$A$与$B$的交（积事件），记作$A \cap B$

\[(AB), \quad A \cap B = \{x \mid x \in A \text{ 且 } x \in B\}\]

类似地，事件$\bigcap_{k=1}^{\infty} A_k$为可列个事件$A_1, A_2, \dots$的交。

这里要记好了，$AB$ 这个表述，表示 $A$ 与 $B$同时发生这个事件！！

事件$A-B$ 称为$A$与$B$的差；当且仅当$A$发生，$B$不发生时，事件$A-B$发生。即：

\[A-B = \{x \mid x \in A \text{ 且 } x \notin B\} = A\bar{B} = A-AB\]

显然：$A-A=\emptyset$, $A-\emptyset=A$, $A-S=\emptyset$

互不相容事件（互斥事件）

若$A \cap B = \emptyset$，则称$A$与$B$是互不相容的，或互斥的，即$A$与$B$不能同时发生。

(1) 基本事件是两两互不相容的，即样本点是互不相容的，事件$A$与$B-A$是互不相容的。

(2) 若用集合表示事件，则$A, B$互不相容即为$A$与$B$是不相交的。

交换律

\[A \cup B = B \cup A; \quad A \cap B = B \cap A.\]

结合律：

\[(A \cup B) \cup C = A \cup (B \cup C),\]

\[(AB)C = A(BC)\]

分配律：

\[A \cup (B \cap C) = (A \cup B) \cap (A \cup C);\]

\[A \cap (B \cup C) = (A \cap B) \cup (A \cap C).\]

德 · 摩根律：

\[\overline{A \cup B} = \overline{A} \cap \overline{B}; \quad \overline{A \cap B} = \overline{A} \cup \overline{B}.\]

\[\overline{A \cup B} = \overline{\{\text{A、B至少发生一个}\}} = \{\text{A、B都不发生}\} = \overline{A} \cap \overline{B}.\]

摩根律推广：

\[\overline{\bigcup_i A_i} = \bigcap_i \overline{A_i}, \quad \overline{\bigcap_i A_i} = \bigcup_i \overline{A_i}.\]

频率到概率⚓︎

从频率到概率

将一试验$E$在相同的条件下重复进行$n$次，如果事件$A$发生了$n_A$次，则比值$n_A/n$称为事件$A$发生的频率，记为$f_n(A)$。

频率的基本性质：

$f_n(A) \ge 0$；（非负性）
$f_n(S) = 1$；（规范性）
可加性：对互斥事件$A,B$，有

\[f_n(A \cup B) = f_n(A) + f_n(B)\]

频率的稳定值 $P(A)$ ，反映了事件 $A$ 在一次试验中发生的可能性大小，称 $P(A)$ 为事件 $A$ 的概率。

（稳定）

设$S$为样本空间，$A$为事件，对每一事件$A$赋予一实数$P(A)$，如果$P(A)$满足如下三条公理，则称$P(A)$为事件$A$的概率。

(1) 非负性：$P(A) \ge 0$

(2) 规范性（正则性）：$P(S)=1$；

(3) 对两两互斥事件$A_i \ (i=1,2,\dots)$，有：

可列可加性：$P\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} P(A_i)$

概率的基本性质：重点：

有限可加性，$A_i$ 互不相容！

\[P\left(\bigcup_{i=1}^{n} A_i\right) = \sum_{i=1}^{n} P(A_i)\]

证：令$A_{n+1}=A_{n+2}=\dots=\emptyset$，则有$A_i A_j=\emptyset$，由可列可加性可得：

\[P\left(\bigcup_{i=1}^{n} A_i\right) = P\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} P(A_i) = \sum_{i=1}^{n} P(A_i) + \sum_{i=n+1}^{\infty} P(A_i) = \sum_{i=1}^{n} P(A_i)\]

可列可加性：$P\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} P(A_i)$

对任一事件$A$， $P(A) \le 1$.

若$A \subset B$，则有：

$P(B-A) = P(B) - P(A)$;

$P(B) \ge P(A)$.

加奇减偶公式

可以作如下推广：

\[P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(AB) - P(AC) - P(BC) + P(ABC)\]

\[P(A_1 \cup A_2 \cup \dots \cup A_n) =\]

\[\sum_{i=1}^{n} P(A_i) - \sum_{1 \le i < j \le n} P(A_i A_j) + \sum_{1 \le i < j < k \le n} P(A_i A_j A_k) + \dots + (-1)^{n-1} P(A_1 A_2 \dots A_n)\]

这个式子称为 "加奇减偶公式"。

==加法公式==是它的简单版：

\[P(A \cup B) = P(A) + P(B) - P(AB)\]

例1： 设$A, B$为两个事件，且$P(A)=0.5, P(B)=0.3, P(AB)=0.2$，求下列各事件的概率。

(1) $\overline{AB}$; (2) $\overline{A}\overline{B}$; (3) $\overline{A}B$; (4) $\overline{A \cup B}$。

解：

(1) $P(\overline{AB}) = 1 - P(AB) = 1 - 0.2 = 0.8$

(2) $P(\overline{A}\overline{B}) = P(\overline{A \cup B})$ （根据德摩根律）

$= 1 - P(A \cup B)$$$$= 1 - [P(A) + P(B) - P(AB)]$

$= 0.4$

(3) $P(\overline{A}B) = P(B-A)$ （根据事件差的定义）

$= P(B) - P(AB)$

$= 0.3 - 0.2 = 0.1$

(4) $P(\overline{A \cup B}) = P(\overline{A}\overline{B}) = 0.4$ （根据德摩根律和第(2)小题的结果）

古典概型⚓︎

若随机试验有以下两个特点，这类随机现象的概率模型叫做古典概型：

(1) 样本空间中只有有限个样本点，即$S = \{e_1, e_2, \dots, e_n\}$

(2) 试验中每个基本事件（样本点）的发生是等可能的，即$P(e_1) = P(e_2) = \dots = P(e_n)$。

加法原理 / 乘法原理⚓︎

（加法原理）：完成一件工作，有$m$类方法，而第1类方法有$n_1$种方法，第2类方法有$n_2$种方法，…，第$m$类方法有$n_m$种方法，任选一种此工作就完成，那么完成这项工作共有$N=n_1+n_2+\dots+n_m$种不同的方法。

（乘法原理）：完成一件工作，需要$m$个步骤，而第1步有$n_1$种方法，第2步有$n_2$种方法，…，第$m$步有$n_m$种方法，依次完成这$m$步时这项工作才完成，那么完成这项工作共有$N=n_1 \times n_2 \times \dots \times n_m$种不同的方法。

几何概型⚓︎

(1) 样本空间$S$是一个几何区域，这个区域的大小是可以度量的（如长度、面积、体积等），并把对$S$的度量记作$m(S)$；

(2) 向区域$S$内任意投掷，投掷落点在区域内任一个点处都是等可能的，或者说投掷落点在$S$中的区域$A$内的可能性与$A$的度量成正比，而与$A$的位置、状态及形态无关；

条件概率⚓︎

设试验$E$的样本空间为$S$， $A, B$是事件，要考虑在$A$已经发生的条件下$B$发生的概率，这就是条件概率，记为$P(B|A)$。

例1： 将一枚硬币掷两次，观察其出现正反面的情况。设$A$—“至少有一次正面”， $B$—“两次掷出同一面”，求：$A$发生的条件下$B$发生的概率。

1. 定义

设 $A$，$B$ 是两个事件，且 $P(A) > 0$，称 $P(B \mid A)$ 为在事件 $A$ 发生的条件下事件 $B$ 发生的条件概率。

\[ P(B \mid A) = \frac{P(AB)}{P(A)} \]

直观含义：求这个条件概率，$A$发生是一大前提，在这个空间中求$B$发生的概率，因此$P(B|A) = P(AB)/P(A)$.

2. 性质

条件概率符合概率定义中的三条公理，即

非负性：对于每一个事件 $B$，有 $P(B \mid A) \ge 0$。
规范性：$P(S \mid A) = 1$。
可列可加性：设 $B_1$，$B_2$，$\dots$ 两两互不相容，则

\[ P\left( \bigcup_{i=1}^{\infty} B_i \mid A \right) = \sum_{i=1}^{\infty} P(B_i \mid A) \]

此外，条件概率具有无条件概率类似性质.例如：

(1) $P(\varnothing \mid A) = 0$.

(2) 设 $B_{1},B_{2},\ldots,B_{n}$ 两两互不相容，则

\[ P\left( \bigcup_{i=1}^{n} B_{i} \mid A \right) = \sum_{i=1}^{n} P(B_{i} \mid A). \]

(3) $P(\neg B \mid A) = 1 - P(B \mid A)$.

(4) $P(B \cup C \mid A) = P(B \mid A) + P(C \mid A) - P(BC \mid A)$.

乘法公式⚓︎

一般，设 $A_{1}, A_{2}, \ldots, A_{n}$ 是 $n$ 个事件 $(n \geq 2)$，且 $P(A_{1}A_{2} \ldots A_{n-1}) > 0$，则有乘法公式：

\[P(A_{1}A_{2} \ldots A_{n}) = P(A_{1}) P(A_{2} | A_{1}) \ldots P(A_{n-1} | A_{1}A_{2} \ldots A_{n-2}) P(A_{n} | A_{1}A_{2} \ldots A_{n-1})\]

全概率公式⚓︎

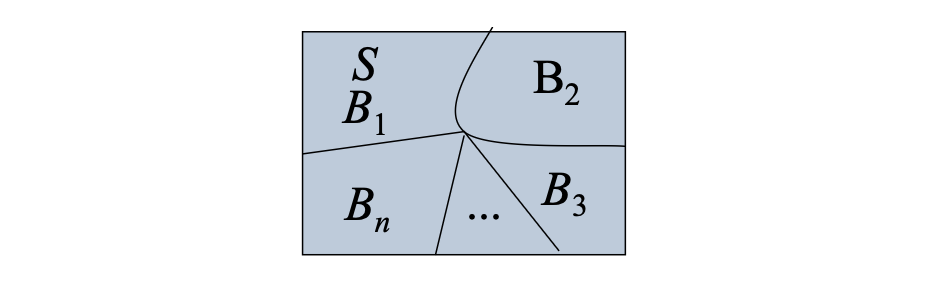
样本空间的划分：

定义：设 $B_1, B_2, \cdots, B_n$ 是一组事件，它们构成样本空间 $S$ 的一个划分，当且仅当满足以下两个条件：

互斥性：对于任意 $i \neq j$（$i, j = 1, 2, \ldots, n$），有 $B_i \cap B_j = \emptyset$，即事件两两互不重叠。
完备性：所有事件的并集覆盖整个样本空间，即 $\bigcup_{i=1}^{n} B_i = S$。

意义：划分确保了样本空间中的每个可能 outcome 都恰好属于一个事件 $B_i$，这==使得概率计算可以分解为对这些互斥部分的和==。例如，在全概率公式中，如果 $A$ 是任意事件，则 $P(A) = \sum_{i=1}^{n} P(A \mid B_i) P(B_i)$，前提是 $B_i$ 形成一个划分。

示例：假设样本空间 $S$ 表示掷一个公平六面骰子的结果，即 $S = \{1, 2, 3, 4, 5, 6\}$。定义事件 $B_1 = \{1, 2\}$, $B_2 = \{3, 4\}$, $B_3 = \{5, 6\}$。这些事件满足： - 互斥性：$B_i \cap B_j = \emptyset$ 对于 $i \neq j$。 - 完备性：$B_1 \cup B_2 \cup B_3 = S$。

因此，$B_1, B_2, B_3$ 是 $S$ 的一个划分。

推导⚓︎

全概率公式是概率论中的重要工具，用于计算事件 $A$ 的概率，当样本空间 $S$ 被划分为互斥且完备的事件组 $B_1, B_2, \ldots, B_n$ 时。公式如下：

\[ P(A) = \sum_{i=1}^{n} P(B_i) P(A \mid B_i) \]

推导过程

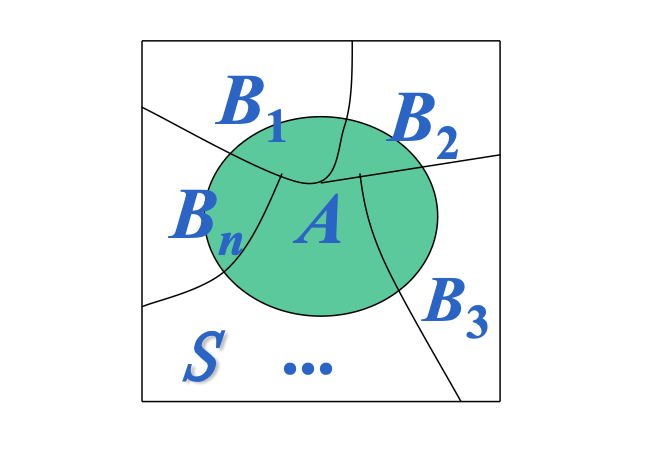
事件分解：由于 $B_1, B_2, \ldots, B_n$ 构成样本空间 $S$ 的划分，有 $S = \bigcup_{i=1}^{n} B_i$ 且 $B_i \cap B_j = \varnothing$（$i \neq j$）。因此，事件 $A$ 可以表示为： $$ A = A \cap S = A \cap \left( \bigcup_{i=1}^{n} B_i \right) = \bigcup_{i=1}^{n} (A \cap B_i) $$
互斥性：由于 $B_i$ 互斥，事件 $A \cap B_i$ 也互斥，即 $(A \cap B_i) \cap (A \cap B_j) = \varnothing$ 对于 $i \neq j$。
概率可加性：根据概率的有限可加性，互斥事件的并集概率等于概率之和： $$ P(A) = P\left( \bigcup_{i=1}^{n} (A \cap B_i) \right) = \sum_{i=1}^{n} P(A \cap B_i) $$
乘法定理：利用条件概率公式 $P(A \cap B_i) = P(B_i) P(A \mid B_i)$，代入上式得： $$ P(A) = \sum_{i=1}^{n} P(B_i) P(A \mid B_i) $$

下面的韦恩图直观展示了这一推导：正方形代表样本空间 $S$，被分割成互斥区域 $B_1, B_2, \ldots$，绿色圆形代表事件 $A$，与各 $B_i$ 的交集 $A \cap B_i$ 即为概率求和的部分。

设$B_{1},B_{2},\cdots B_{n}$为S的一个划分，$P( B_{i} )>0,(i=1,2,\cdots,n)$,对 $E$的任一事件$A$,有

\[P(A)=\sum_{i=1}^{n} P(B_{i})P(A\mid B_{i}).\]

称上式为全概率公式.

贝叶斯公式⚓︎

若事件 $B_{1},B_{2},...,B_{n}$ 是引起事件 $A$ 发生的 $n$ 个原因，它们的概率 $P(B_{i})$ ($i=1,2,...,n$) 是在对 $A$ 观察前就已知的，因此通常叫做先验概率。

如果在一次试验中，事件 $A$（结果）发生了，那么反过来：$A$ 的发生是由第 $i$ 个原因引起的概率 $P(B_{i}|A)$ 是多少?这就是贝叶斯公式解决的问题。通常称 $P(B_{i}|A)$ ($i=1,2,...,n$) 为后验概率。

全概率公式是“由因导果”的一个过程，贝叶斯公式则是“由果溯因”的一个推断公式。

\[ P\left(B_{i}\mid A\right)=\frac{P\left(B_{i}\right) P\left(A\mid B_{i}\right)}{\sum_{j=1}^{n} P\left(B_{j}\right) P\left(A\mid B_{j}\right)} \]