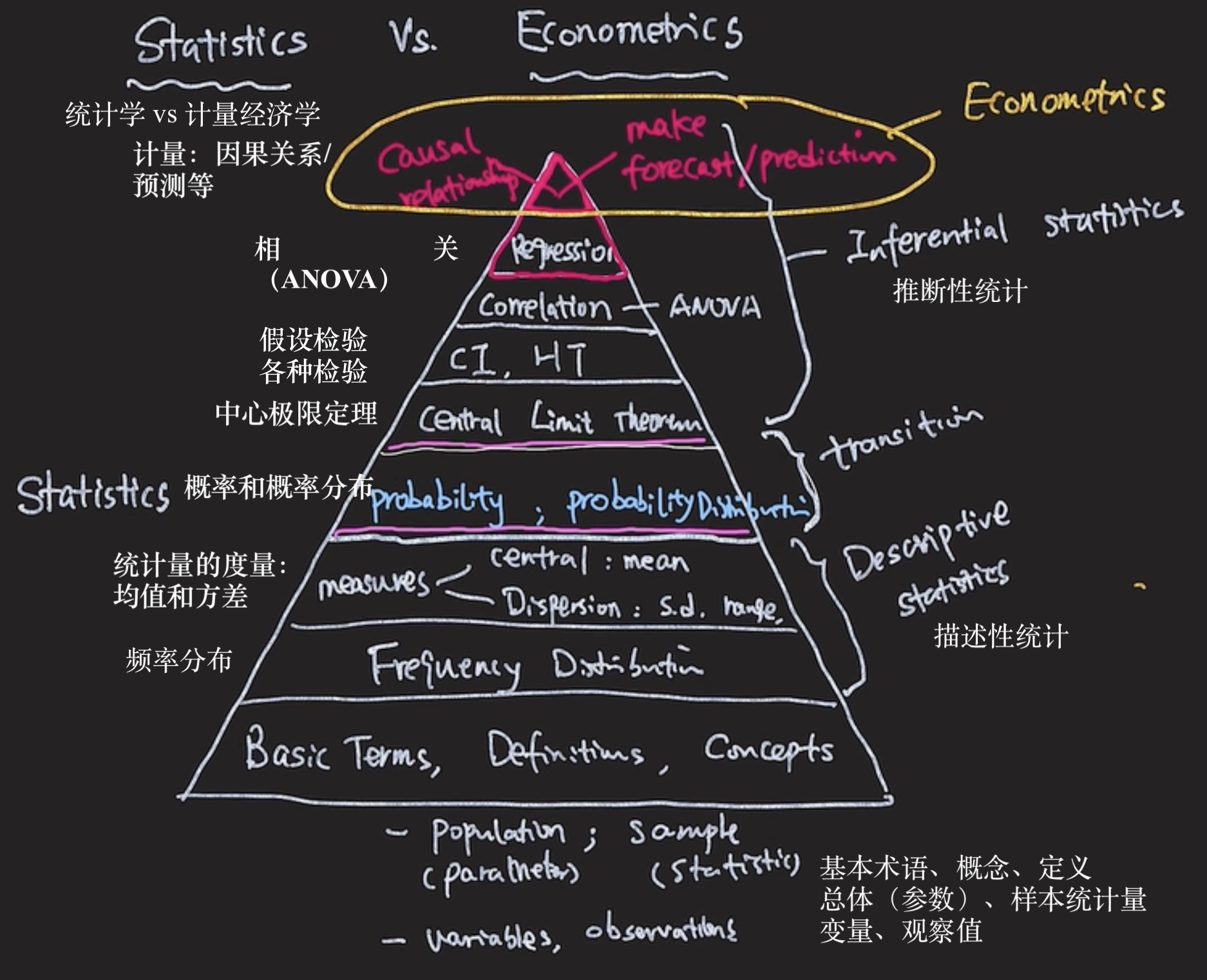
统计学方法⚓︎
约 2070 个字 3 张图片 预计阅读时间 7 分钟 总阅读量 次
假设检验⚓︎
- Null hypothesis
- 为什么一定在原假设上放等号:因为总要放入一个定值来(和样本/抽样)确定和比较
- P-value的含义:就是假定原假设是真的,真实情况比样本测出来的情况相等或者更加more extreme的概率。
方差分析 ANOVA⚓︎
Analysis of Variance
- H_0 : \mu_ 1 = \mu_2 = \mu_3
-
H_1 : At least one \mu is different
-
e.g. Professor rating (X) with Students' score(Y)
- 他们的 \(\mu\) 是否是相同的?如果相同(接受原假设),说明是否喜欢老师与最终的学生分数无关。(X和Y之间没有关系)
- 做法:
- 全Y的方差由:X的方差和组内误差方差解释;如果X的方差解释比误差方差的影响还要小,说明是否喜欢老师与分数无关;
- 组间误差是否比组内误差小;
F分布⚓︎
- F 检验:样本标准差的平方,两组数据可以得到两个平方,用X的方差去除以误差的方差(注意下自由度的问题),计算出F的值,就是方差的商
- variation explained by X;
- variation explained by errors;
- \(F = \dfrac{S^{2}_{1}}{S^{2}_{2}}\)
- 自由度(见下面一个专题)
- MS:mean square
自由度⚓︎
- 自由度(Degrees of Freedom)
一种便于计算统计量的解释(statistical measures)⚓︎
- 经典的“你为什么要n-1!”
-
Population(总量N)
- E(X) = \dfrac{}{}, 总体参数(parameter)
- \(\sigma^{2}(x) = \dfrac{}{}\)
-
Sample:
- 样本,总量\(n\) ,样本统计量:
- \(\bar{x}\) (x bar)表示样本期望;
- \(S^{2} (x) = \dfrac{\sum (x_i - \bar{x})^2 }{n - 1}\),这里的 n - 1就是自由度;为什么这里的样本方差会和总体方差不同呢?
- 我们计算这些样本的统计量,实际上是为了估计(estimate)总体的统计量的,我们大多数时候并不知道总体的情况如何;
- 我们可以采样!一个采样形成一个点估计。样本的方差正是用来估计总体方差的。
- 问题出现了,如果样本的方差选择用 n 而不是 n - 1,我们常常会低估(underestimate) 总体的方差的真值;如果用 n - 1 就可以纠正这个错误,更加接近真实值;
- Def: The number of free-moving observations / elements.
- 对于总体来说,可以有\(N\)个取值;自由度是\(N\),但是如果我们从中取样之后,计算出给定样本的均值之后,\(\dfrac{x_1 + x_2 + x_3}{3} = \bar{x}\), 实际上只有\(n - 1\)个值是“自由”的,因为无论选择哪个数,都可以被这\(n - 1\)个数线性表示了。另一个角度说,当样本很大很大( n \to \infty ),N 约等于 N - 1了,严格意义上,此时也不需要考虑自由度了,因为样本就已经变成了整体。
- ❓那么为什么,在计算均值的时候为什么不需要加上 n - 1: 此时没有任何限制;因为只是一个样本,它确实有n个“自由”的样本个体,所以均值依然是 n 。简单来说,只要你知道了一个样本某类型的均值,那么你就丢失了一个自由度。
一种基于回归分析的解释⚓︎
- \(y = b_0 + b_1 x + \mu_i\)
- OLS。先画个散点图。
- 如果想要求\(b_0, b_1\),那么我们最少需要几个观测值才能求出这两个值?
- 至少需要两个点(不然连不成一个直线)
- 但是,如果只有两个点,此时这两个点都不是“自由”的,因为当且仅当有了这两个点才能确定这个线,这时候其实不是预测,而是“确定”,根本不需要评估关系强度如何(因为你已经具体确定了)。此时的自由度是0。只有有了多于两个点,才能评估这种相关关系的强度(assess the strength of relationship)。这时候的自由度就是1.如果是 n = 4,那么自由度就是 2, 以此类推;也就是和独立变量的个数 x相关,(回归变量个数?number of regressors),\(d.f. = n - (k + 1)\)
- 如果我们有两个独立变量, \(y = b_0 + b_1 x_1 + b_2 x_2 + \mu\),此时是一个回归平面;此时需要的最少的样本数是3(抽象一下,如果只有两个点,连成一个线,那么有无数个面可以过这个线——除非你再确定一个点,让这个平面也过这个点,才能唯一确定一个平面;
- 拓展:回归分析中 \(R^2\) 情况的分析
大数定律⚓︎
- 大数定律是描述相当多次数重复实验的结果的定律。根据这个定律知道,样本数量越多,则其算术平均值就有越高的概率接近期望值。大数定律很重要,因为它“说明”了一些随机事件的均值的长期稳定性。人们发现,在重复试验中,随着试验次数的增加,事件发生的频率趋于一个稳定值;人们同时也发现,在对物理量的测量实践中,测定值的算术平均也具有稳定性。
中心极限定理⚓︎
- 当样本足够大的时候,样本的均值会服从正态分布。
- 是关于\(\bar{x}\)的,也就是从样本总体中抽样出一个样本量足够大的样本 ( n > 30 ),这些样本会有一个均值,这个值也是随机变量;这个变量也是服从正态分布的;
- 当总体样本服从均值为 \(\mu\), 标准差为 \(\sigma\) 的分布的时候,当n足够大时,样本均值服从均值为 \mu, 标准为 \(\sigma / \sqrt{n}\)的分布。\(n\)为样本容量;
- 我们同样把这时 \bar{x} 的标准差(也就是样本的均值的标准差)称作 标准误 (Standard error)
- 注意了样本标准差不叫标准误,就是标准差;
标准差和标准误的理解⚓︎
- 方差的作用是描述数据的分散程度(dispersion)
- 样本的方差要除以(n-1)
- 为什么有误差:
- 因为\bar{x}就是为了把它当作总体均值的点估计;
- 此时\bar{x}的标准差就是对整体均值偏离程度的一种点估计;
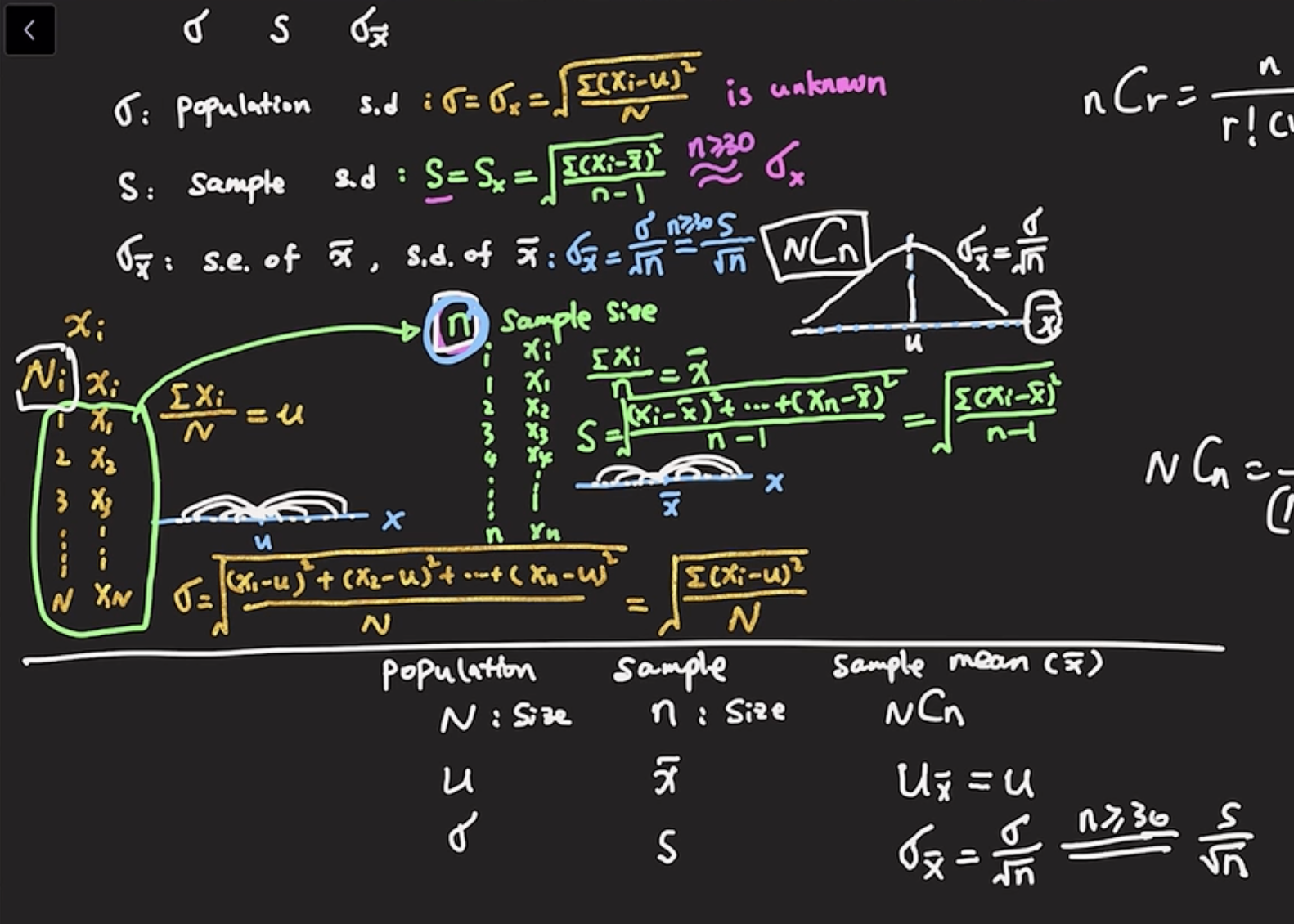
总体标准差 \(\sigma\) | 样本标准差 \(S\)| 样本的均值的标准差 \(\sigma_{\bar{x}}\)⚓︎
- 大部分时候的样本的参数都是不可知的,需要用样本的统计量来估计参数,所以,当样本的n足够大(>30)的时候,我们可以认为样本的均值近似于总体的均值;
- 我们就会用样本的均值来估计总体的均值;
- 样本均值的标准差 = 总体标准差 / \(\sqrt{}\)样本数量
- 样本的均值(这个随机变量)的个数是 \(C^{n}_{N}\)
- 当n足够大的时候我们获得了一种估计总体的方法,但是n如果不够大的时候,该怎么办?
t分布⚓︎
- 当总体服从正态分布(此时抽样样本服从正态分布),如果抽样的样本数小于30(是一个小样本)的话,此时样本均值的标准差不能用样本的标准差来近似了(不能用S来近似\sigma)。
z-score | z-分布⚓︎
- 说白了就是均值为0,方差为1的正态分布;
- \(\mu \pm 1.96 \times \dfrac{S}{\sqrt{n}}\)
- 在上面所述的情况中,不能用z分布的方法来进行计算了,因为我们不仅不知道总体的标准差,由于数量较小我们也不能用样本的标准差来近似样本均值的标准差;在这种情况下我们就需要用到t-分布;
- z-score的过程就是,我们首先给定了\(\alpha = 5\%\),对称的两边各分\(2.5\%\)。此时对应x轴上的数字是多少?怎么求?这个过程就是上面的\(\mu \pm 1.96 \times \dfrac{S}{\sqrt{n}}\)的过程
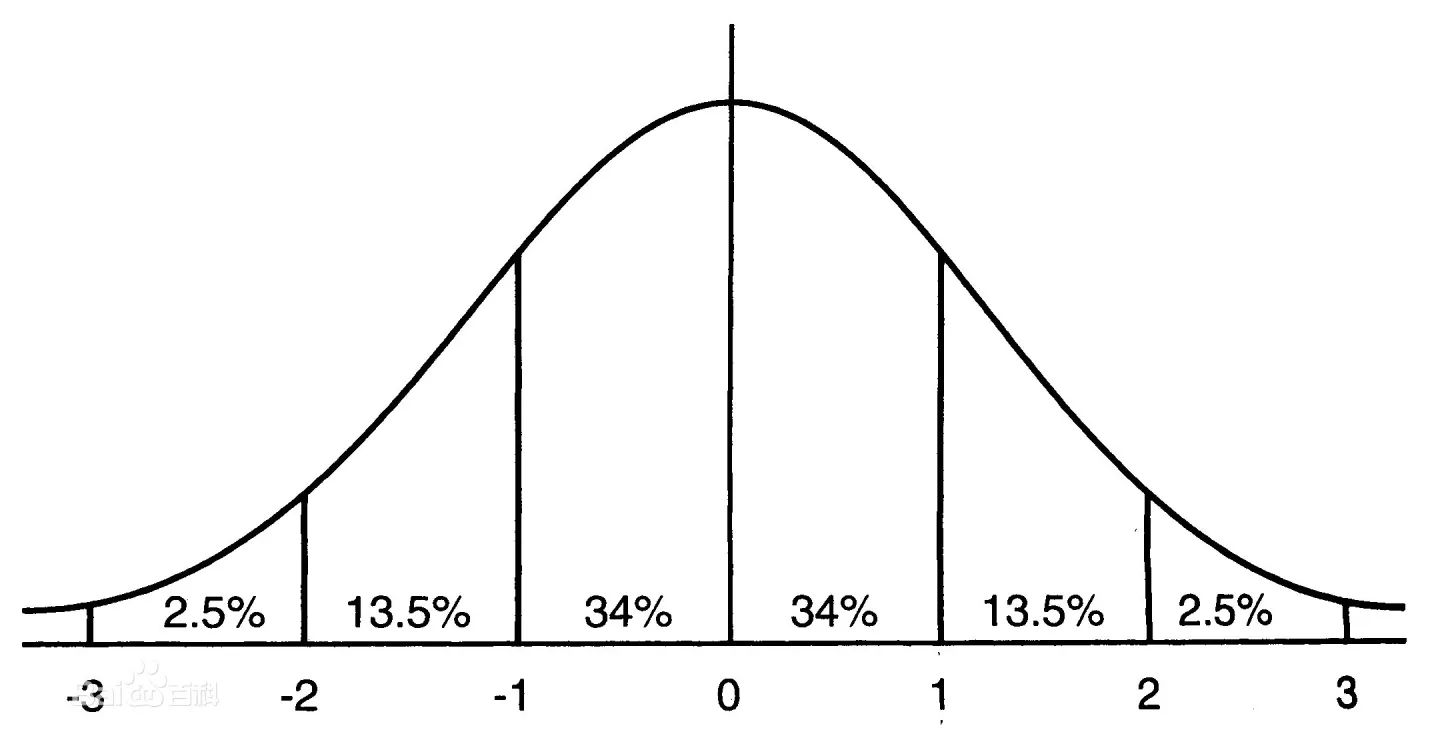
- 回到t分布上来,此时不能通过z-score的方法求解那个具体的数值了;
- t-distribution 均值是0,但是它的方差存在波动