经济订货批量模型⚓︎
约 1005 个字 1 张图片 预计阅读时间 3 分钟 总阅读量 次
模型建立⚓︎
-
在采购时,需要确定一份补货订单,采购批量为\(Q\)的物品,为了确定\(Q\)的具体数值,我们假设有以下的输入:
- \(D =\) 产品的年需求量
- \(S =\) 每次订货的固定成本
- \(C =\) 单位成本
- \(h =\) 年库存占有成本占产品成本的比率
-
假设供应商不提供折扣,无论订货规模多大,每单位物品的成本均为\(C\),此时库存持有成本是\(H = hc\),我们采用如下基本假设来构建模型。
- 单位时间内的需求稳定为\(D\)单位;
- 不允许出现短缺,也就是必须通过库存来供应所有需求
- 补货提前期是固定的(初始值为0)
-
为了最小化总成本,需要考虑如下三点:
- 年原材料成本 = \(CD\)
- 订货次数必须满足年需求量\(D\),给定订货批量\(Q\),我们有年订货次数 = \(\dfrac{D}{Q}\)
- 由于每次订货都会有订货成本\(S\),因此有,年订货成本 = \((\dfrac{D}{Q}) S\)
-
给定订货批量\(Q\),可以获得平均库存Q/2,因此年库存持有成本为持有Q/2单位库存一年的成本,也就是: 年库存持有成本 =
\[( \dfrac{Q}{2} ) H = (\dfrac{Q}{2} )hC\]
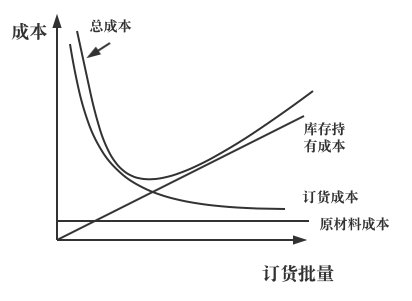
- 上面的成本总和
\[TC = CD + (\dfrac{D}{Q}) S + (\dfrac{Q}{2} )hC\]
- 就\(Q\)对总成本求一阶导数并令其为0,最优订货批量被称为经济订货批量(Economic Order Quantity, EOQ),用\(Q^{*}\)表示。公式为:
\[Q^{*} = \sqrt{\dfrac{2DS}{hC}}\]
- 对于上述公式,年库存持有成本比率\(h\)和需求\(D\)的时间应该保持一致,对于订货批量\(Q^{*}\),系统中的周转库存为\(Q^{*} /2\),单位产品在系统内的流动时间为\(Q^{*} / (2D)\),随着最优订货批量的增长,周转库存和流动时间也会增加,最优订货频率\(n^{*}\)为:
\[n^{*} = \dfrac{D}{Q^{*} } = \sqrt{\dfrac{DhC}{2S}}\]
案例分析⚓︎
A 公司对某电脑的需求为1000台,每次订购的固定成本、运输和收货成本为4000美元,每台电脑的价格是500美元。零售商库存持有成本是20%,计算商店经理每次订货应该订购多少电脑?
年需求 = 1000 \(\times\) 12 = 12000; 每批次订货成本\(S = 4000\),每台电脑的单位成本\(C\) = 500,h = 0.2,那么按照公式可以算出
\(Q^{*} =\sqrt{ \dfrac{2 * 12000 * 4000}{0.2 * 500} } = 980\)
此时的周转库存是980 /2 = 490
此时的年订货次数 = 12000 / 980 = 12.24
年订货成本+库存持有成本(套前面的公式) = 97980。
平均流动时间 = \(Q^{*} / (2D) = 490 / 12000 = 0.041\) Year
延伸⚓︎
-
如果我们把订货批量设置在1100单位(而不是980),此时的年成本会从97980增加到98636,虽然和最优订货批量相比,这个订单批量超过了10%,但是总成本仅增加了0.67%。在现实中可以这样理解:如果CD的经济订货批量是6.5个单位,制造商很可能不愿意运送半单位的货物从而提出收取额外费用,此时我们把批量适度增加,这种改变几乎不影响库存相关成本,但是可以节省制造商提供半箱货物运输而收取的额外费用。
-
要点✅ : 在经济订货批量附近,订货总成本和库存持有成本相对稳定,在很多时候订购一个接近经济订货批量的适当批量,比完全按照经济批量来更为划算
-
要点✅ : 如果需求增加\(k\)倍,那么最优订货批量将增加\(\sqrt{k}\)倍,年订货次数也增加\(\sqrt{k}\)倍,周转库存的流动时间则减少为原来的\(\dfrac{1}{ \sqrt{k} }\)
-
要点✅:如果想要把最优订货批量减少为原来的\(1/k\),那么固定订货成本必须减少为原来的\(1/ k^{2}\)
-