Truck and Drones⚓︎
约 2020 个字 14 张图片 预计阅读时间 7 分钟 总阅读量 次
调度模式
- 一辆车的情况:
-
货车-无人机协同调度(Collaborative,对应FSTSP)
飞机需要从车上起降,并且有相关运行约束;
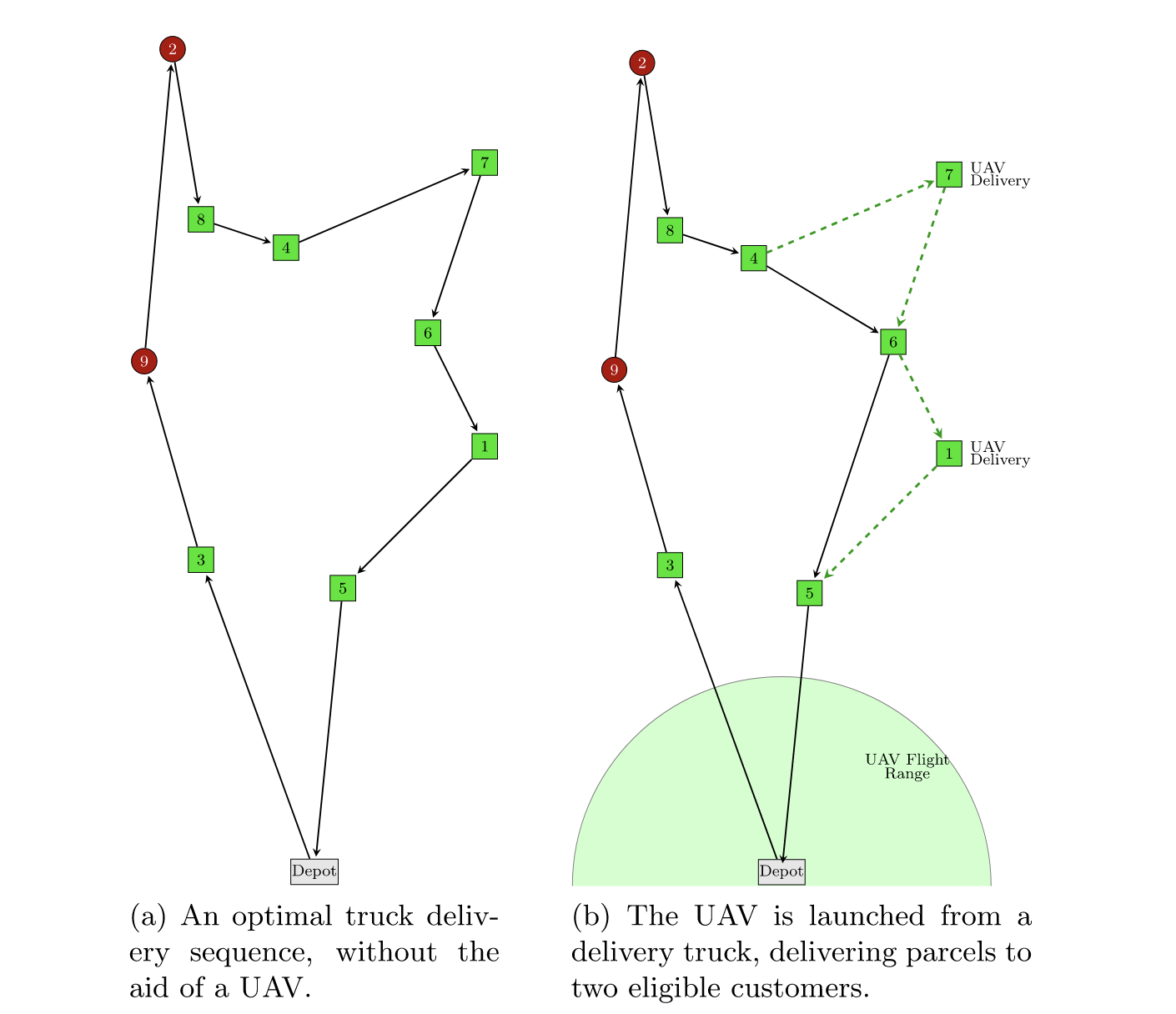
- 货车-无人机并行调度(Parallel, 对应PDSTSP):
同时运行,但是互不干扰;
FSTSP⚓︎
- \(x_{ij}\):卡车是否从 \(i\) 开往 \(j\) 点;
- \(y_{ijk}\): UAV是否从 \(i\) 起飞服务 \(j\) 地最后在 \(k\) 降落在卡车上。
- \(t_j\): 卡车到达 \(j\) 地的时间
- \(t_{j}^{'}\): UAV到达 \(j\) 地的时间
其他参数:
-
\(s_L, s_R\): 卡车成员释放无人机和回收无人机所需的时间
-
辅助决策变量: \(p_{ij}\) 顾客 \(i\) 在 \(j\) 之前被服务,则为1,目的是约束飞机的飞行要是连续的。 \(p_{0j} = 1\),约束起点必须是在所有顾客之前被访问。
-
辅助决策变量:\(1 \leq u_i \leq c + 2\) 。限制子环路。
每个飞机每次只能访问一个顾客。


Heuristic for FSTSP⚓︎
先假设所有的点都是卡车访问,然后对每个可以被飞机访问的节点,尝试分配给飞机,从卡车上起飞执行运输。

然后针对每个可以插入飞行的无人机节点,看看能否产生节约。


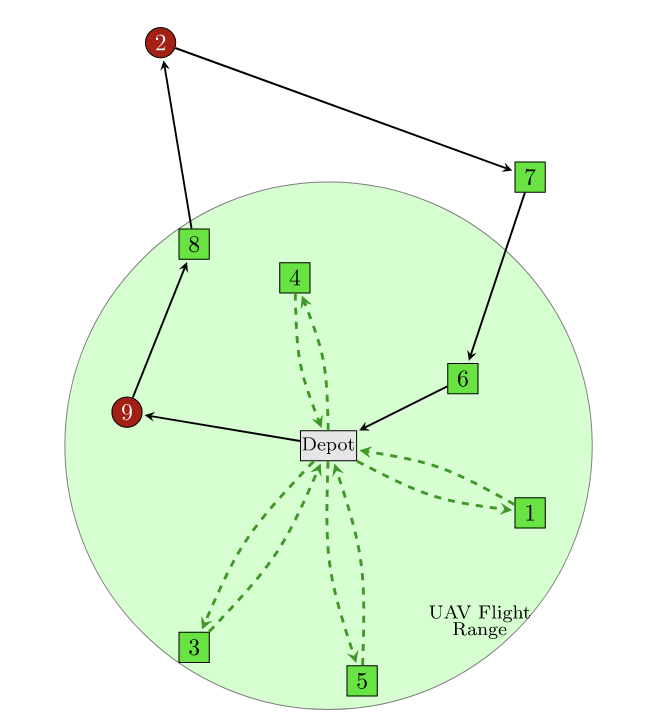
PDSTSP⚓︎
并行调度模式,UAV与卡车独立工作。因为无人机不局限在卡车上,所以无人机可以有很多个。卡车(在这个模型里)只有一个。Murray指出该问题实际上是两个经典问题的结合。TSP + PMS(Parallel Machine Scheduling), 首先对虽有需要卡车访问的地方,就是一个TSP问题,确保每个点可以访问,接下来给无人机访问的地方用并行机调度模型。
(Saleu et al., 2018) 改进了原本的启发式方法,可以求解229个客户点、多UAV的问题。
MBIADOU SALEU R G,DEROUSSI L,FEILLET D,et al. An Iterative Two-Step Heuristic for the Parallel Drone Scheduling Traveling Salesman Problem[J]. Networks,2018,72(04):459-474.
- \(x_{ij}\), 卡车从 \(i\) 开往 \(j\) 地;
- \(y_{j,v}\), 第 \(j\) 个顾客由第 \(v\) 个UAV服务;

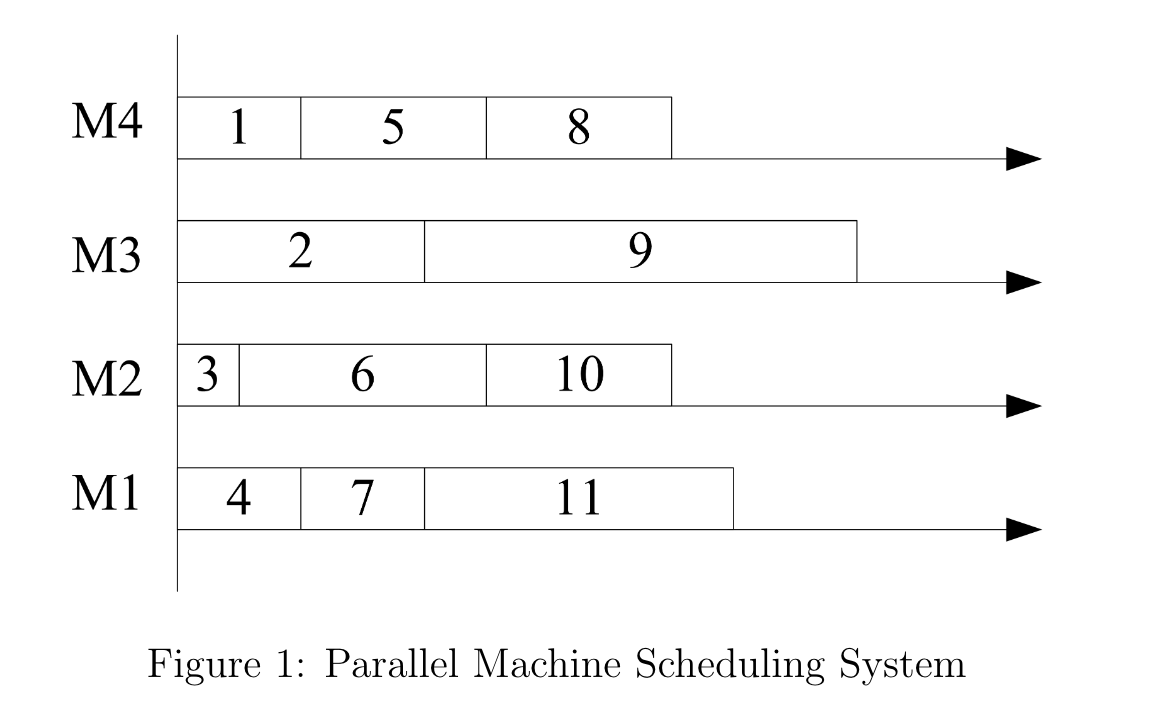
Here, each customer represents a ‘‘job’’ to be scheduled, the ‘‘processing time’’ of each being given by the UAV’s round trip flight time to serve that customer from the distribution center. PMS原本是需要把工作分配到机器上,决定该如何分配;现在把每个飞机视为一台机器,每个顾客视为一个工作。决定如何分配。工作结束时间就是每台机器加工完所有工作的结束时间。
Heuristic for PDSTSP (Murray & Chu, 2015)⚓︎
- 最开始,先假定所有的在UAV服务半径内可以被服务的顾客,全部安排给UAV去服务,那些不在服务区内的点就分配给车。一般而言,初始化后,车服务的顾客 <<< UAV的顾客。
如果UAV的MKspan > Truck 的MKspan:
把每个UAV的单派给Truck,看看两个方案的最晚时间是否有改进,如果有,Update;
- Swap 函数(实际是一个Operator算子):上述启发式后,把原来卡车的交给无人机去服务,原来无人机的交给卡车去服务:看看是否会有改进;
直到没有优化为止。
论文的数值实验:10~20个客户(小),大部分可被无人机访问;大部分节点都在UAV的可达范围内。 problems were generated with either 10 or 20 customers, such that 80–90% of customers were UAV-eligible. The truck and UAV speeds were fixed at 25 miles/h, the UAV having a flight endurance of 30 min. The depot location was selected as being either near the center of all customers, near the edge of the customer region, or at the origin (as with the FSTSP test problems). Customer locations were generated such that either 20%, 40%, 60%, or 80% of all customers were located within the UAV’s range of the depot. 两个节点之间的距离,对于卡车是曼哈顿距离,对于无人机,是欧氏距离。
PDTSP和FSTSP的结果对比:⚓︎
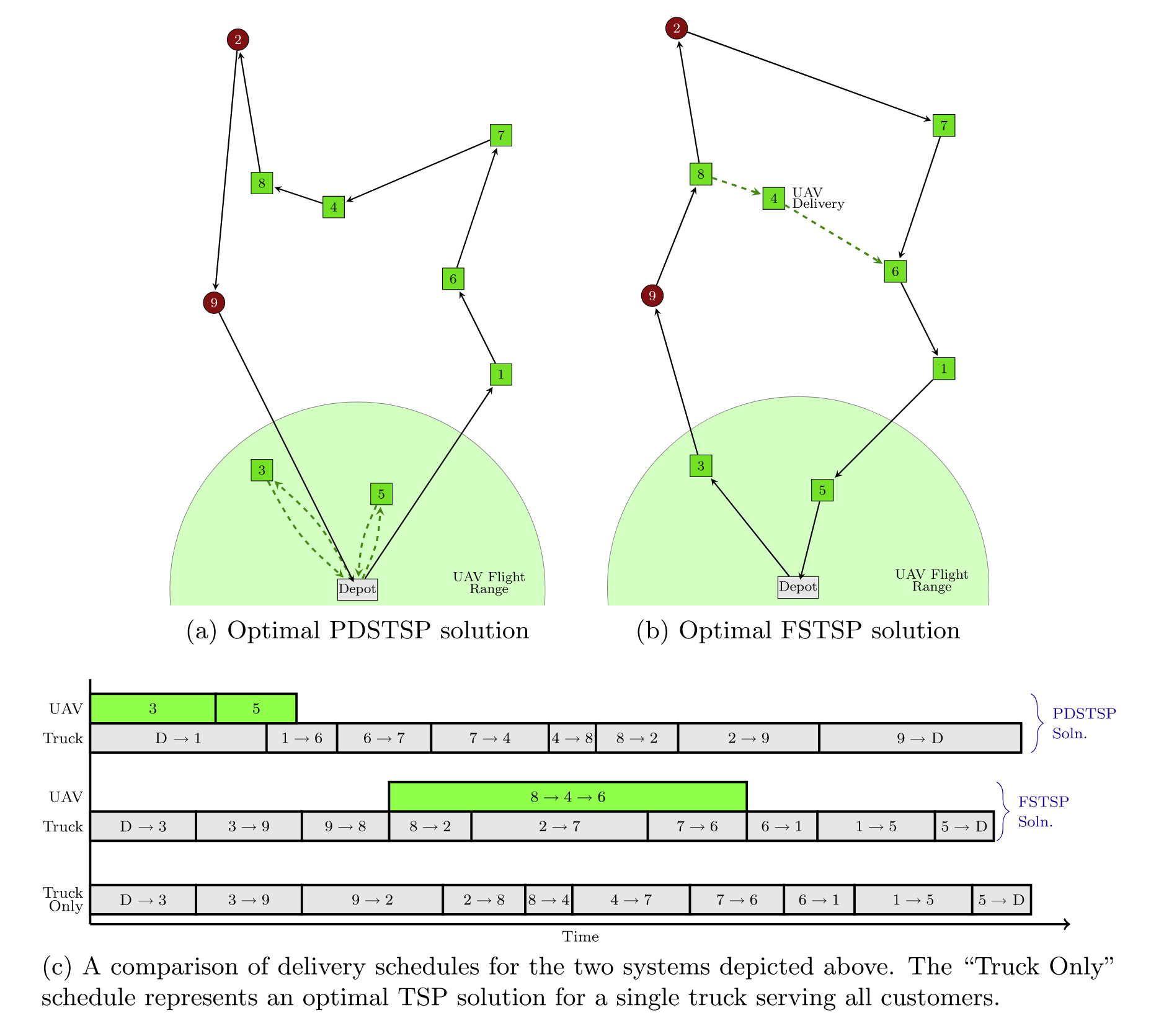
作者发现在小规模的场景下,FSTSP效果比PDSTSP要更好。
Heuristic for PDSTSP(ITERATIVE TWO-STEP HEURISTIC, 2018)⚓︎
Two-step 体现在整个问题的两个step:
- 把哪部分工作划分给哪部分交通工具?
- 划分完毕后,这部分(卡车/UAV)该怎么解决?

先假设所有的点都是由卡车访问的。生成TSP。把一部分订单拿出来给无人机执行。同时对删减后的TSP进行优化;对无人机的单用PMS进行优化。
- 这里需要回答一个问题:怎么划分这些订单呢?
只要新生成的解满足条件:
- 最迟的返回时间比原来的结果短
- 最迟返回时间不变,但,\(S_1, S_2\)的最小返回时间比 \(S^{'}_1, S^{'}_2\)的要大;
就可更新原来的解,然后继续尝试迭代了。
双标准最短路问题: Bicriteria shortest Path Problem。
并行机调度问题⚓︎
Parallel Machine Scheduling(PMS)并行机调度问题
存在多台相同或不同的机器可以同时处理任务。需要确定每个任务分配到哪台机器以及任务的处理顺序,以达到优化目标,如最小化完成所有任务的总时间或最大化产出等。
列生成求解:论文:Xu, J., Nagi, R., 2013. Identical parallel machine scheduling to minimise makespan and total weighted completion time: a column generation approach. Int. J. Prod. Res. 51 (23–24), 7091–7104.
目标函数:最小化加权完成时间的总和与总完工时间。这两个目标函数可以独立,也可以连在一起计算。PDTSP主要解决的问题是第二种场景,也就是仅仅最小化总的完工时间。
The objective function is to minimize the sum of the weighted completion time of every operation and weighted makespan.
\(N\) : 所有工作的集合; \(Y\) :机器的集合; \(w_j\) :工作j的权重; \(F_j\) :工作j的完成时间; \(F\):并行机排程问题的最大完成时间; \(B_j\) : 所有编号小于 \(j\) 的工作的集合;
决策变量:
\(x_{iy}\), 工作 \(i\) 是否分配给机器 \(y\), \(\forall i \in N, y \in Y\)
\(a_{ijy}\), 工作 \(i\) 和 \(j\) 是否同时被分配给机器 \(y\) ;\(\forall i \in B_j, j \in N, y \in Y\)
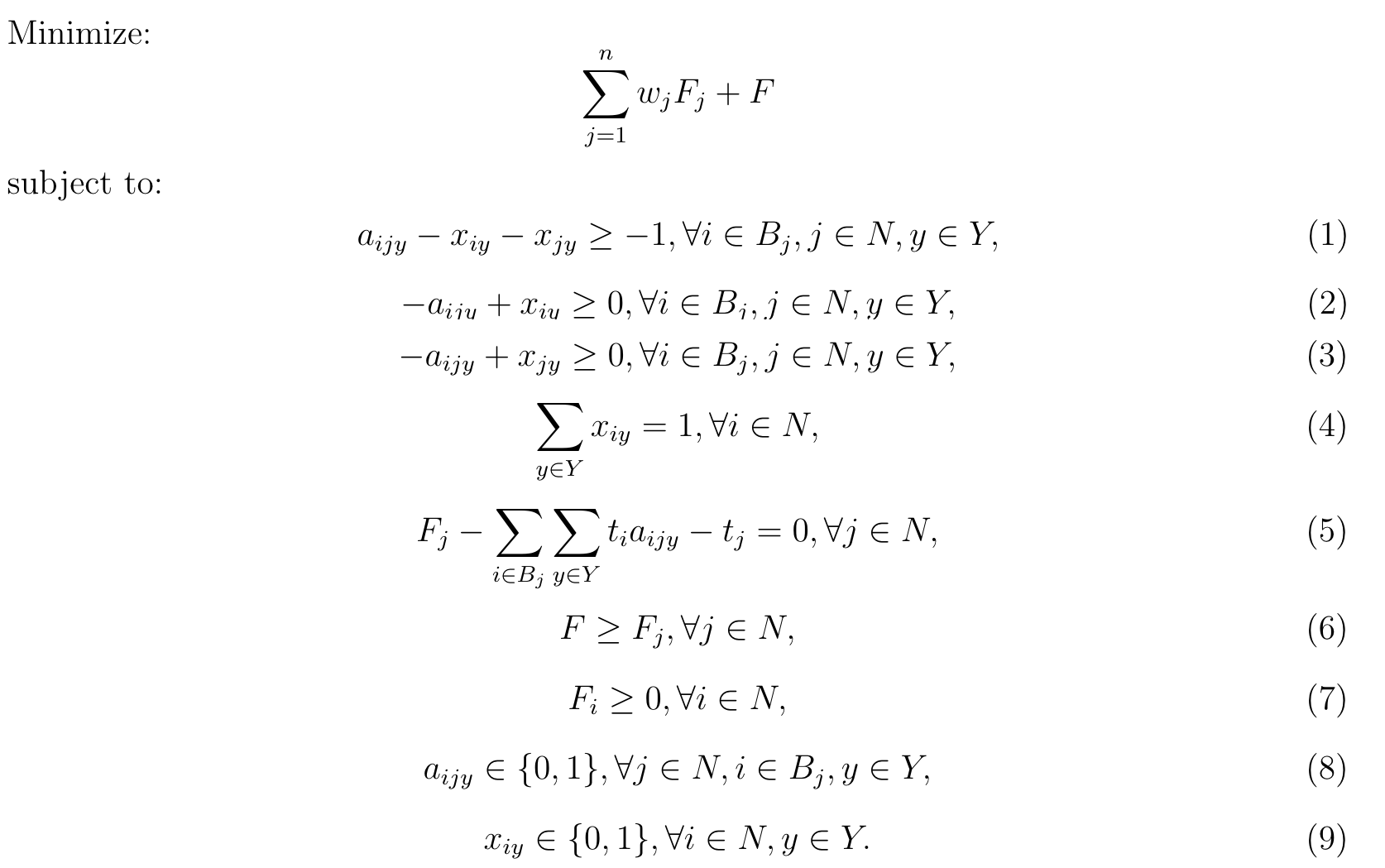
(1.2.3). 表示不同工作在机器上的分配情况;
(4). 每个任务只能被分到一个机器上;
(5). 计算总的完成时间;
(6). 约束每个任务的完成时间不早于最晚完成时间;
主问题,是在许多个“排班方案”里选择一部分,从而达到最优。
- \(s\): 列的序号;
- \(S\):列的标号的集合;
-
\(F^s\) : 该列任务所需的时间;
-
\(X_{iys}\) : 任务 \(i\) 是否被分给 \(y\) 机器,并采用 \(s\) 列的工序安排;这个值是子问题产生的一个常量。
-
\(Z_s\): \(s\)列是否被选作一个解;
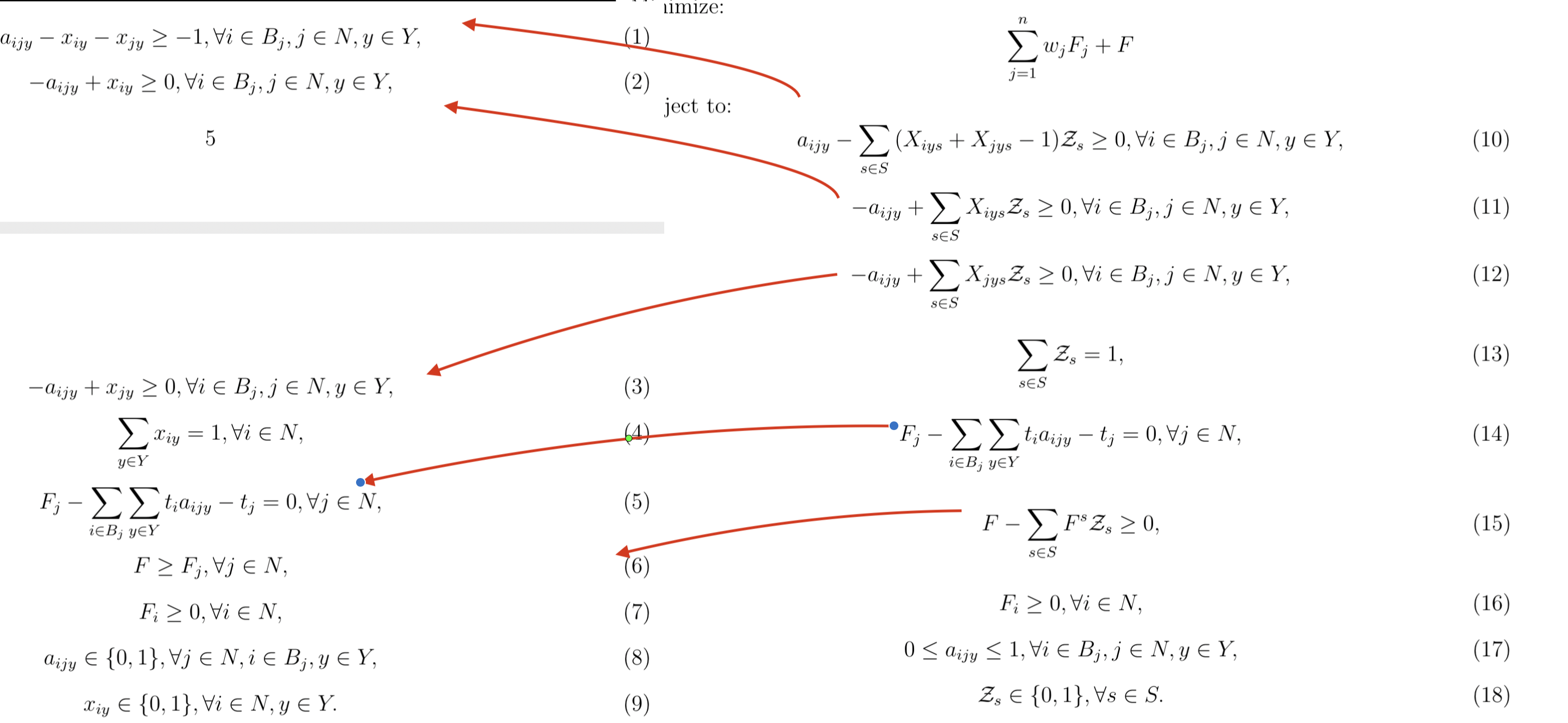
主问题与原问题的对应
子问题转化成“生成主问题的一列”,使得这一列的检验数(reduced cost)是负的。这样把这列加入主问题一定可以让主问题更优。
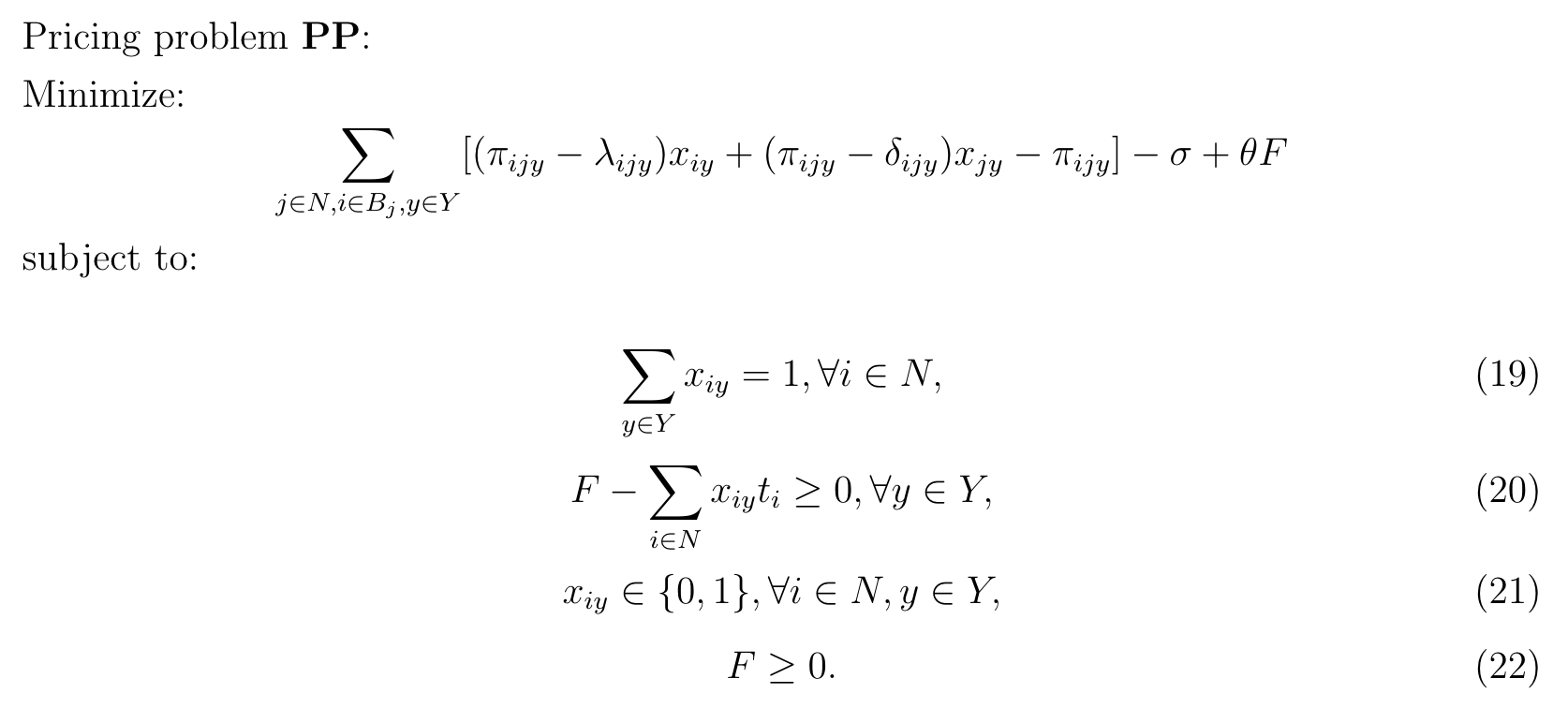
特定的应用:Bus-Drones Collaborative
- H同学的汇报:充电策略定价,需要补充UE相关的内容;
- G同学的汇报:V2G
- S同学的汇报:?
- Y同学的汇报:采样、随机森林
- 导师的总结:交通电力耦合网络均衡。每个人都可以做做试试看。求解算法的讨论。
- 最优路径生成的方法:基础、算法;
- 电力最优潮流问题;二阶锥规划;了解一下求解包的使用;
-
新型电力系统;混合整数规划的问题
- 仿真优化
-
固定时间在周五上午,每次两个同学。一个同学1h左右;3周轮一次。每次不一定是论文的分享。也可以是一些方法的层面:实现;
- 最优潮流、鲁棒优化;
- 每个部分也可以分成几个部分来做;一个人就围绕一个问题,每次讲一部分;
聚焦一个主题;不一定是一次性讲完;
- 交通网络均衡:H同学为主,Y参与;
- 仿真优化:Y同学,SUMO等;
- 鲁棒优化:G同学;
- 整数规划算法:我!S同学:了解了解;